直观理解反向传播法
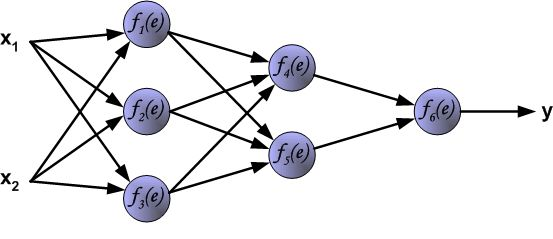

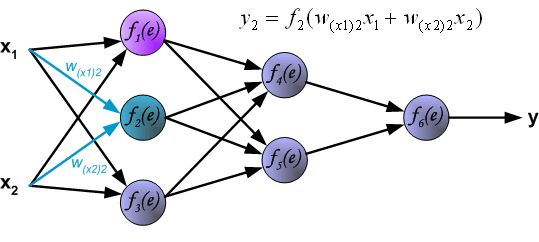
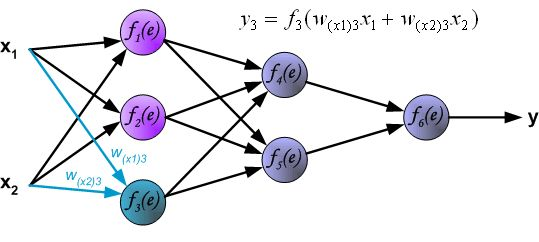
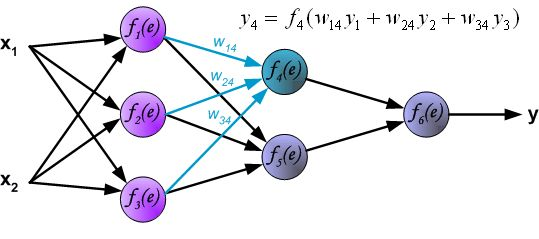
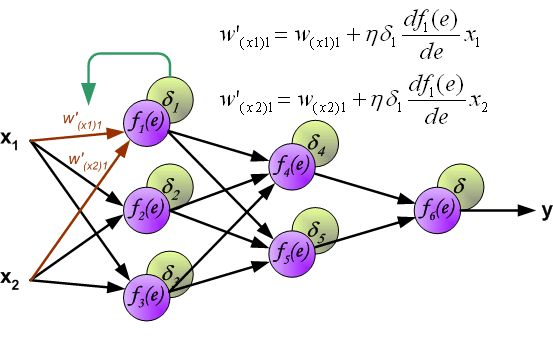
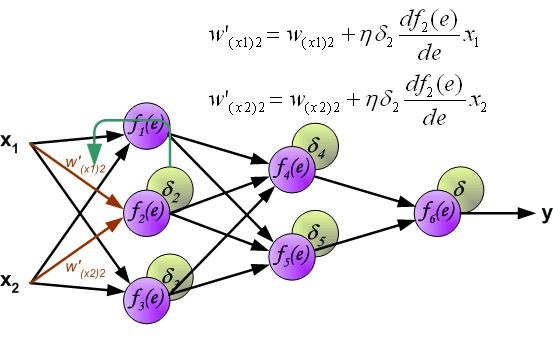
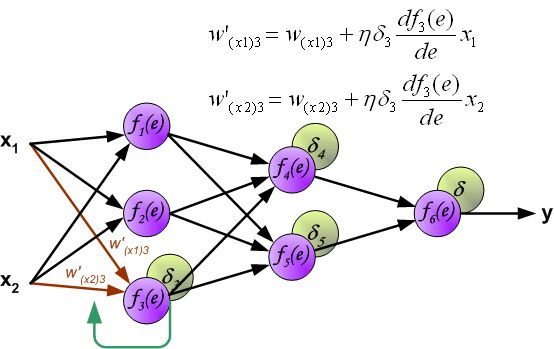
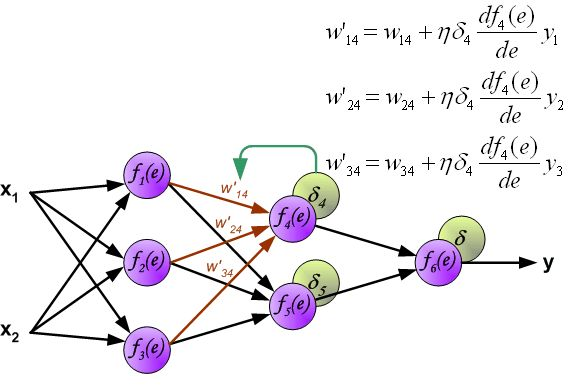
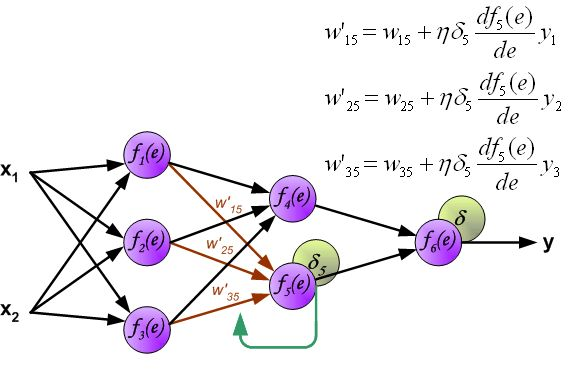
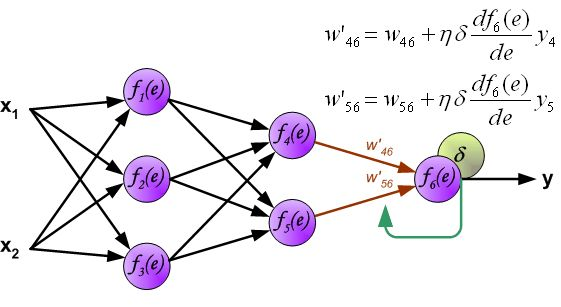
反向传播算法其实就是链式求导法则的应用。按照机器学习的通用套路,我们先确定神经网络的目标函数,然后用随机梯度下降优化算法去求目标函数最小值时的参数值。
反向传播算法
损失函数与正则化项
假设我们有一个固定样本集({(x^{(1)},y^{(1)}),···,(x^{(m)},y^{(m)})})它包含m个样本。我们可以用批量梯度下降法来求解神经网络。具体来讲,对于单个样例(x,y),其代价函数为:$$J(W,b;x,y)=frac{1}{2}||h_{W,b}{(x)}-y||^2$$
这是一个平方误差损失函数。(这里的(frac{1}{2})是当求导时,平方会产生一个2,(frac{1}{2}*2=1)进行平均不让2累积)
对于包含m个样本的数据集,我们可以定义整体的损失函数为:$$Jleft(W,b
ight)=left[frac{1}{m}sum_{i=1}^m{Jleft(W,b;x^{left(i
ight)},y^{left(j
ight)}
ight)}
ight]+frac{lambda}{2}sum_{l=1}^{n_l-1}{sum_{i=1}^{s_l}{sum_{j=1}^{s_{l+1}}{left(W_{ji}^{left(l
ight)}
ight)^2}}} =left[frac{1}{m}sum_{i=1}^m{frac{1}{2}}parallel h_{W,b}left(x^{left(i
ight)}
ight)-y^{left(i
ight)}parallel^2
ight]+frac{lambda}{2}sum_{l=1}^{n_l-1}{sum_{i=1}^{s_l}{sum_{j=1}^{s_{l+1}}{left(W_{ij}^{left(l
ight)}
ight)^2}}}$$
以上关于(J(W,b))定义中的第一项是均方误差项,第二项是一个正则化项,也叫权重衰减项,其目的就是减小权重的幅度,防止过度拟合。权重衰减参数λ用于控制公式中两项的相对重要性。(关于权重衰减部分,写在文尾)
算法讲解
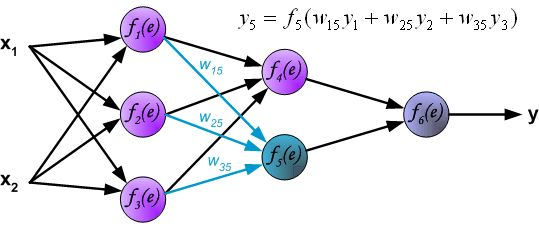
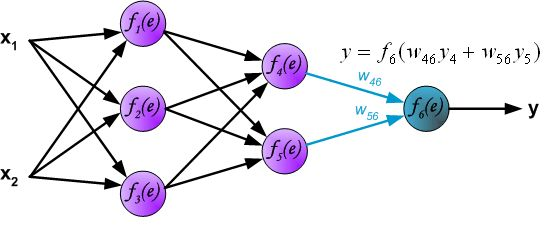
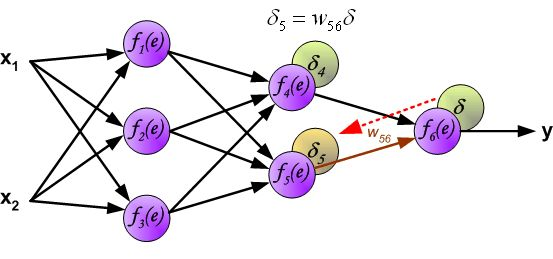
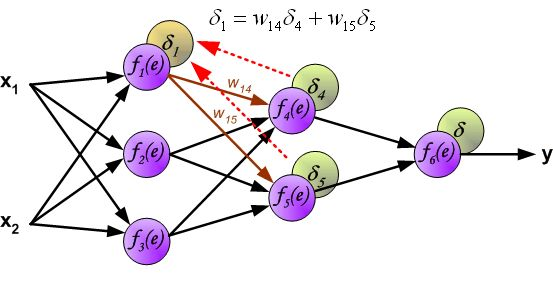
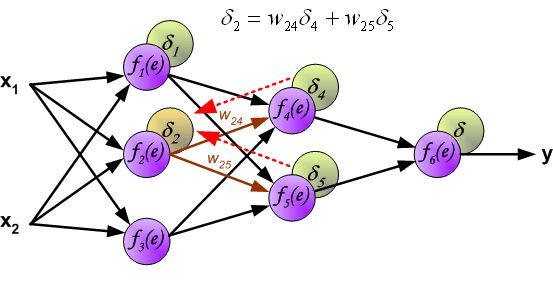
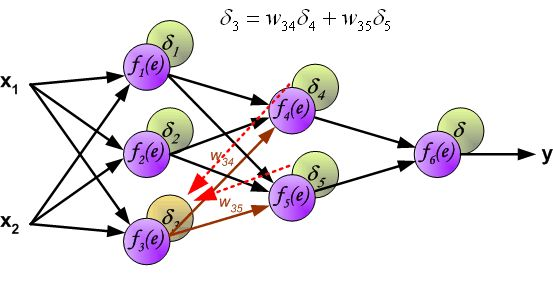
链式法则,具体如下图所示:
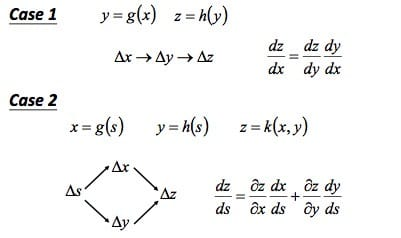
我们定义整体损失函数为:$$Lleft( heta
ight)=sum_{n=1}^N{C^nleft( heta
ight)}$$
对参数(w)求偏导:$$frac{partial Lleft( heta
ight)}{partial w}=sum_{n=1}^N{frac{partial C^nleft( heta
ight)}{partial w}}$$
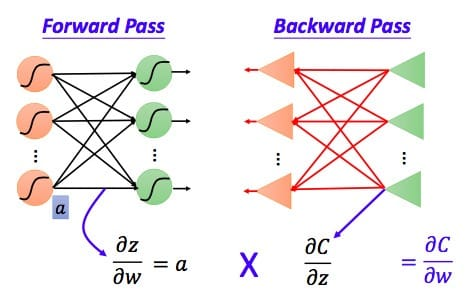
因此我们只需要求出单个样例的偏导数,就可以推导出整体损失函数的偏导数。根据链式法则,对于某一个节点,如下所示:
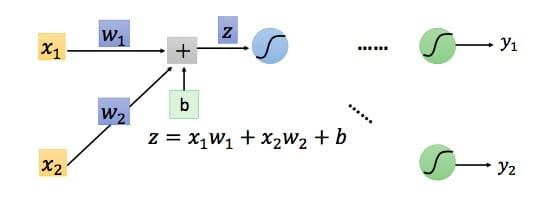
容易得到(partial z/partial w_1=x_1 qquad partial z/partial w_2=x_2)
我们可以利用前向传导的方法计算出所有层的(frac{partial z} {partial w})
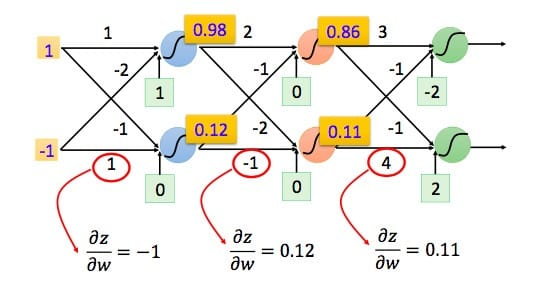
我们已经求出了整个偏导数的左半部分,接下来看右半部分,即(frac{partial C}{partial z})
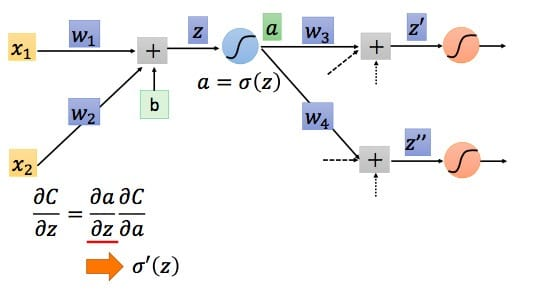
根据链式法则得到:$$frac{partial C}{partial z}=frac{partial a}{partial z}frac{partial C}{partial a}$$
对于(frac{partial a}{partial z}),我们知道就是激活函数对加法器的偏导,知道了激活函数便知道了(frac{partial a}{partial z}),我们设其求导结果为(partial ' (z)),因为z在前向传播中已经确定,所以(partial ' (z))其实是一个常数。接下来看(frac{partial C}{partial a}).
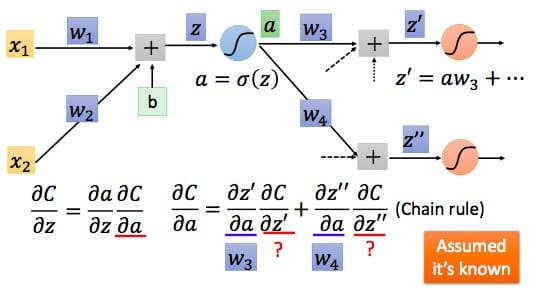
根据链式求导法则$$frac{partial C}{partial a}=frac{partial z'}{partial a}frac{partial C}{partial z'}+frac{partial z''}{partial a}frac{partial C}{partial z''}$$
易知(frac{partial z’}{partial a})即为权值,而(frac{partial C}{partial z’})假设其已知,则我们可以得到$$frac{partial C}{partial z}=sigma 'left(z
ight)left[w_3frac{partial C}{partial z'}+w_4frac{partial C}{partial z''}
ight]$$
而对于(frac{partial C}{partial z})的求导,我们需要区分输出层和隐藏层两种情况:
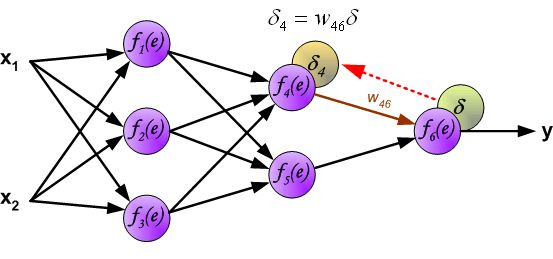
第一种情况,如果还处于隐藏层,我们可以根据上述算法不断递归的计算(frac{partial C}{partial z}),直到抵达输出层。
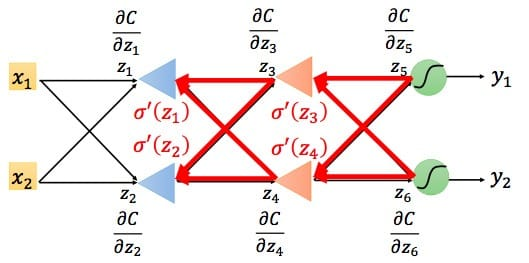
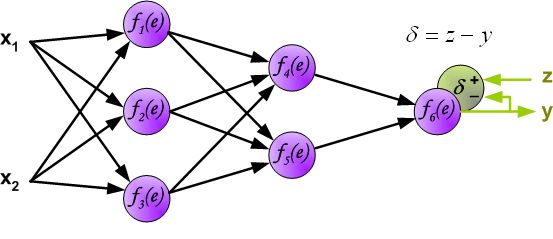
第二种情况,如果已经是输出层了,如下图所示
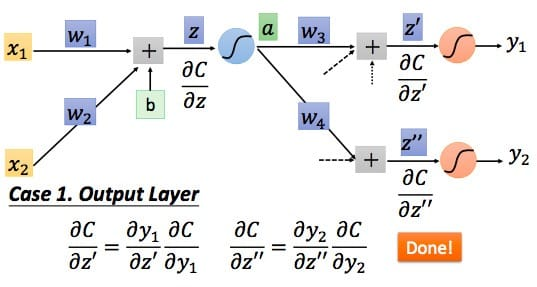
最后总结一下,我们根据前向传播算法求得所有的(frac{partial z}{partial w}),根据反向传播算法求得所有的(frac{partial C}{partial z})(需要用到前向传播算法求得的(frac{partial a}{partial z}),即(sigma ' left(z
ight)))。这样就可以用更新公式对参数进行迭代更新了。
权重衰减
目的:让权重衰减到更小的值,在一定程度上减少模型过拟合的问题。权重衰减也叫L2正则化。
L2正则化就是在代价函数后面再加上一个正则化项:$$C = C_0+frac{lambda}{2n}underset{w}sum w^2$$
其中C0代表原始的代价函数,后面那一项就是L2正则化项,它是这样来的:所有参数w的平方的和,除以训练集的样本大小n。λ就是正则项系数,权衡正则项与C0项的比重。另外还有一个系数1/2,1/2经常会看到,主要是为了后面求导的结果方便,后面那一项求导会产生一个2,与1/2相乘刚好凑整为1。系数λ就是权重衰减系数。
我们对加入L2正则化后的代价函数进行推导,先求导:$$frac{partial C}{partial w} = frac{partial C_0}{partial w}+frac{lambda}{n}w frac{partial C}{partial b} = frac{partial C_0}{partial b}$$
可以发现L2正则化项对b的更新没有影响,但是对于w的更新有影响:$$w
ightarrow w-etafrac{partial C_0}{partial w} - frac{eta lambda}{n}w =(1-frac{eta lambda}{n})w-etafrac{partial C_0}{partial w}$$
(eta)为学习率,学习率是梯度下降时控制我们每次靠近真实值的幅度。在不使用L2正则化时,求导结果中w前系数为1。现在w前面系数为(1-frac{eta lambda}{n}),因为(eta,lambda,n)都为正,所以(1-frac{eta lambda}{n})小于1,效果是减小w,这也就是权重衰减(weight decay)的由来。当然考虑到后面的导数项,w最终的值可能增大也可能减小。
对于基于mini-batch的随机梯度下降,w和b更新的公式跟上面给出的有点不同:$$w
ightarrow (1-frac{eta lambda}{n})w-frac{eta}{m}underset{x}sumfrac{partial C_x}{partial w} b
ightarrow b-frac{eta}{m}underset{x}sumfrac{partial C_x}{partial w}$$
对比上面w的更新公式,可以发现后面那一项变了,变成所有导数加和,乘以η再除以m,m是一个mini-batch中样本的个数。
思考:L2正则化项有让w变小的效果,但是为什么w变小可以防止过拟合呢?
原理:1. 从模型的复杂度上解释:更小的权值w,从某种意义上说,表示网络的复杂度更低,对数据的拟合更好(这个法则也叫做奥卡姆剃刀),而在实际应用中,也验证了这一点,L2正则化的效果往往好于未经正则化的效果。
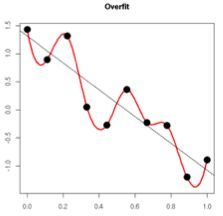
2. 从数学方面的解释:过拟合的时候,拟合函数的系数往往非常大,为什么?如下图所示,过拟合,就是拟合函数需要顾忌每一个点,最终形成的拟合函数波动很大。在某些很小的区间里,函数值的变化很剧烈。这就意味着函数在某些小区间里的导数值(绝对值)非常大,由于自变量值可大可小,所以只有系数足够大,才能保证导数值很大。而正则化是通过约束参数的范数使其不要太大,所以可以在一定程度上减少过拟合情况。
学习率衰减(learning rate decay)
在训练模型的时候,通常会遇到这种情况:我们平衡模型的训练速度和损失(loss)后选择了相对合适的学习率(learning rate),但是训练集的损失下降到一定的程度后就不在下降了。遇到这种情况通常可以通过适当降低学习率(learning rate)来实现。但是,降低学习率又会延长训练所需的时间。
学习率衰减(learning rate decay)就是一种可以平衡这两者之间矛盾的解决方案。学习率衰减的基本思想是:学习率随着训练的进行逐渐衰减。
学习率衰减基本有两种实现方法:
- 线性衰减。例如:每过5个epochs学习率减半。
- 指数衰减。例如:随着迭代轮数的增加学习率自动发生衰减,每过5个epochs将学习率乘以0.9998。(decayed_learning_rate=learning_rate*decay_rate^(global_step/decay_steps)),其中decayed_learning_rate为每一轮优化时使用的学习率,learning_rate为事先设定的初始学习率,decay_rate为衰减系数,decay_steps为衰减速度。
引用: