转载自:墨卡托投影实现 ,墨卡托投影,WGS84坐标与web墨卡托投影坐标转换
1.墨卡托投影:
又称正轴等角圆柱投影,由荷兰地图学家墨卡托(G.Mercator)于1569年创拟。假设地球被套在一个圆柱中,赤道与圆柱相切,然后在地球中心放一盏灯,把球面上的图形投影到圆柱体上,再把圆柱体展开,就形成以一幅墨卡托投影的世界地图(如下图)。因其等角特性,广泛应用与航空、航海中。
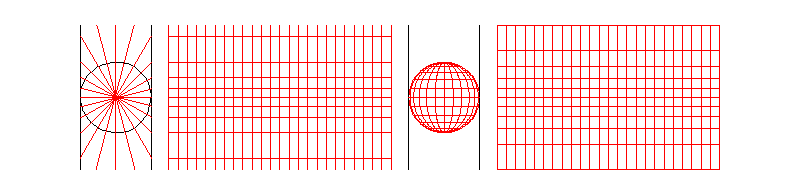
公式参数:
- a——椭球体长半轴
- b——椭球体短半轴
- f——扁率 ((a-b)/a)
- e——第一偏心率 (e=sqrt{1-(b/a)^2})
- e'——第二偏心率 (e=sqrt{(a/b)^2-1})
- N——卯酉圈曲率半径 (frac{a^2/b}{sqrt{1+e'^2*cos^2B}})
- R——子午圈曲率半径 (frac{a(1-e^2)}{(1-e^2*sin^2B)^{3/2}})
- B——纬度
- L——经度(单位rad)
- (X_N)——纵直角坐标
- (Y_E)——横直角坐标,单位米(M)
2.椭球体参数:
WGS84参数:长半轴:6378137;短半轴:6356752.3142
3.墨卡托投影正反解公式
墨卡托投影正解公式:(B,L)→(X,Y),标准纬度(B_0),原点纬度 0,原点经度(L_0)
[X_N = Kln[tg(frac{pi}{4}+frac{B}{2})*(frac{1-esinB}{1+esinB})^{e/2}]
]
[Y_E = K(L-L_0)
]
[K=N_{B_0}*cos(B_0)=frac{a^2/b}{sqrt{1+e'^2*cos^2{B_0}}}*cos{B_0}
]
墨卡托投影反解公式:(X,Y) →(B,L),标准纬度(B_0),原点纬度 0,原点经度(L_0)
[B=frac{pi}{2}-2arctg(EXP(-frac{X_N}{K})*EXP^{(frac{e}{2})ln(frac{1-esinB}{1+esinB})})
]
[L=frac{Y_E}{K}+L_0
]
P.S.公式中EXP 为自然对数底,纬度B 通过迭代计算很快就收敛了。
4.WGS84坐标与web墨卡托投影坐标转换
//把地球视为球体实现经纬度和墨卡托投影的函数
typedef struct Point
{
double x;
double y;
}WayPoint;
//经纬度转墨卡托
WayPoint lonLat2Mercator(WayPoint lonLat)
{
WayPoint mercator;
double x = lonLat.x * 20037508.34 / 180;
double y = log(tan((90 + lonLat.y) * Pi / 360))/(Pi / 180);
y = y * 20037508.34 / 180;
mercator.x = x;
mercator.y = y;
return mercator;
}
//墨卡托转经纬度
WayPoint Mercator2lonLat(WayPoint mercator)
{
WayPoint lonLat;
double x = mercator.x / 20037508.34 * 180;
double y = mercator.y / 20037508.34 * 180;
y = 180 / Pi * (2 * atan(exp(y * Pi / 180)) - Pi / 2);
lonLat.x = x;
lonLat.y = y;
return lonLat;
}