排版方式:
行级元素(inline):使用$...$,表示公式的首尾
块级元素(displayed):使用$$...$$,默认居中显示
LaTex数学符号表
小写希腊字母

大写希腊字母

数学函数名

二元关系符

二元运算符

大尺寸运算符
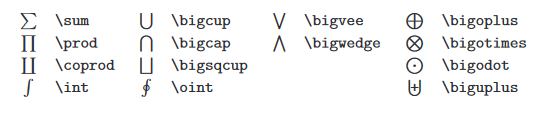
箭头

定界符

大尺寸定界符
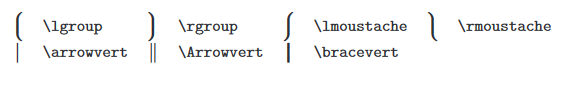
其它符号

AMS二元关系符

AMS二元否定关系符和箭头
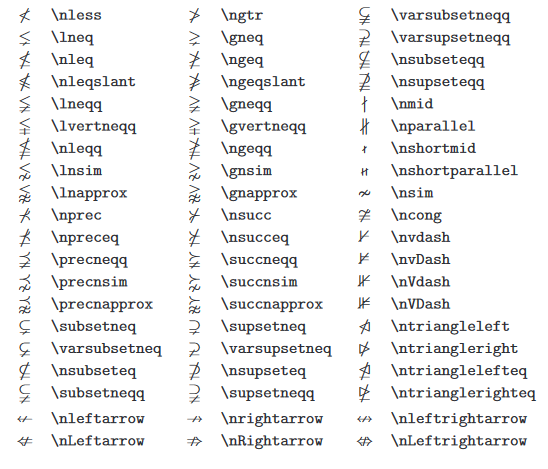
举例:
$$
x_i^2
$$
[x_i^2
]
$$
log_2 x
$$
[log_2 x
]
$$
10^{10}
$$
[10^{10}
]
$$
{1+2}
$$
[ {1+2}
]
$$
frac{1+1}{2}+1
$$
[frac{1+1}{2}+1
]
$$
sum_1^n
$$
[sum_1^n
]
$$
int_1^n
$$
[int_1^n
]
$$
lim_{x oinfty}
$$
[lim_{x oinfty}
]
$$
egin{matrix}
1 & x & x^2 \
1 & y & y^2 \
1 & z & z^2 \
end{matrix}
$$
[egin{matrix}
1 & x & x^2 \
1 & y & y^2 \
1 & z & z^2 \
end{matrix}
]
$$
h( heta) = sum_{j=0}^n heta_jx_j
$$
[h( heta) = sum_{j=0}^n heta_jx_j
]
$$
frac{partial J( heta)}{partial heta_j} = -frac{1}{m}sum_{i=0}^m(y^i-h_ heta(x^i))x_j^i
$$
[frac{partial J( heta)}{partial heta_j} = -frac{1}{m}sum_{i=0}^m(y^i-h_ heta(x^i))x_j^i
]
$$
f(n) =
egin{cases}
n/2, & ext{if $n$ is even} \
3n+1, & ext{if $n$ is odd}
end{cases}
$$
[f(n) =
egin{cases}
n/2, & ext{if $n$ is even} \
3n+1, & ext{if $n$ is odd}
end{cases}
]
$$
left{
egin{array}{}
a_1x+b_1y+c_1z = d_1\
a_2x+b_2y+c_2z = d_2\
a_3x+b_3y+c_3z = d_3
end{array}
ight.
$$
[left{
egin{array}{}
a_1x+b_1y+c_1z = d_1\
a_2x+b_2y+c_2z = d_2\
a_3x+b_3y+c_3z = d_3
end{array}
ight.
]
$$
X = left(
egin{matrix}
x_{11} &x_{12}&cdots&x_{1d}\
x_{21} &x_{22}&cdots&x_{2d}\
vdots&vdots&ddots&vdots\
x_{m1}&x_{m2}&cdots&x_{md}
end{matrix}
ight)
= left(
egin{matrix}
x_1^T\
x_2^T\
vdots\
x_m^T\
end{matrix}
ight)
$$
[X = left(
egin{matrix}
x_{11} &x_{12}&cdots&x_{1d}\
x_{21} &x_{22}&cdots&x_{2d}\
vdots&vdots&ddots&vdots\
x_{m1}&x_{m2}&cdots&x_{md}
end{matrix}
ight)
= left(
egin{matrix}
x_1^T\
x_2^T\
vdots\
x_m^T\
end{matrix}
ight)
]
$$
egin{align}
frac{partial J( heta)}{partial heta_j}
& = -frac{1}{m}sum_{i=0}^m(y^i-h_ heta(x^i))frac{partial}{partial heta_j}(y^i-h_ heta(x^i)) \
& = -frac{1}{m}sum_{i=0}^m(y^i-h_ heta(x^i))frac{partial}{partial heta_j}(sum_{j=0}^n heta_jx_j^i-y^i) \
& = -frac1msum_{i=0}^m(y^i-h_ heta(x^i))x_i^j
end{align}
$$
[egin{align}
frac{partial J( heta)}{partial heta_j}
& = -frac{1}{m}sum_{i=0}^m(y^i-h_ heta(x^i))frac{partial}{partial heta_j}(y^i-h_ heta(x^i)) \
& = -frac{1}{m}sum_{i=0}^m(y^i-h_ heta(x^i))frac{partial}{partial heta_j}(sum_{j=0}^n heta_jx_j^i-y^i) \
& = -frac1msum_{i=0}^m(y^i-h_ heta(x^i))x_i^j
end{align}
]
$$
sqrt{x^2+sqrt{y}} \
sqrt[3]{2} \
$$
[sqrt{x^2+sqrt{y}} \
sqrt[3]{2} \
]
$$
overline{m+n} qquad
underline{m+n}
$$
[overline{m+n} qquad
underline{m+n}
]
$$
underbrace{a+b+cdots+z}_{26}
$$
[underbrace{a+b+cdots+z}_{26}
]
$$
vec{a} quad
overrightarrow{AB}
$$
[vec{a} quad
overrightarrow{AB}
]
$$
v = sigma_1 cdot sigma_2 au_1 cdot au_2
$$
[v = sigma_1 cdot sigma_2 au_1 cdot au_2
]
$$
lim_{x
ightarrow 0} frac{sin x}{x}=1
$$
[lim_{x
ightarrow 0} frac{sin x}{x}=1
]
$$
mathop{min_{G} max_{D}}
$$
[mathop{min_{G} max_{D}}
]
Reference: