1584. 连接所有点的最小费用-图/最小生成树-中等

问题描述

给你一个points 数组，表示 2D 平面上的一些点，其中 points[i] = [xi, yi] 。

连接点 [xi, yi] 和点 [xj, yj] 的费用为它们之间的 曼哈顿距离 ：|xi - xj| + |yi - yj| ，其中 |val| 表示 val 的绝对值。

请你返回将所有点连接的最小总费用。只有任意两点之间 有且仅有 一条简单路径时，才认为所有点都已连接。

输入：points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
输出：20
解释：

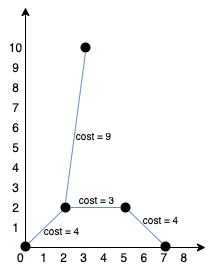
我们可以按照上图所示连接所有点得到最小总费用，总费用为 20 。
注意到任意两个点之间只有唯一一条路径互相到达。

示例 2：

输入：points = [[3,12],[-2,5],[-4,1]]
输出：18
示例 3：

输入：points = [[0,0],[1,1],[1,0],[-1,1]]
输出：4
示例 4：

输入：points = [[-1000000,-1000000],[1000000,1000000]]
输出：4000000
示例 5：

输入：points = [[0,0]]
输出：0
 

提示：

1 <= points.length <= 1000
-106 <= xi, yi <= 106
所有点 (xi, yi) 两两不同。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/min-cost-to-connect-all-points

解答

/*prim算法，算法描述,请参考别人写的文章https://blog.csdn.net/qq_37241934/article/details/81133651
本题就是用prim算法构建一颗最小生成树。

*/
class Solution {
    int n;
    public int minCostConnectPoints(int[][] points) {
        n = points.length;
        int[][] costs = new int[n][n];//记录costs[i][j]表示i到j的距离（开销）。
        for(int i=0;i<n;i++){
            for(int j=0;j<n;j++){
                costs[i][j] = Math.abs(points[i][0]-points[j][0])+Math.abs(points[i][1]-points[j][1]);
            }
        }
        return minimumSpanningTree(costs, 0);//以0为起点，建立最小生成树。
    }
    public int minimumSpanningTree(int[][] costs, int start){
        int res = 0;
        int treeNode = 1;//节点数量, 初始树节点数量为1
        int[] lowCosts = new int[n];//lowCosts[i]表示：节点i到生成树中的某个节点(比如最开始是到start)的最小权值（开销）。
        int[] mts = new int[n];//mts[i]表示：距离节点i最近的一个生成树中的节点。
        //下面要初始化这两个数组
        for(int i=0;i<n;i++){
            lowCosts[i] = costs[start][i];
            mts[i] = i==start?-1:start;//mts[i]=-1表示i节点已经是生成树中的一员了。
        }
        
        while(treeNode<n){
            int newNode = -1;
            int min = Integer.MAX_VALUE;
            //下面寻找新的节点,将lowCosts中的最小值选出来作为新节点。
            for(int i=0;i<n;i++){
                if(mts[i]!=-1 && lowCosts[i]<min){
                    newNode = i;
                    min = lowCosts[i];
                }
            }
            //newNode!=-1表示找到了新的可以加入树的节点，那么找到了之后就要用newNode作为start，所以要更新两个数组。
            if(newNode!=-1){
                treeNode++;
                mts[newNode]=-1;//把newNode加入生成树
                res+=min;//更新距离
                //下面更新数组。
                for(int i=0;i<n;i++){
                    if(mts[i]!=-1 && costs[newNode][i]<lowCosts[i]){
                        lowCosts[i] = costs[newNode][i];
                        mts[i] = newNode;
                    }
                }
            }
        }
        return res;
    }
}