1514. 概率最大的路径-动态规划、图-中等难度

问题描述

给你一个由 n 个节点（下标从 0 开始）组成的无向加权图，该图由一个描述边的列表组成，其中 edges[i] = [a, b] 表示连接节点 a 和 b 的一条无向边，且该边遍历成功的概率为 succProb[i] 。

指定两个节点分别作为起点 start 和终点 end ，请你找出从起点到终点成功概率最大的路径，并返回其成功概率。

如果不存在从 start 到 end 的路径，请 返回 0 。只要答案与标准答案的误差不超过 1e-5 ，就会被视作正确答案。

示例 1：

 

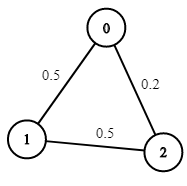
输入：n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2
输出：0.25000
解释：从起点到终点有两条路径，其中一条的成功概率为 0.2 ，而另一条为 0.5 * 0.5 = 0.25
示例 2：

 

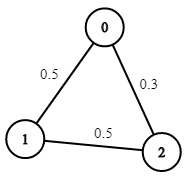
输入：n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], start = 0, end = 2
输出：0.30000
示例 3：

 

输入：n = 3, edges = [[0,1]], succProb = [0.5], start = 0, end = 2
输出：0.00000
解释：节点 0 和 节点 2 之间不存在路径
 

提示：

2 <= n <= 10^4
0 <= start, end < n
start != end
0 <= a, b < n
a != b
0 <= succProb.length == edges.length <= 2*10^4
0 <= succProb[i] <= 1
每两个节点之间最多有一条边

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/path-with-maximum-probability

解答

//动态规划。dp[i]表示到达节点i的最大概率。
class Solution {
    public double maxProbability(int n, int[][] edges, double[] succProb, int start, int end) {
        double[] dp = new double[n];
        dp[start] = 1;
        while(true){
            boolean k = false;
            for(int i=0;i<edges.length;i++){
                if(dp[edges[i][0]]*succProb[i] > dp[edges[i][1]]){
                    dp[edges[i][1]] = dp[edges[i][0]]*succProb[i];
                    k = true;
                }
                if(dp[edges[i][1]]*succProb[i] > dp[edges[i][0]]){
                    dp[edges[i][0]] = dp[edges[i][1]]*succProb[i];
                    k = true;
                }
            }
            if(!k)break;
        }
        return dp[end];
    }
}

/*超时的dfs
class Solution {
    Map<Integer,List<Integer>> map;
    Map<Integer,Integer> count;
    public void dfs(List<List<Integer>> res, int s, int e, List<Integer> temp){
        if(count.get(s)!=1)return;
        temp.add(s);
        count.put(s, 0);
        if(s == e)res.add(new ArrayList<Integer>(temp));
        else for(int i:map.get(s))dfs(res, i, e, temp);
        count.put(s, 1);
        temp.remove(new Integer(s));
    }
    public double maxProbability(int n, int[][] edges, double[] succProb, int start, int end) {
        List<List<Integer>> edge = new ArrayList<List<Integer>>();
        for(int[] temp:edges){
            List<Integer> t = new ArrayList<Integer>();
            for(int k:temp){
                t.add(k);
            }
            edge.add(new ArrayList<Integer>(t));
        }
        int i;
        count = new HashMap<Integer,Integer>();
        map = new HashMap<Integer,List<Integer>>();
        for(i=0;i<n;i++){
            count.put(i,1);
            map.put(i,new ArrayList<Integer>());
        }
        for(int[] temp:edges){
            map.get(temp[0]).add(temp[1]);
            map.get(temp[1]).add(temp[0]);
        }
        //先列出所有的可能路径，保存在res中。
        List<List<Integer>> res = new ArrayList<List<Integer>>();
        dfs(res, start, end, new ArrayList<Integer>());
        //System.out.println(res);
        if(res.size() == 0)return 0;
        else{
            double p, max = -1;
            int k, index;
            for(List<Integer> t:res){
                p = 1;
                for(k=0;k<t.size()-1;k++){
                    index = 0;
                    for(List<Integer> l:edge){
                        if(l.contains(t.get(k)) && l.contains(t.get(k+1)))break;
                        index++;
                    }
                    p *= succProb[index];
                }
                if(p > max)max = p;
            }
            return max;
        }
    }
}
*/