树这个数据结构内容真的很多,上一节所讲的二叉堆,其实就是一颗二叉树,这次讲的左偏树(又叫“左翼堆”),也是树。
二叉堆是个很不错的数据结构,因为它非常便于理解,而且仅仅用了一个数组,不会造成额外空间的浪费,但它有个缺点,那就是很难合并两个二叉堆,对于 “合并”,“拆分”这种操作,我觉得最方面的还是依靠指针,改变一下指针的值就可以实现,要是涉及到元素的移动,那就复杂一些了。
左偏树跟二叉堆比起来,就是一棵真正意义上的树了,具有左右指针,所以空间开销上稍微大一点,但却带来了便于合并的便利。BTW:写了很多很多的程序之后,我发觉“空间换时间”始终是个应该考虑的编程方法。:)
左偏左偏,给人感觉就是左子树的比重比较大了,事实上也差不多,可以这么理解:左边分量重,那一直往右,就一定能最快地找到可以插入元素的节点了。 所以可以这样下个定义:左偏树就是对其任意子树而言,往右到插入点的距离(下面简称为“距离”)始终小于等于往左到插入点的距离,当然了,和二叉堆一样, 父节点的值要小于左右子节点的值。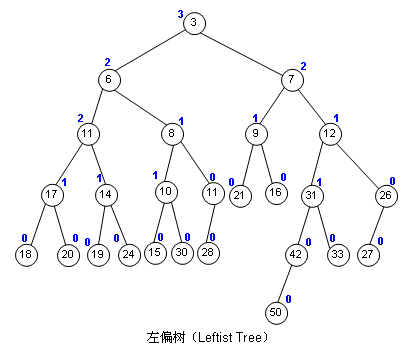
如果节点本身不满,可插入,那距离就为0,再把空节点的距离记为-1,这样我们就得出:父节点的距离 = 右子节点距离 + 1,因为右子节点的距离始终是小于等于左子节点距离的。我把距离的值用蓝色字体标在上图中了。
左偏树并一定平衡,甚至它可以很不平衡,因为它其实也不需要平衡,它只需要像二叉堆那样的功能,再加上合并方便,现在来看左偏树的合并算法,如图: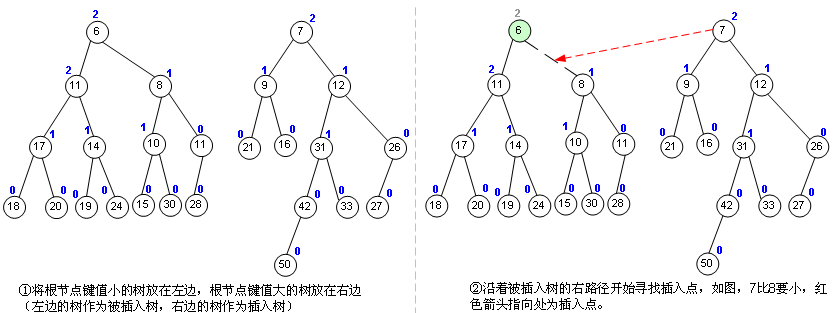
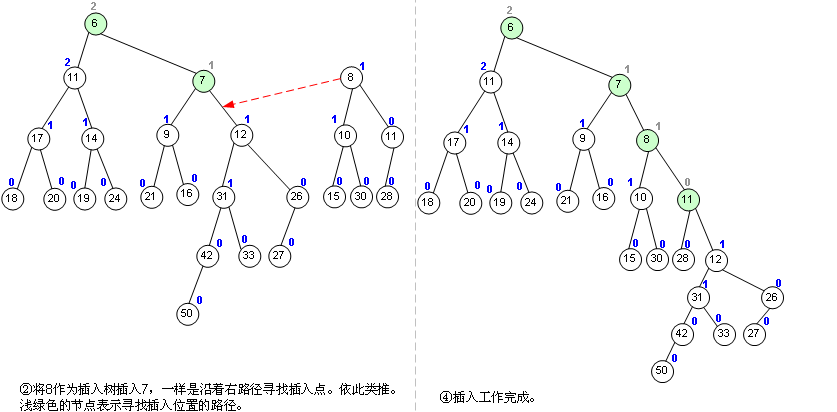
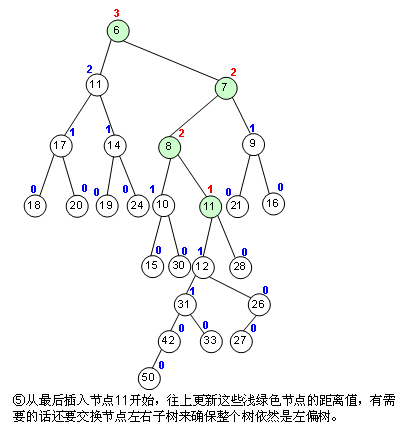
这种算法其实很适合用递归来做,但我还是用了一个循环,其实也差不多。对于左偏树来说,这个合并操作是最重要最基本的了。为什么?你看 哦:Enqueue,我能不能看作是这个左偏树的root和一个单节点树的合并?而Dequeue,我能不能看作是把root节点取出来,然后合并 root的左右子树?事实上就是这样的,我提供的代码就是这样干的。
Conclusion:左偏树比同二叉堆的优点就是方便合并,缺点是编程复杂度略高(也高不去哪),占用空间稍大(其实也大不去哪)。附上代码,老样子了,单个文件,直接调试的代码,零依赖零配置,一看就懂,代码虽然不算完美,但作为演示和学习,是足够了。
原文(http://www.cppblog.com/guogangj/archive/2009/10/30/99833.html)