2017 ICPC 北京站 E F J G H

Cats and Fish

• 题意: n只猫,m条鱼,第i只猫吃一只鱼需要(C_i),每只猫吃完当前这条鱼立即去吃下一条,问(T)时刻还剩多少条鱼,有多少条鱼正在被吃
• 思路: 以为是贪心,但是wa了(不懂),要模拟,具体看注释吧

const int N = 2*1e5+10;

int n,m,k;
int a[N];
int v[N];

int main(){
	while(scanf("%d%d%d",&m,&n,&k)==3){
		int q = 0, p = 0 , t = m;	// q 被猫拿走的鱼, p 被猫吃完的鱼, t 还剩多少条鱼
		for(int i=1;i<=n;++i)	scanf("%d",&a[i]);
		sort(a+1,a+1+n);	// 吃的快的猫先拿
		for(int i=1;i<=k;++i){	// 时间
			for(int j=1;j<=n;++j){
				if(t==0)	break;
				if(i%a[j]==1 || a[j]==1){	// 余数是1或吃鱼时间为1,当前这只猫拿鱼
					t--;
					q++;
				}
				if(i%a[j]==0){	// 整除,说明这只猫吃掉一条鱼
					p++;
				}
			}
		}
		printf("%d %d
",m-q,q-p);// m-q 没有被猫拿走的鱼, p-q 被拿走但没有被吃完的鱼
	}

	return 0;
}

Secret Poems

• 题意: 给出一个字母矩阵,原来按照对角线s型排列,让你转换成回型排列
• 思路: bfs,遇到边界拐弯.

const int N = 120;

char s[N*N];
char a[N][N],b[N][N];
int vis[N][N];
int n;
void dfs(int x,int y,int dep){
// cout << x << ' ' << y << endl;
	if(dep>n*n)	return;
	s[dep] = a[x][y];
	vis[x][y] = 1;
	if(x==1){
		if(y-1>0 && !vis[x+1][y-1]){
			dfs(x+1,y-1,dep+1);
		}else if(y+1<=n && !vis[x][y+1]){
			dfs(x,y+1,dep+1);
		}else{
			dfs(x+1,y,dep+1);
		}
	}else if(x==n){
		if(y+1<=n && !vis[x-1][y+1]){
			dfs(x-1,y+1,dep+1);
		}else{
			dfs(x,y+1,dep+1);
		}
	}else if(y==1){
		if(x-1>0 && !vis[x-1][y+1]){
			dfs(x-1,y+1,dep+1);
		}else{
			dfs(x+1,y,dep+1);
		}
	}else if(y==n){
		if(x+1<=n && !vis[x+1][y-1]){
			dfs(x+1,y-1,dep+1);
		}else{
			dfs(x+1,y,dep+1);
		}
	}else{
		if(x-1>0 && y+1<=n && !vis[x-1][y+1]){
			dfs(x-1,y+1,dep+1);
		}else if(x+1<=n && y-1>0 && !vis[x+1][y-1]){
			dfs(x+1,y-1,dep+1);
		}
	}
}
int d[][2] ={{0,1},{1,0},{0,-1},{-1,0}};
void dfs2(int x,int y,int dep,int dir){
	b[x][y] = s[dep];
	vis[x][y] = 1;
	int tx = d[dir][0]+x, ty = d[dir][1]+y;
	if(tx<=n && tx>0 && ty<=n && ty>0 && !vis[tx][ty])	dfs2(tx,ty,dep+1,dir);
	else{
		dir = (dir+1)%4;
		tx = d[dir][0]+x, ty = d[dir][1]+y;
		if(tx<=n && tx>0 && ty<=n && ty>0 && !vis[tx][ty])	dfs2(tx,ty,dep+1,dir);
	}
}
int main(){
	while(scanf("%d",&n)==1){
		memset(vis,0,sizeof vis);
		for(int i=1;i<=n;++i){
			scanf("%s",a[i]+1);
		}
		dfs(1,1,1);
		memset(vis,0,sizeof vis);
		dfs2(1,1,1,0);
		for(int i=1;i<=n;++i){
			for(int j=1;j<=n;++j){
				putchar(b[i][j]);
			}putchar('
');
		}
	}

	return 0;
}

Pangu and Stones

• 题意: 合并石子,每次可以合并长度(lsim r)的区间,问合并成一堆的最小值
• 思路: 优先队列模拟直接WA掉, dp[i][j][k] 表示从i到j合并成k堆的最小值

dp[l][r][p] = min dp[l][k][p-1] + dp[k+1][j][1] (i<=k<j,2<=p<=r)
dp[l][r][1] = min dp[l][r][p] + sum[l] - sum[r] (l<=p<=r)

先考虑合并成一堆,只能通过合并(lsim r)个堆.
合并成多堆时,选择后面一个堆,合并到前面p-1个堆,实质是转移p堆的值没有实际进行合并

int a[N],sum[N];
int dp[N][N][N];
int n,l,r;
int main(){
	while(scanf("%d%d%d",&n,&l,&r)==3){
		memset(dp,0x3f,sizeof dp);
		for(int i=1;i<=n;++i){
			scanf("%d",&a[i]);
			sum[i] = sum[i-1]+a[i];
		}
		for(int i=1;i<=n;++i){
			for(int j=i;j<=n;++j){
				dp[i][j][j-i+1] = 0;
			}
		}
		for(int len = 2;len<=n;++len){
			for(int i=1;i+len-1<=n;++i){
				int j = i+len-1;
				for(int p=2;p<=r;++p){
					for(int k=i;k<j;++k){
						if(k-i+1<p-1)	continue;	// k到i 不够p-1个数 肯定合不成p-1个堆
						dp[i][j][p] = min(dp[i][j][p],dp[i][k][p-1]+dp[k+1][j][1]);
					}
				}
				for(int p=l;p<=r;++p){
					dp[i][j][1] = min(dp[i][j][1],dp[i][j][p]+sum[j]-sum[i-1]);
				}
			}
		}
		if(dp[1][n][1]==0x3f3f3f3f)	dp[1][n][1] = 0;	// 没有更新到最终的区间 无解
		printf("%d
",dp[1][n][1]);
	}
	return 0;
}

Liaoning Ship’s Voyage

• 题意: 八连通,经典bfs,但加入了一个不可经过的三角形区域,问从左下角到右上角的最短路
• 思路: 一开始写预处理所有三角形内部的点,设置其不可经过,但这题值域并不是整数范围,需要在bfs到下一个点时判断路径是否经过了三角形(离散枚举100个点)

const int N = 40;
const double eps = 1e-7;
const int dir[][2] = {{0,1},{1,0},{0,-1},{-1,0},{-1,-1},{1,1},{1,-1},{-1,1}};

struct point {
    double x,y;
    point(double x=0.0,double y=0.0):x(x),y(y){}
    double det(const point oth)const{
        return x*oth.y - y*oth.x;
    }
    point operator - (const point oth)const{
        return point(x-oth.x,y-oth.y);
    }
}p[3];
struct node{
    int x,y,dep;
    node(int x=0,int y=0,int dep=0):x(x),y(y),dep(dep){}
}cur,nxt;


char ma[N][N];
int vis[N][N];
int n;

int dcmp(double x){
    if(fabs(x)<eps) return 0;
    if(x>0) return 1;
    return -1;
}
double cross(point a,point b){return a.x*b.y - a.y*b.x;}
bool check(point pt){	
    // point p1 = p[0]- pt, p2 = p[1] - pt , p3 = p[2]-pt;
    point p1 = pt - p[0],   p2 = pt - p[1], p3 = pt - p[2];
    int r1 = dcmp(cross(p1,p2)), r2 = dcmp(cross(p2,p3)), r3 = dcmp(cross(p3,p1));
    return r1+r2+r3==3||r1+r2+r3==-3;
}
void bfs(){
    queue<node> que;
    que.push(node(0,0,0));
    vis[0][0] = 1;
    double tmpx,tmpy,dx,dy; 
    int sign;
    while(!que.empty()){
        cur = que.front();  que.pop();
        if(cur.x == n-1 && cur.y == n-1){
            printf("%d
",cur.dep);
            return ;
        }
        nxt.dep = cur.dep+1;
        for(int i=0;i<8;++i){
            nxt.x = cur.x + dir[i][0];
            nxt.y = cur.y + dir[i][1];
            if(nxt.x >=0 && nxt.x <n && nxt.y>=0 && nxt.y <n && !vis[nxt.x][nxt.y] && ma[nxt.x][nxt.y]=='.'){
                tmpx =cur.x;    tmpy = cur.y;   // 经过点
                dx = 1.0*dir[i][0]/100; dy = 1.0*dir[i][1]/100;	// 步长
                sign = 0;
                for(int j=0;j<=100;++j){
                    if(check(point(tmpy,tmpx))){// 题目的x(行),y(列)和存储的x(列),y(行)是相反的
                        sign  = 1;break;
                    }
                    tmpx += dx; tmpy += dy;
                }
                if(sign==0){	// 没经过三角形,才可以走这个方向
                    vis[nxt.x][nxt.y] = 1;
                    que.push(nxt);
                }
            }
        }
    }
    printf("-1
");
    return ;
}
int main(){
    while(scanf("%d",&n)==1){
        memset(vis,0,sizeof vis);
        for(int i=0;i<3;++i){
            scanf("%lf%lf",&p[i].x,&p[i].y);
        }
        for(int i=n-1;i>=0;--i){
            scanf("%s",ma[i]);
        }
        bfs();
    }
    return 0;
}

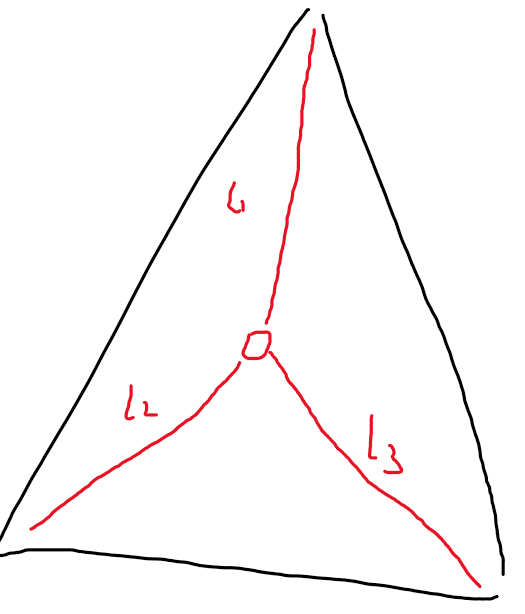
l1,l2,l3顺序排列,点在凸多边形内必定有相同的转向(l2在l1左,l3在l2左,l1在l3左)可以O(n)判断在凸多边形内O(logn)太麻烦

Puzzle Game

• 题意: 可以修改矩阵中一个值为K,求最大子矩阵和最小
• 思路: 如果要修改肯定在最大子矩阵内部,枚举最大子矩阵元素进行修改,修改后的最大子矩阵等于 max(上方最大子矩阵和，下方最大子矩阵和，左方最大子矩阵和，右方最大子矩阵和，包含这个点后的最大子矩阵和 利用当前最大的和维护 )

#include<bits/stdc++.h>

using namespace std;
const int INF = 0x3f3f3f3f;
const int N = 510;
int n,m,p;
int sum[N],dp[N],u[N],d[N],r[N],l[N];
int a[N][N];

void solve1(){
    memset(dp,0,sizeof dp);
    for(int i=1;i<=n;++i){
        memset(sum,0,sizeof sum);
        for(int j=i;j<=n;++j){
            int t = -1*INF, tmp = t;
            for(int k=1;k<=m;++k){
                sum[k] += a[j][k];
                dp[k] = max(dp[k-1],0)+sum[k];
                tmp = max(dp[k],tmp);
            }
            for(int k=j;k<=n;++k)   u[k] = max(u[k],tmp);	// 上
            for(int k=1;k<=i;++k)   d[k] = max(d[k],tmp);	// 下
        }
    }    
    memset(dp,0,sizeof dp);
    for(int i=1;i<=m;++i){
        memset(sum,0,sizeof sum);
        for(int j=i;j<=m;++j){
            int t = -1*INF, tmp = t;
            for(int k=1;k<=n;++k){
                sum[k] += a[k][j];
                dp[k] = max(dp[k-1],0)+sum[k];
                tmp = max(dp[k],tmp);
            }
            for(int k=j;k<=m;++k)   l[k] = max(l[k],tmp);	// 左
            for(int k=1;k<=i;++k)   r[k] = max(r[k],tmp);	// 右
        }
    }
}

int main(){
    while(scanf("%d%d%d",&n,&m,&p)==3){
        fill(l,l+400,-1*INF);
        fill(d,d+400,-1*INF);
        fill(u,u+400,-1*INF);
        fill(r,r+400,-1*INF);
        for(int i=1;i<=n;++i){
            for(int j=1;j<=m;++j)   scanf("%d",&a[i][j]);
        }
        solve1();
        int ans1=  u[n];
        for(int i=1;i<=n;++i){
            for(int j=1;j<=m;++j){
                if(a[i][j]<=p)  continue;
                int ans = -1*INF;
                ans = max(u[i-1],d[i+1]);
                ans = max(ans,max(l[j-1],r[j+1]));
                ans1 = min(ans1,max(u[n]-a[i][j]+p,ans));	// 要计算整个矩阵修改后的和
            }
        }
        printf("%d
",ans1);
    }
}

博客连接
Puzzle Game