核(kernels)
将特征x映射到另一组特征上，比如将x映射到x,x^2,x^3上，并将这个映射组成的向量记为phi。
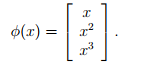将学习算法中的x换成phi(x)。
定义核函数
。使用核函数代替phi(x)的内积。
假设有两个变量特征，假设核函数等于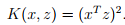
将式子变形可以得到
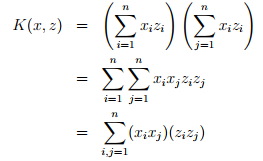
所以对应的phi(x)等于
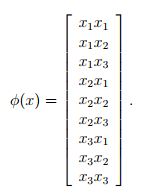
为了计算出phi(x)需要时间复杂度为O(n^2)，n代表x的维度。但是去计算核函数的值只需要O(n)的时间复杂度。
核函数的推广
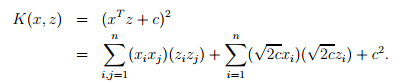
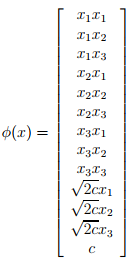
对于任意给出的一些东西，要对其分类，如果希望学习算法认为x和z是相近的，那么需要尝试找到一个核K(x,z)取一个较大的值，反之，取一个较小的值。所以，根据这种思想，可以写出高斯核函数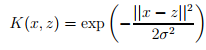
。
判断核函数是否有效
对于给定的核函数，判断其是否为有效核函数，即为是否能找到一个映射phi，使得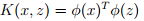
成立。
假设K是一个有效核函数，对于任意给定点集合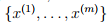
，定义核矩阵k(m*m)。矩阵上的值与核函数相对应，即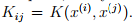
对于任意给定的m维向量z，考虑
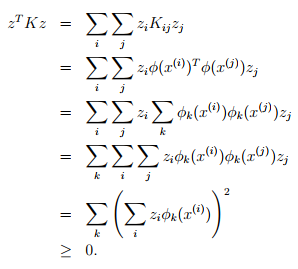这说明了k是半正定矩阵，即k>0。
所以，如果一个核函数是有效的，那么核矩阵应该是对称半正定矩阵。
L1 norm soft margin SVM
让算法能够处理非线性可分数据集以及忽略一些异常值，对之前的算法进行修改，加上惩罚项，
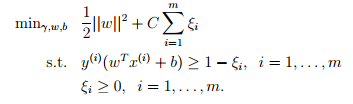
对应的lagrange算子为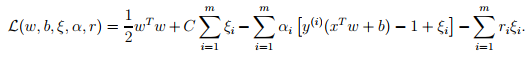
。这个优化问题的对偶问题为
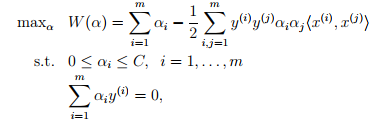
对应的KKT条件为
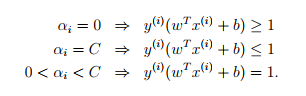
坐标上升算法(coordinate ascent)
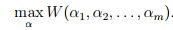，使W函数最大化，坐标上升算法的过程为，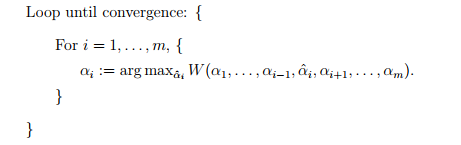
坐标上升算法与其他算法相比，迭代次数会较多，但是代价会较少。但是坐标上升的基本形式不能直接用于SVM对偶优化问题的求解上面。
序列最小优化算法（SMO）
坐标上升算法改变一个alpha的值，SMO一次改变两个alpha的值。想解决的对偶优化问题如下，
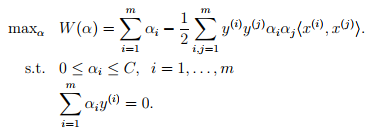
算法思路为，循环直至收敛{
1.根据启发式规则选取要改变的alpha_i,alpha_j。
2.保持除这两个参数之外的其他参数值不变，同时相对于这两个参数使得W取最优。
}
假设固定a1,a2以外的其他参数不变，则约束可以写成，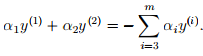
画出下图，
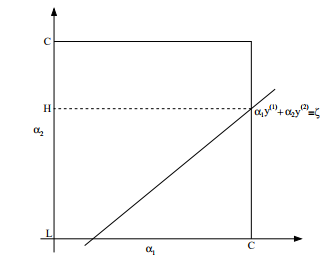
可以将w转化为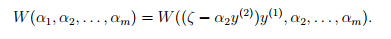
由w的定义可以得到，w对每一个参数来说都是二次函数。所以固定其他参数不变的情况下，对alpha2来说，就是一个二次函数，
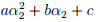。结合上图中的方形约束，直线以及该二次函数，便可以求出alpha2,然后带入等式得出alpha1，这样就可以求得相对于alpha1,alpha2的w最优值。