十九、最小生成树（普里姆算法）

普里姆算法介绍

普里姆(Prim)算法，是用来求加权连通图的最小生成树的算法。

基本思想 
对于图G而言，V是所有顶点的集合；现在，设置两个新的集合U和T，其中U用于存放G的最小生成树中的顶点，T存放G的最小生成树中的边。 从所有uЄU，vЄ(V-U) (V-U表示出去U的所有顶点)的边中选取权值最小的边(u, v)，将顶点v加入集合U中，将边(u, v)加入集合T中，如此不断重复，直到U=V为止，最小生成树构造完毕，这时集合T中包含了最小生成树中的所有边。

普里姆算法图解

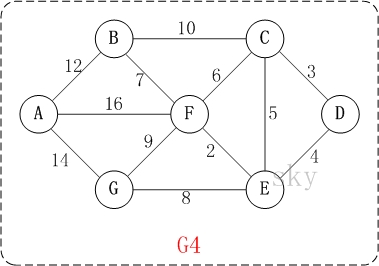
以上图G4为例，来对普里姆进行演示(从第一个顶点A开始通过普里姆算法生成最小生成树)。

初始状态：V是所有顶点的集合，即V={A,B,C,D,E,F,G}；U和T都是空！ 
第1步：将顶点A加入到U中。 
    此时，U={A}。 
第2步：将顶点B加入到U中。 
    上一步操作之后，U={A}, V-U={B,C,D,E,F,G}；因此，边(A,B)的权值最小。将顶点B添加到U中；此时，U={A,B}。 
第3步：将顶点F加入到U中。 
    上一步操作之后，U={A,B}, V-U={C,D,E,F,G}；因此，边(B,F)的权值最小。将顶点F添加到U中；此时，U={A,B,F}。 
第4步：将顶点E加入到U中。 
    上一步操作之后，U={A,B,F}, V-U={C,D,E,G}；因此，边(F,E)的权值最小。将顶点E添加到U中；此时，U={A,B,F,E}。 
第5步：将顶点D加入到U中。 
    上一步操作之后，U={A,B,F,E}, V-U={C,D,G}；因此，边(E,D)的权值最小。将顶点D添加到U中；此时，U={A,B,F,E,D}。 
第6步：将顶点C加入到U中。 
    上一步操作之后，U={A,B,F,E,D}, V-U={C,G}；因此，边(D,C)的权值最小。将顶点C添加到U中；此时，U={A,B,F,E,D,C}。 
第7步：将顶点G加入到U中。 
    上一步操作之后，U={A,B,F,E,D,C}, V-U={G}；因此，边(F,G)的权值最小。将顶点G添加到U中；此时，U=V。

此时，最小生成树构造完成！它包括的顶点依次是：A B F E D C G。

邻接矩阵：

class Vertex
{
    public char label;
    public boolean wasVisited;
    public Vertex(char lab)
    {
        label = lab;
        wasVisited = false;
    }
}

class UDGraph
{
    private final int MAX_VERTS = 20;
    private Vertex vertexList[];
    private int adjMat[][];
    private int nVerts;
    
    public UDGraph()
    {
        vertexList = new Vertex[MAX_VERTS];
        adjMat = new int[MAX_VERTS][MAX_VERTS];
        nVerts = 0;
        for(int i=0;i<MAX_VERTS;i++)
            for(int j=0;j<MAX_VERTS;j++)
                //最大值表示刚开始顶点间都不连接
                adjMat[i][j] = Integer.MAX_VALUE;
    }
    
    public void addVertex(char lab)
    {
        vertexList[nVerts++] = new Vertex(lab);
    }
    
    public void addEdge(int start,int end,int weight)
    {
        adjMat[start][end] = weight;
        adjMat[end][start] = weight;//无向图
    }
    
    //最开始以vertexList[v]为最小生成树的起点
    public void Prim(int v)
    {
        //存放剩余顶点到当前生成树的最短的一条边的权值
        int lowcost[] = new int[MAX_VERTS];
        int k=0;
        for(int i=0;i<nVerts;i++)
        {
            //将vertexList数组下标第v个顶点到其它顶点的所有边当作候选边
            lowcost[i] = adjMat[v][i];
        }
        //将vertexList[v]并入树中
        vertexList[v].wasVisited = true;
        System.out.println(vertexList[v].label);
        //选中某个顶点后（这里是v）,每次选取剩下顶点中的一个，一共要有nVerts-1个次
        for(int i=0;i<nVerts-1;i++)
        {
            int min = Integer.MAX_VALUE;
            //选出剩下顶点到生成数的最小边
            for(int j=0;j<nVerts;j++)
            {
                if(!vertexList[j].wasVisited && lowcost[j]<min)
                {
                    min = lowcost[j];
                    k=j;
                }
            }
            vertexList[k].wasVisited = true;
            System.out.println("----"+lowcost[k]+"----"+vertexList[k].label);
            //将顶点k并入生成树，并更新剩下顶点到该生成树的最小边
            for(int m=0;m<nVerts;m++)
            {
                //如果剩余顶点到k并入后的生成树的最小边小于并入前的生成树的最小边
                if(!vertexList[m].wasVisited && adjMat[k][m]<lowcost[m])
                    lowcost[m] = adjMat[k][m];
            }
         }
     }
 }
public class MatrixUDG_Prim 
{
    public static void main(String[] args) 
    {
          UDGraph theGraph = new UDGraph();
          theGraph.addVertex('A');// 0 
          theGraph.addVertex('B');// 1
          theGraph.addVertex('C');// 2
          theGraph.addVertex('D');// 3
          theGraph.addVertex('E');// 4
          theGraph.addVertex('F');// 5

          theGraph.addEdge(0, 1,1);//AB
          theGraph.addEdge(0, 2,4);//AC
          theGraph.addEdge(0, 5,6);//AF
          theGraph.addEdge(1, 3,8);//BD
          theGraph.addEdge(1, 4,3);//BE
          theGraph.addEdge(2, 4,9);//CE
          theGraph.addEdge(2, 5,5);//CF
          theGraph.addEdge(3, 4,7);//DE
          theGraph.addEdge(3, 5,10);//DF
          theGraph.addEdge(4, 5,2);//EF//从0开始，即顶点A开始
          theGraph.Prim(0);
    }
}

邻接表：

import java.util.ArrayList;
class Vertex
{
    public char label;
    public boolean wasVisited;
    public Edge firstEdge;
    
    public Vertex(char lab)
    {
        this.label = lab;
        this.wasVisited = false;
        firstEdge = null;
    }
}

class Edge
{
    public int dest;
    public int weight;
    public Edge nextEdge;
    public Edge(int dest,int weight)
    {
        this.dest= dest;
        this.weight = weight;
        nextEdge = null;
    }
}

class UDGraph
{
    private final int MAX_VERTS = 20;//图的最大顶点数
    private int nVerts = 0;//当前顶点数
    private Vertex vertexList[];//顶点链表
    
    public UDGraph()
    {
        vertexList = new Vertex[MAX_VERTS];    
    }
    
    public void addVertex(char lab)
    {
        vertexList[nVerts++] = new Vertex(lab);
    }
    
    public void addEdge(int start,int end,int weight)
    {
        Edge startEdge = new Edge(start,weight);
        Edge endEdge = new Edge(end,weight);
        Edge edge2 = vertexList[start].firstEdge;
        if(edge2==null)
        {
            vertexList[start].firstEdge = endEdge;
        }else
         {
            while(edge2.nextEdge!=null)
                edge2 = edge2.nextEdge;
            edge2.nextEdge = endEdge;
        }
        Edge edge3 = vertexList[end].firstEdge;
        if(edge3==null)
        {
            vertexList[end].firstEdge = startEdge;
        }else
         {
            while(edge3.nextEdge!=null)
                edge3 = edge3.nextEdge;
            edge3.nextEdge = startEdge;
        }
    }
    
    public void displayVertex(int v)
    {
        System.out.println(vertexList[v].label);
    }
    
    //最开始以vertexList[v]为最小生成树的起点
    public void Prim(int v)
    {
        //存放剩余顶点到当前生成树的最短的一条边的权值
        int lowcost[] = new int[MAX_VERTS];
        int k=0;
        //将vertexList数组下标第v个顶点到其它顶点的所有边当作候选边
        for(int i=0;i<nVerts;i++)
        {
            lowcost[i] = getWeight(v, i);
        }

        //将vertexList[v]并入树中
        vertexList[v].wasVisited = true;
        System.out.println(vertexList[v].label);
        //选中某个顶点后（这里是v）,每次选取剩下顶点中的一个，一共要有nVerts-1个次
        for(int i=0;i<nVerts-1;i++)
        {
            int min = Integer.MAX_VALUE;
            //选出剩下顶点到生成数的最小边
            for(int j=0;j<nVerts;j++)
            {
                if(!vertexList[j].wasVisited && lowcost[j]<min)
                {
                    min = lowcost[j];
                    k=j;
                }
            }
            vertexList[k].wasVisited = true;
            System.out.println("----"+lowcost[k]+"----"+vertexList[k].label);
            //将顶点k并入生成树，并更新剩下顶点到该生成树的最小边
            for(int m=0;m<nVerts;m++){
                //如果剩余顶点到k并入后的生成树的最小边小于并入前的生成树的最小边
                if(!vertexList[m].wasVisited && getWeight(k, m)<lowcost[m])
                    lowcost[m] = getWeight(k, m);
            }
        }
    }
    
    /*
     * 获取边<start, end>的权值；若start和end不是连通的，则返回无穷大。
     */
    private int getWeight(int start, int end) 
    {
        if (start==end)
            return 0;
        Edge currentEdge = vertexList[start].firstEdge;
        while (currentEdge != null) 
        {
            if (end==currentEdge.dest)
                return currentEdge.weight;
            currentEdge = currentEdge.nextEdge;
        }
        return Integer.MAX_VALUE;
    }
}

public class ListUDG_Prim 
{
    public static void main(String[] args)
    {
          UDGraph theGraph = new UDGraph();
          theGraph.addVertex('A'); // 0 
          theGraph.addVertex('B'); // 1
          theGraph.addVertex('C'); // 2
          theGraph.addVertex('D'); // 3
          theGraph.addVertex('E'); // 4
          theGraph.addVertex('F'); // 5

          theGraph.addEdge(0, 1,1); //AB
          theGraph.addEdge(0, 2,4); //AC
          theGraph.addEdge(0, 5,6); //AF
          theGraph.addEdge(1, 3,8); //BD
          theGraph.addEdge(1, 4,3); //BE
          theGraph.addEdge(2, 4,9); //CE
          theGraph.addEdge(2, 5,5); //CF
          theGraph.addEdge(3, 4,7); //DE
          theGraph.addEdge(3, 5,10);//DF
          theGraph.addEdge(4, 5,2); //EF//从0开始，即顶点A开始
          theGraph.Prim(0);
    }
}