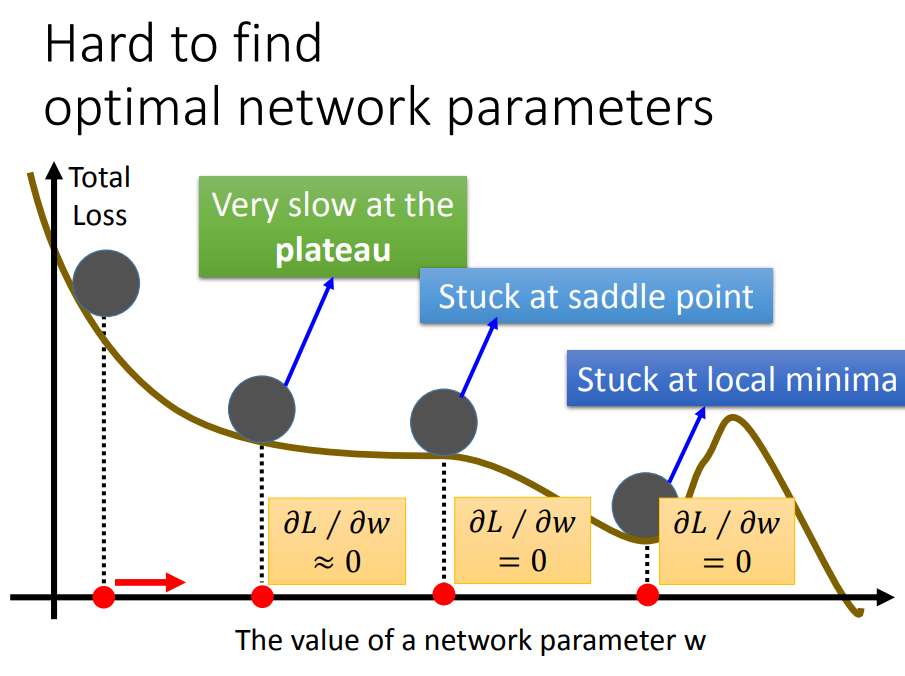
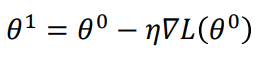Tips of Deep Learning
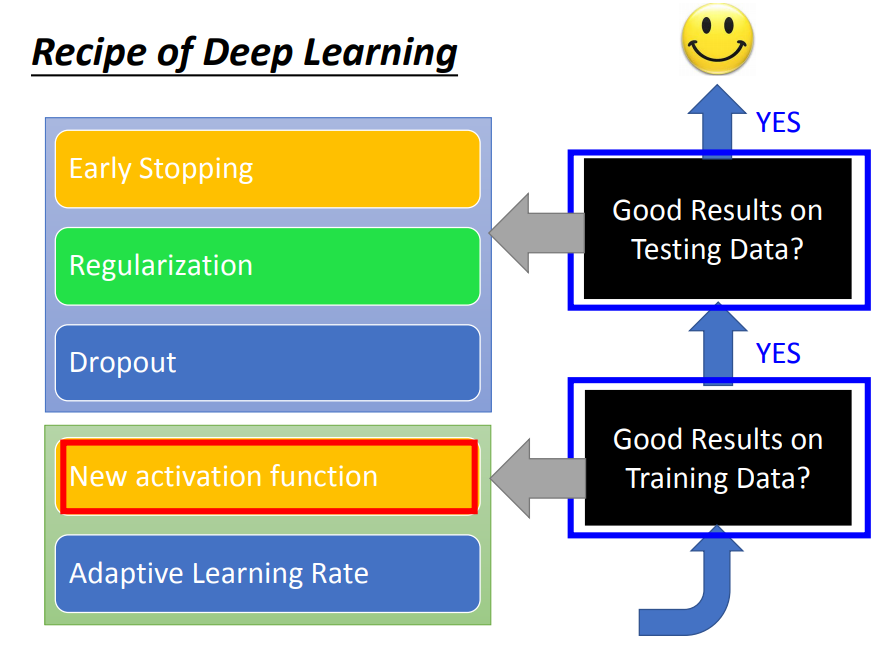
1、先检查training 是否有比较好的结果
training优化方法:
1)换激活函数(Sigmoid、ReLU、Maxout、Tanh、Softmax)
2)优化器——优化gd和自适应调学习率(SGD、Adagrad、RMSProp、Momentum、Adam)
2、training没问题了,再检查testing是否有比较好的结果
testing(过拟合)优化:
1)参数在过拟合之前就停止更新
2)正则化Regularization
3)dropout
1、先检查training 是否有比较好的结果
如果运行模型的时候结果不好,首先看训练结果好不好,而不是一味认为是过拟合
training优化方法:
1)换激活函数(Sigmoid、ReLU、Maxout、Tanh、Softmax)
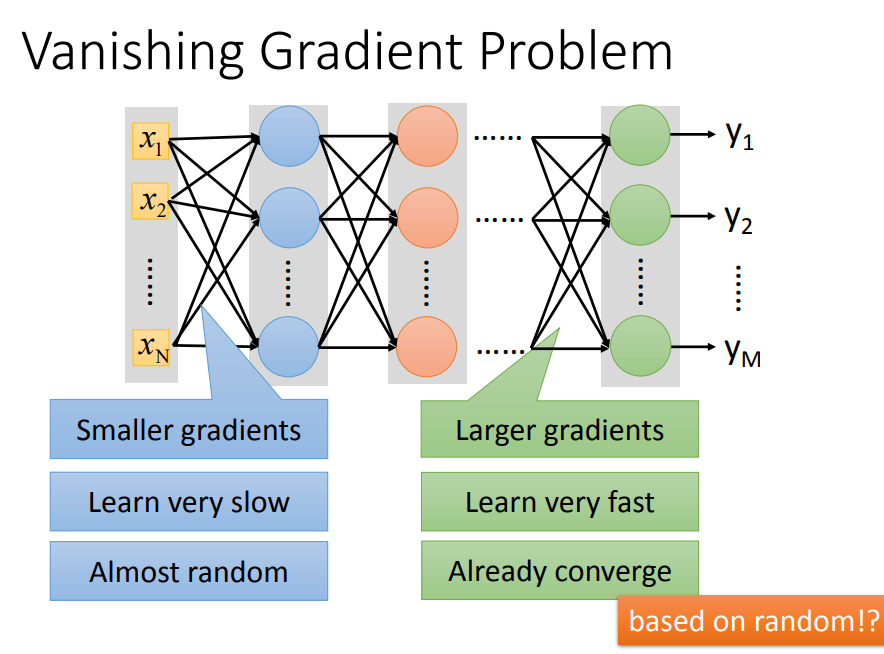
激活函数可能会带来什么样的问题?以sigmoid为例说:会出现梯度消失
一、什么是梯度消失
- 有梯度时,参数才会往梯度最小的地方改变;没有梯度了,参数就停止更新了。
- 前面层的学习速率明显低于后面层(后向传播),这就是梯度消失。
二、为什么会出现梯度消失
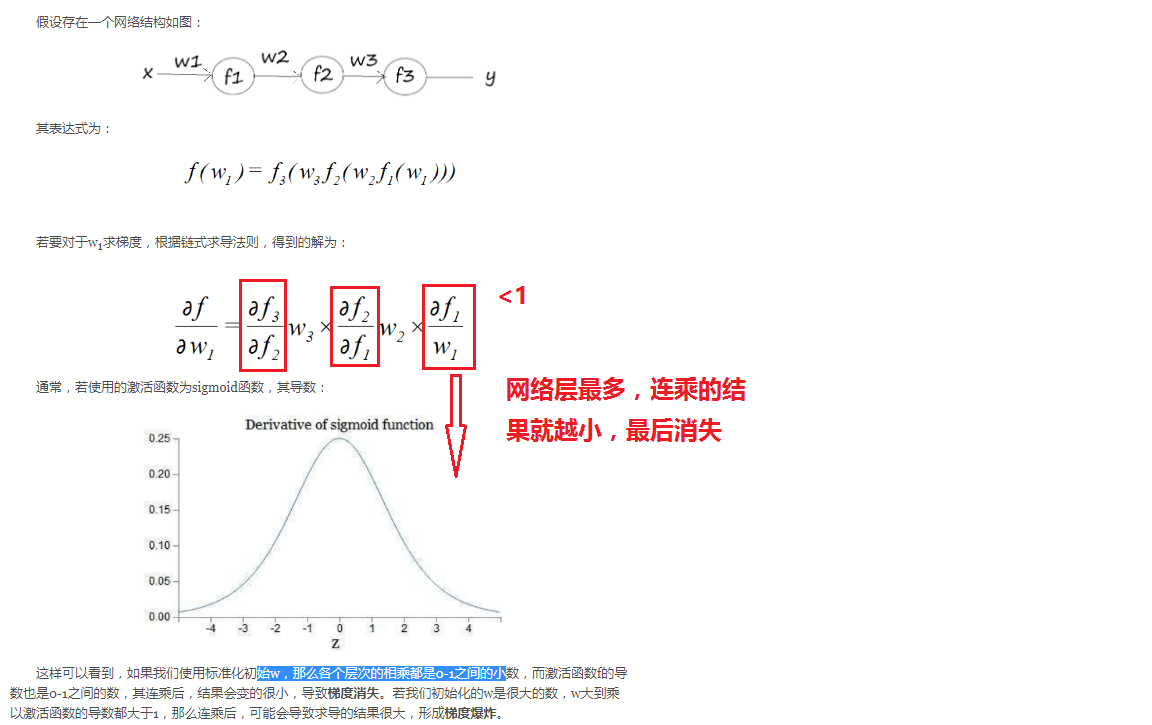
三、如何解决梯度消失问题——换激活函数
梯度消失是因为sigmoid引起的,要解决当然要换一个激活函数。
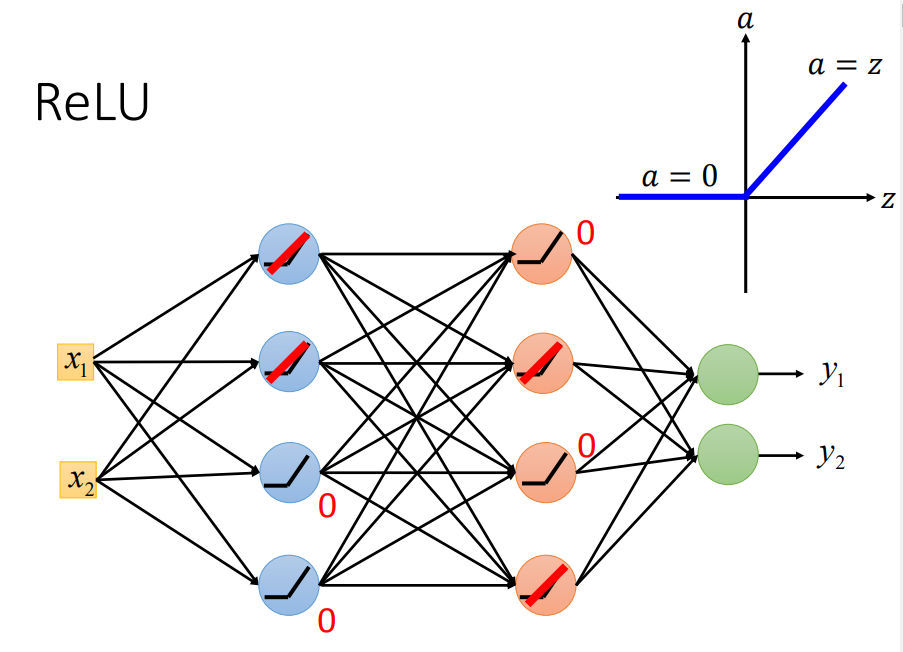
1、换ReLU
input<0时,输出为0,input>0,输出为原值

ReLU还可以令神经网络更加thinner
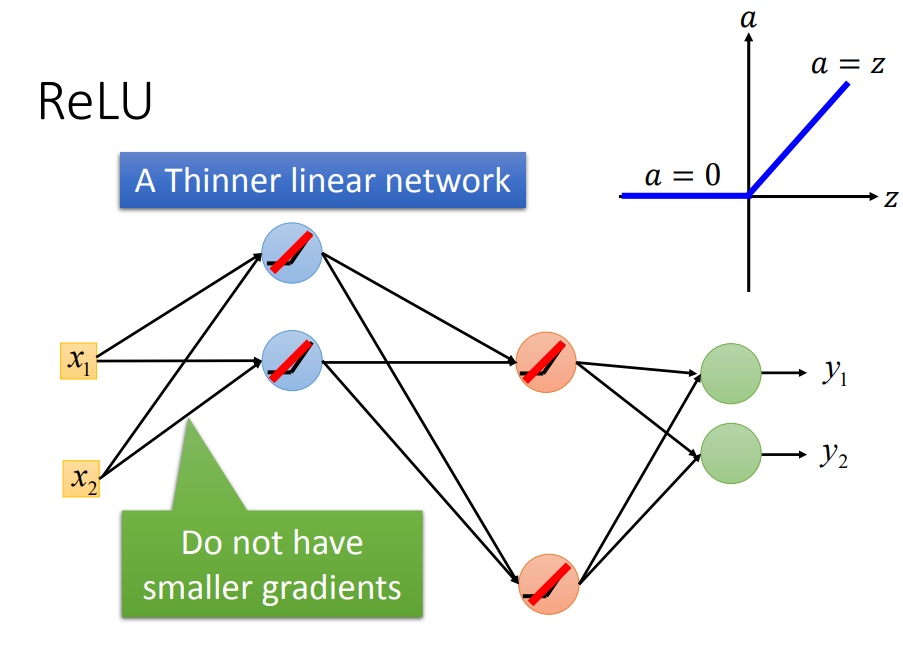
ReLU只是在微小范围内线性的,整体是非线性的(因为只要输入有比较大的变化时,ReLU都会不同)
ReLU变形:
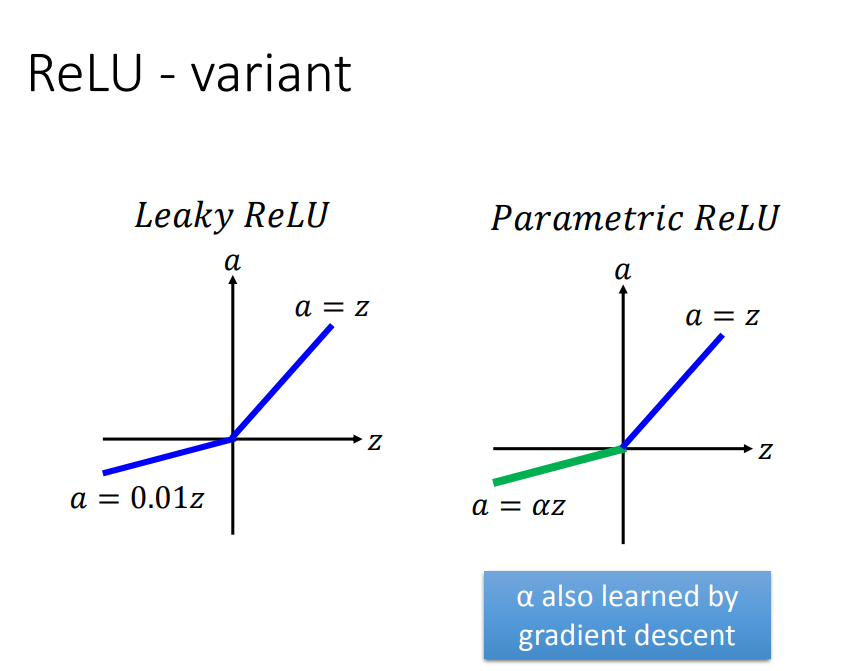
2、Maxout(ReLU增强)——能自动学习激活函数(随着参数更新,激活函数一直改变)
一、首先看看Maxout的结构(多了一个max):
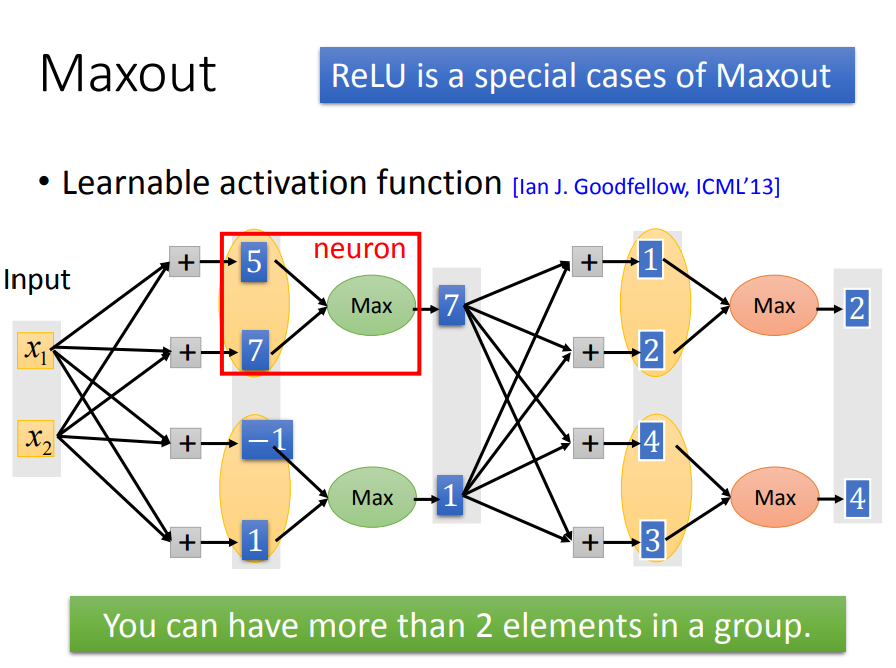
二、然后,maxout是如何自动调整激活函数呢(也就是随着参数更新,激活函数一直改变)
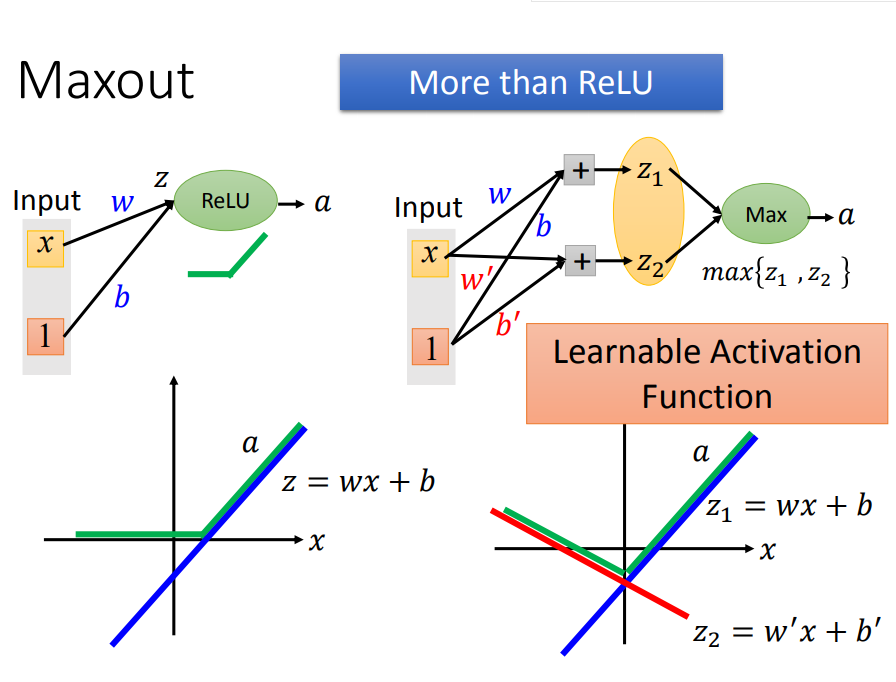
w,b不同时,激活函数就不同(右边)。当w`和b`为0时,激活函数就会变成ReLU(左边),当输入有3个element时,激活函数就会有3段

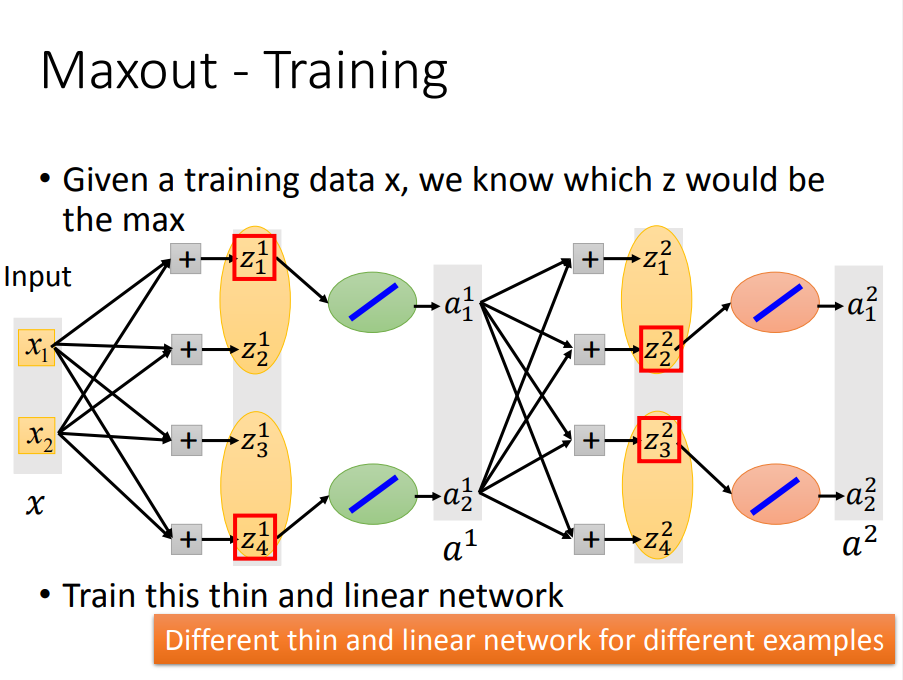
三、那么maxout是如何 train data呢
max选择了哪一个较大参数的路,就用该激活函数那段来求偏导
2)优化器——优化gd和自适应调学习率(SGD、Adagrad、RMSProp、Momentum、Adam)
利用梯度下降的方法update数据,其决定因素主要是 梯度值 和 学习率eta 两个因素
Tip1:SGD(updata数据会更快)

Tip2:Feature Scaling
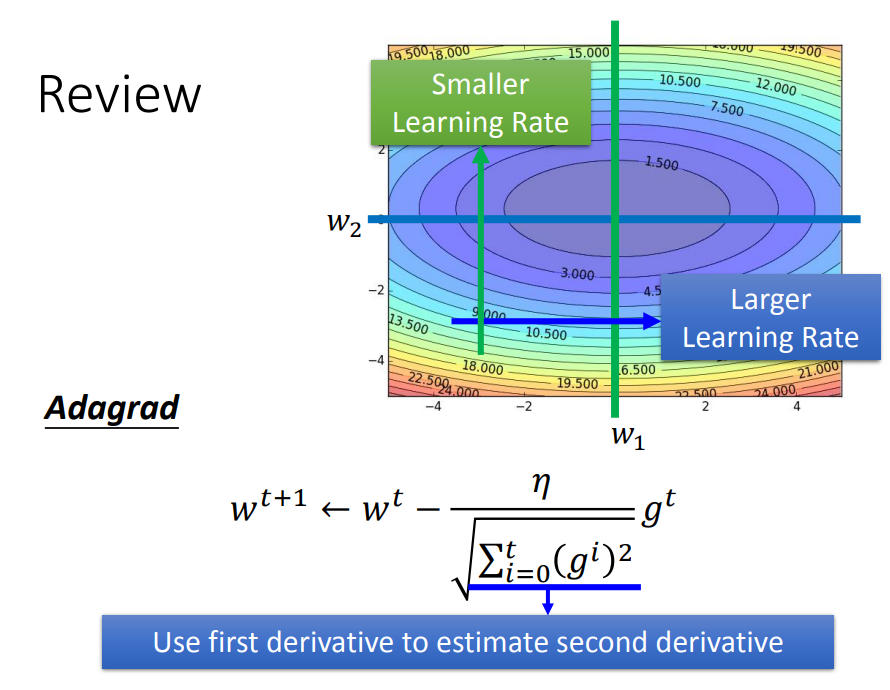
Tip3:Adagrad
learning rate小了,训练速度会很慢,learning rate大了,训练就得不到好结果,那么应该要自适应调节才行。
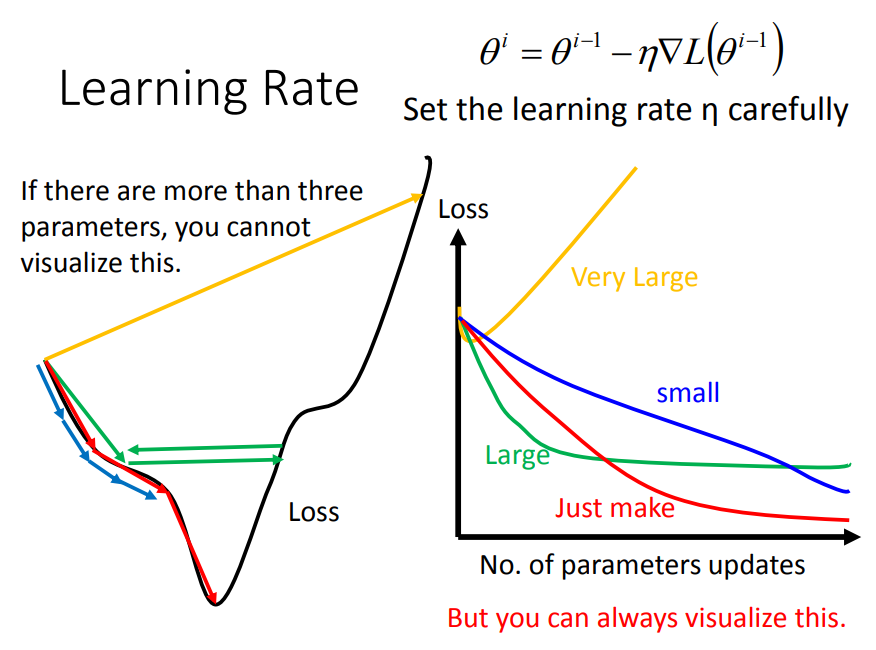
一、如何自适应
前面说到,利用梯度下降的方法update数据,其决定因素主要是 梯度值 和 学习率eta 两个因素
那么我们的目标是:学习率eta从大——>小,梯度从大——>小变化,训练正常的话梯度是由大到小变化的,那么如何让eta也从大到小变化呢(除以一个梯度的均方根)


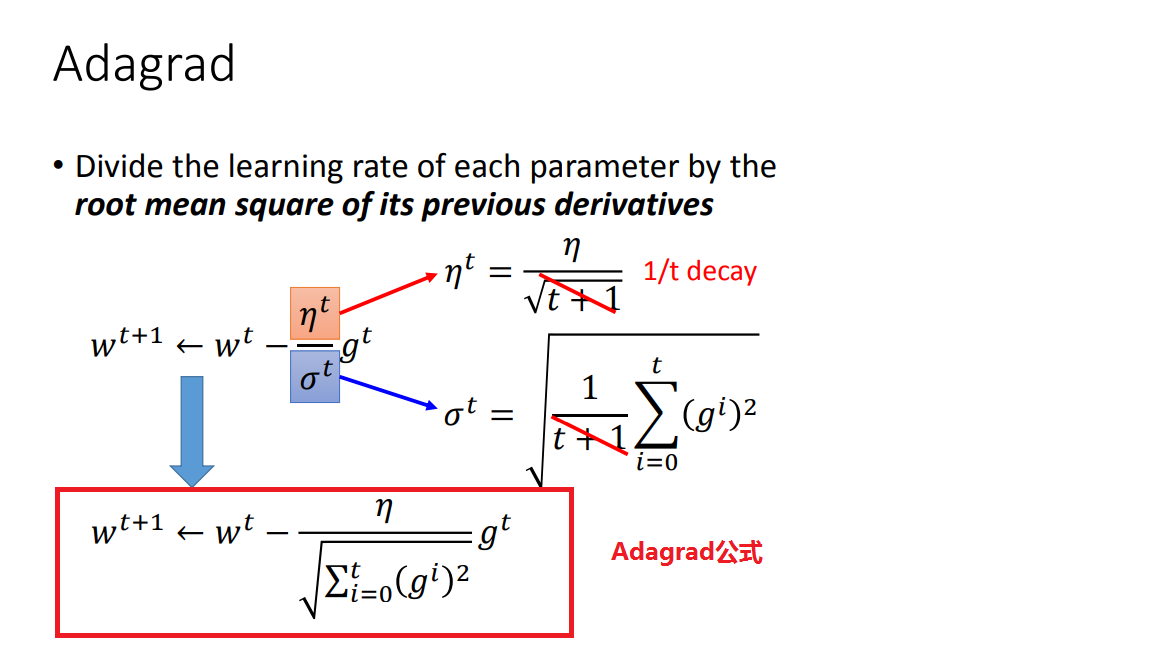
这样,随着梯度累计越来越多,eta就会越来越小,实现了eta由大到小的变化。但是为什么要除以一个梯度的均方根呢,这样做有什么道理的吗?
二、为什么要除以一个梯度的平方和开根号
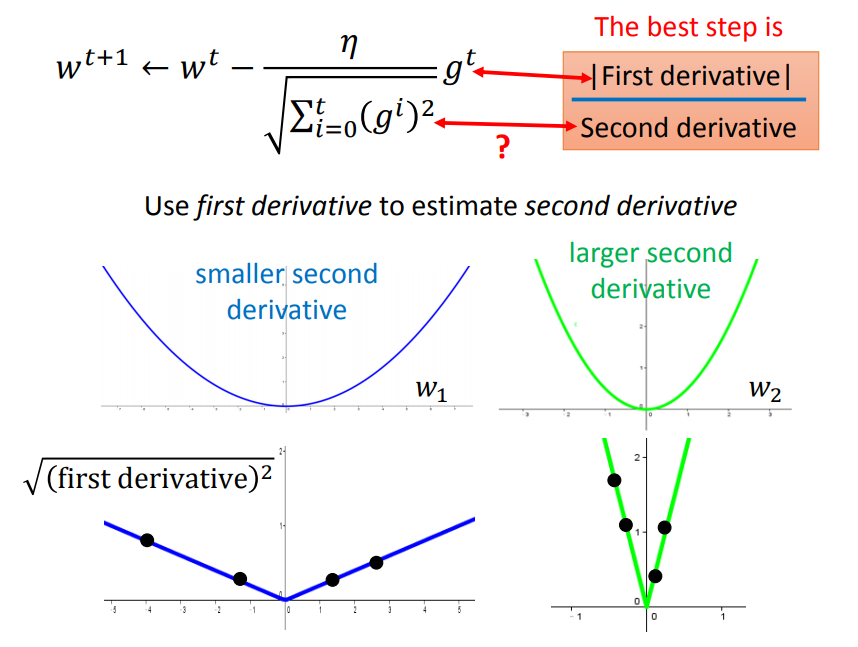
我们用一个简单的例子说明,假如要从以下二维函数的一点到达最低点,那么最佳的step应该是跟一次导数(梯度)有关的:
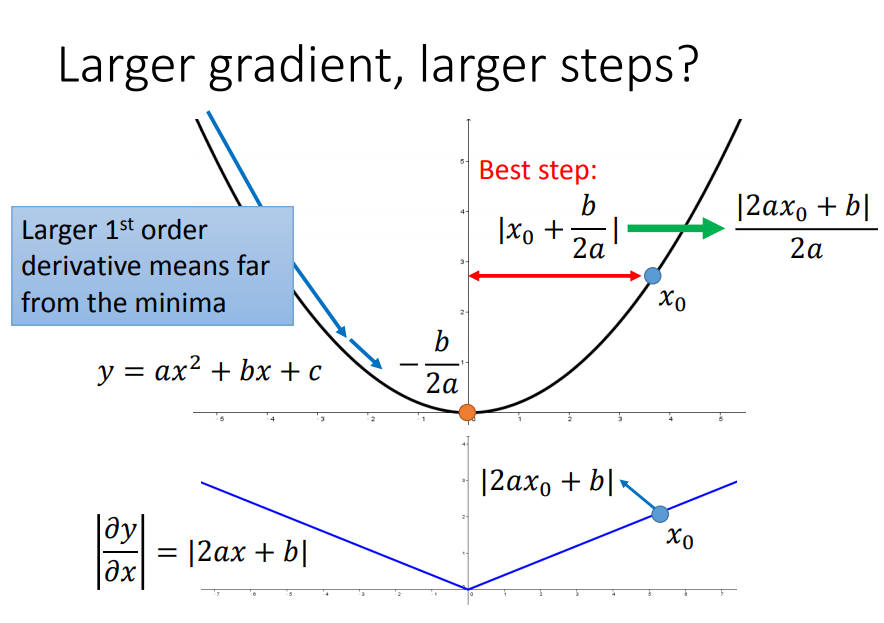
但是单单考虑一次导数是不够的,要是在三维函数里面就不行了:(比如要判断出a、c哪个离最低点近,该给一个大一点还是小一点的eta比较合适)
这时候要引入二次导数:
绿色曲线的曲率大一点,所以二次导数更大,所以虽然c的一次导数比较大,但是由于二次导数也大,综合影响c点离最低点比较近,给一个小一点的eta就可以了
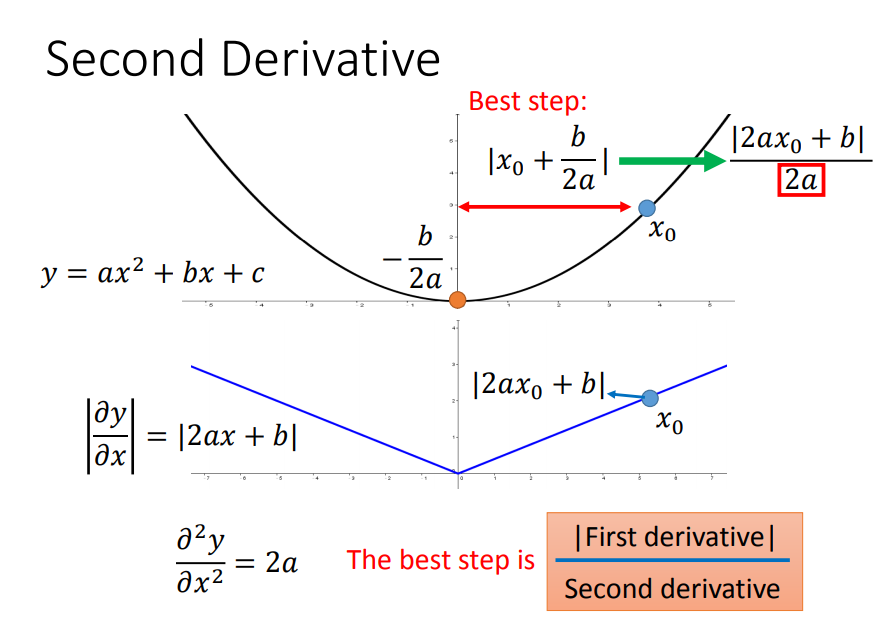
综上,用梯度的平方和开根号近似于二次导数(因为曲线越宽,曲率越小,很多梯度的平方和就越小,因此二次微分就越小),就得到了Adagrad公式了
Tip4:用RMSProp
一、为什么要用RMSProp
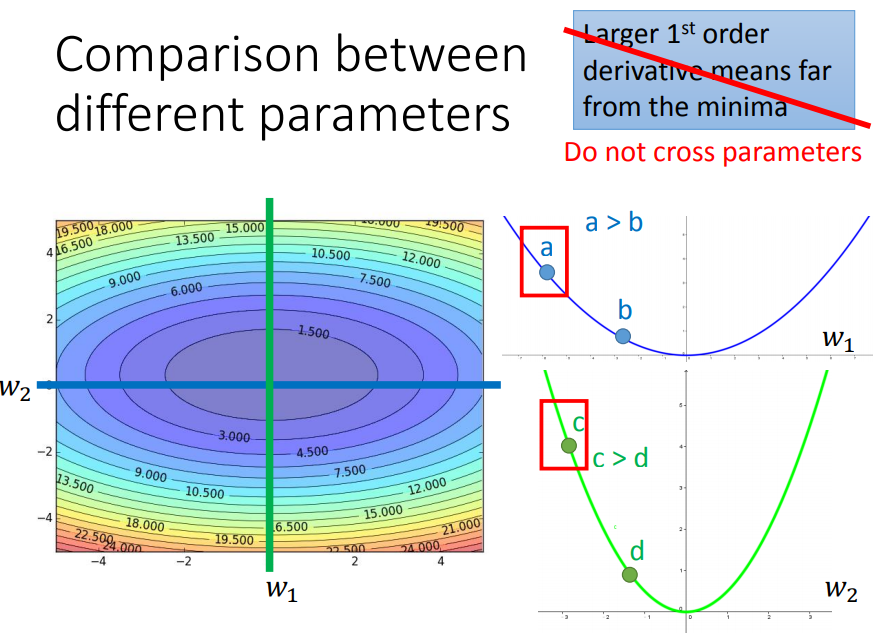
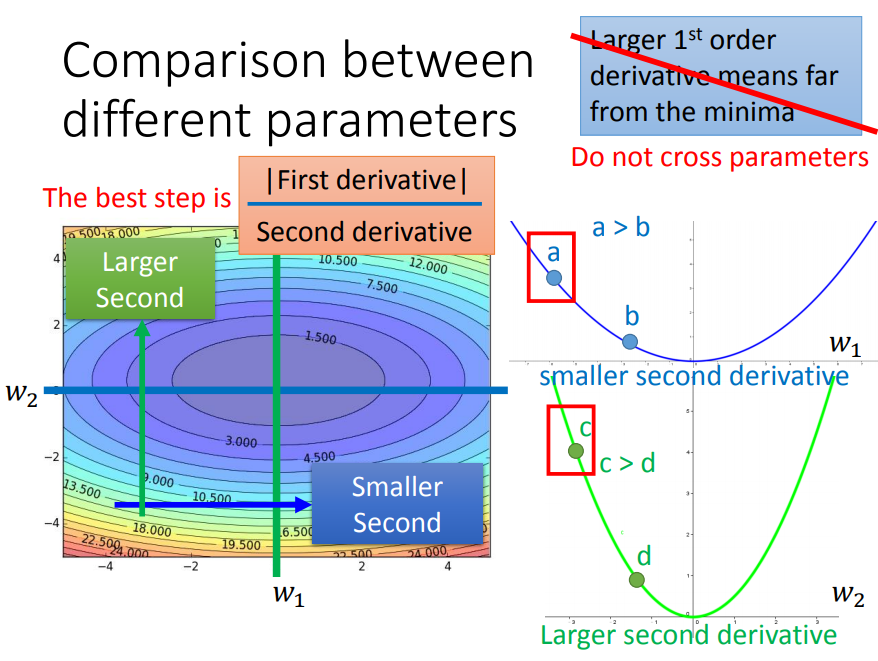
在上面Adagrad中,学习率是跟损失函数对w的二次微分有关。那么对于图中蓝绿相交的一点来说,因为w1所在的曲率相对于w2要小,所以w1的学习率会比w2大。现在单考虑w1(只看横向),那么二次微分是固定的(碗状),也就是说w1是根据固定的规则去自动调整eta的。但是现实中同一方向的二次微分是不固定的,因此对于同一方向W1,需要不同的规则去调eta。
对于一个参数来说,Adagrad是用固定的规则去调eta,RMSProp是用变化的规则去调eta
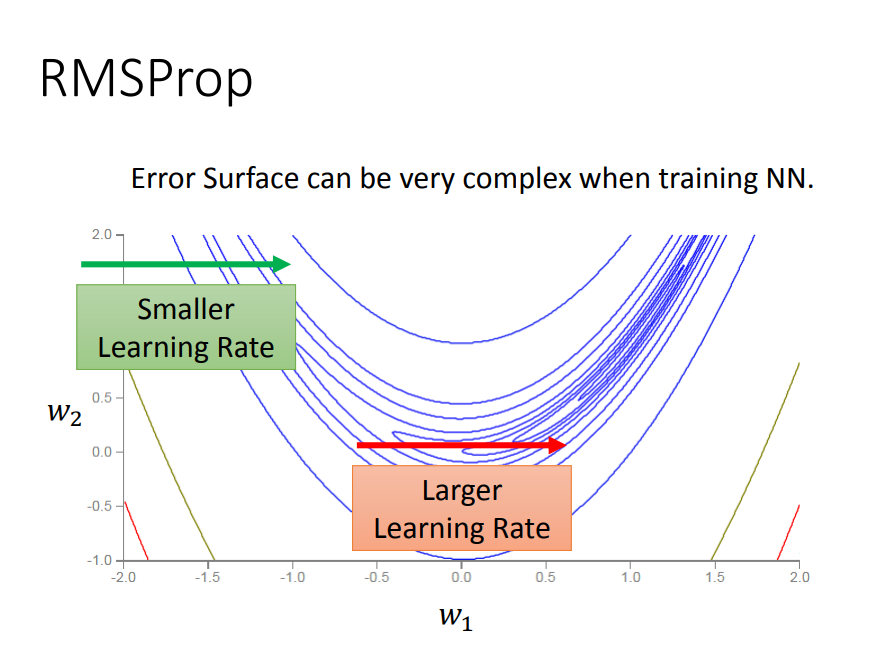
二、如何实现RMSProp
在原来分母这一项中,在过去梯度平方和前面加上权值a,现有的梯度平方加上1-a。
使用指数衰减滑动平均以丢弃遥远过去的历史(在参数空间更为平缓的方向,会取得更大的进步(因为平缓,所以历史梯度平方和较小,对应学习下降的幅度较小),并且能够使得陡峭的方向变得平缓,从而加快训练速度)

Tip5:Momentum
一、Momentum(动量)是解决局部最小值问题的
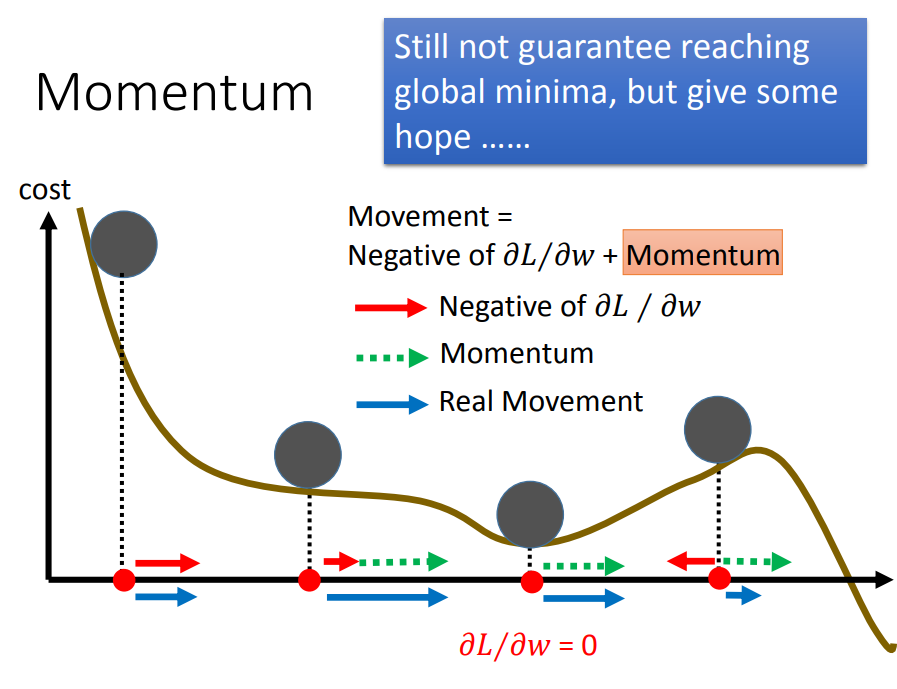
二、如何实现Momentum
· 
Tip6:Adam(RMSProp+Momentum)

2、training没问题了,再检查testing是否有比较好的结果
testing(过拟合)优化:
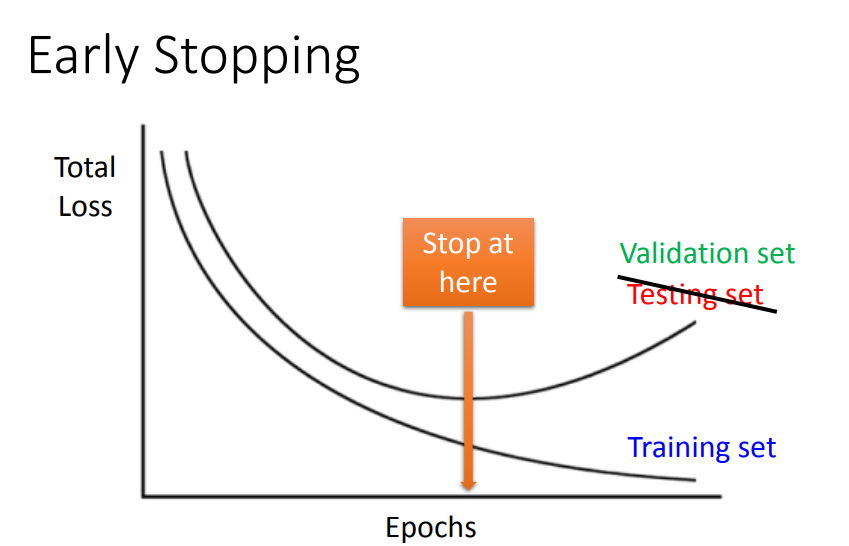
1)参数在过拟合之前就停止更新
由于在test之前是不知道testing的表现的,所以也就不知道如何找到这一个过拟合前的临界点,因此需要在training data中划分一笔validation data来确定这个点。
2)正则化Regularization
正式引出传说中的L1、L2(范数)正则化
一、首先理解什么是范数,L1(范数为1)和L2(范数为2)是什么
范数:向量在不同空间中“长度”的计算公式
L1:绝对值之和
L2:平方和
二、L2正则化(权值衰减)
1)首先,L2是如何权值衰减的

因为η、λ、n都是正的,所以 1−ηλ/n小于1,它的效果是减小w,这也就是权重衰减(weight decay)的由来。当然考虑到后面的导数项,w最终的值可能增大也可能减小。
2)然后,为什么参数w衰减能防止过拟合
模型过于复杂会导致过拟合。那么越小的w(可以想象成0理解),表示网络复杂度低,越简单的网络结构,就越不会过拟合。
比如模型 y=W1*X1+W2*X22 中把w2=0代入,模型就会简化,就不会引起过拟合
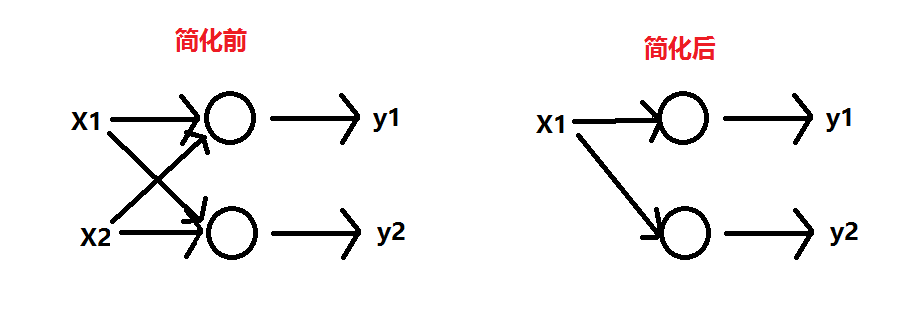
3)最后,总结(我的理解)正则化防止过拟合的本质:减少“没用参数”的权值(防止过拟合),同时也减少“有用参数”的权值(会增加bias误差)
什么是有用参数,什么是没用参数?如2)中,怎么就把x2删去,不把x1删去呢?
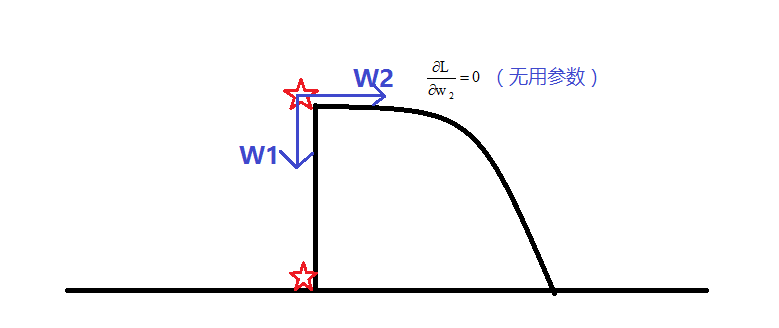
我们姑且假设w1是有用参数,w2是无用参数,由公式知参数更新值跟权值、梯度值两个因素有关,实际上,无论是x1还是x2,权值都会衰减,每update一次参数,权值w就会衰减一次,但如果是下图的情况,损失函数Loss的减少跟w2没关系的,所以对其偏导为0,那么w2的参数更新只跟权值有关了,随着更新次数叠加,权值就会逐渐衰减接近0;对于有用参数w1,虽然它权值衰减,但是它其作用的是后面的偏导值,所以它还是不会变成0的。
三、L1正则化
L1是在Loss函数加上绝对值之和,求偏导后比原始的更新规则多出了η * λ * sgn(w)/n这一项。当w为正时,更新后的w变小。当w为负时,更新后的w变大——因此它的效果就是让w往0靠,使网络中的权重尽可能为0,也就相当于减小了网络复杂度,防止过拟合

3)dropout
dropout也是为了简化神经网络结构的目的,但L1、L2正则化是通过修改代价函数来实现的,而Dropout则是通过修改神经网络本身来实现的。
一、dropout是如何实现的
1、在training的时候,每次update参数之前,对每一个Neuron(包括input_layer)做sampling,决定这个Neuron按一定几率p丢掉,跟它相连的weight也被丢掉,结果得到一个细长的Network。(每一次update一个mini-batch之前,拿来traing的Network structure是不一样的)

在testing的时候,注意:1 、不做dropout,2、如果training时的删除神经元的概率为p%,则在testing时,所有的weight都要乘以(1-p)%
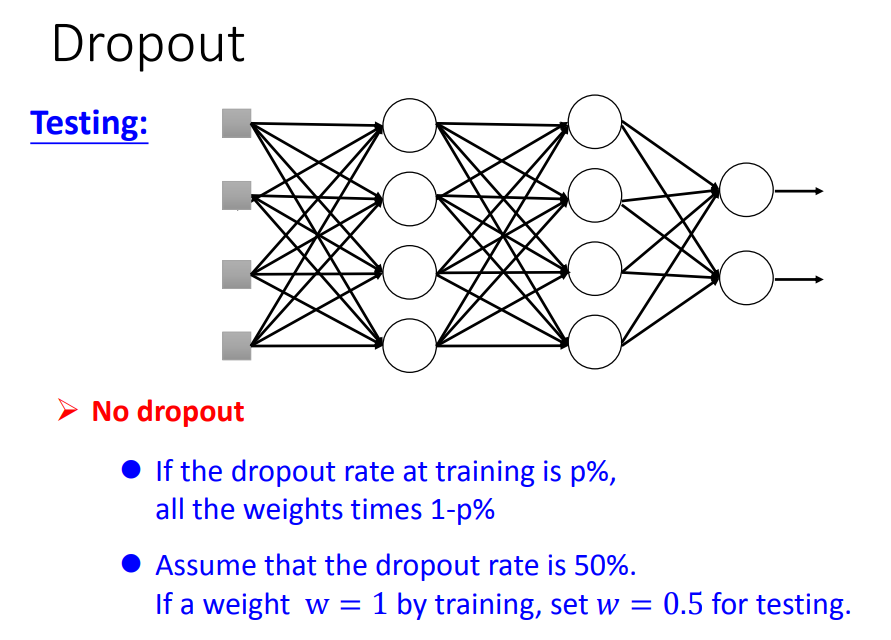
二、dropout的原理(为什么这样做可行)
回顾正则化原理:通过修改代价函数最终也是为了实现简化模型的,dropout就更加直接!
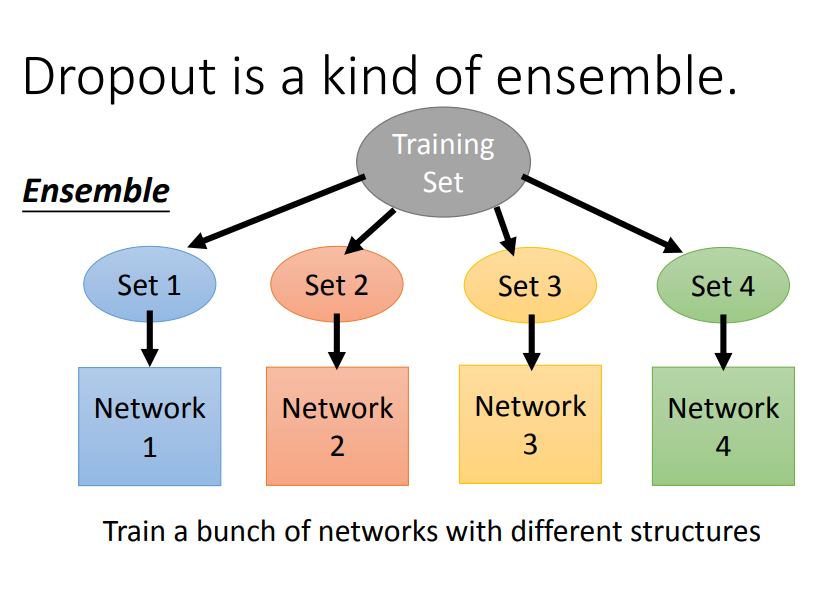
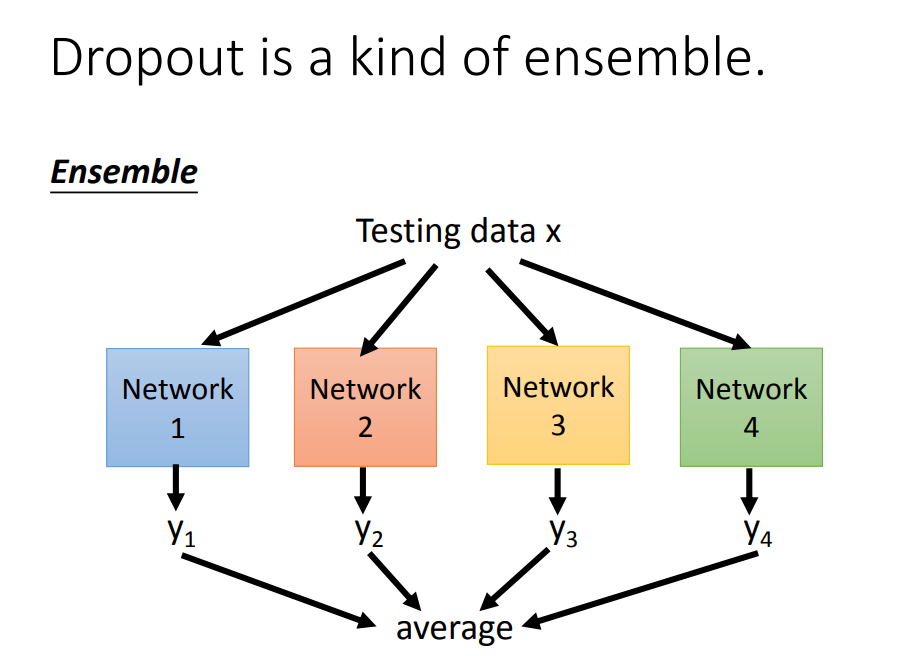
实际上,dropout是利用ensemble思想,把一个复杂神经网络的训练转化为,训练很多个简单的神经网络,然后再把多个简单神经网络训练出来的参数做平均
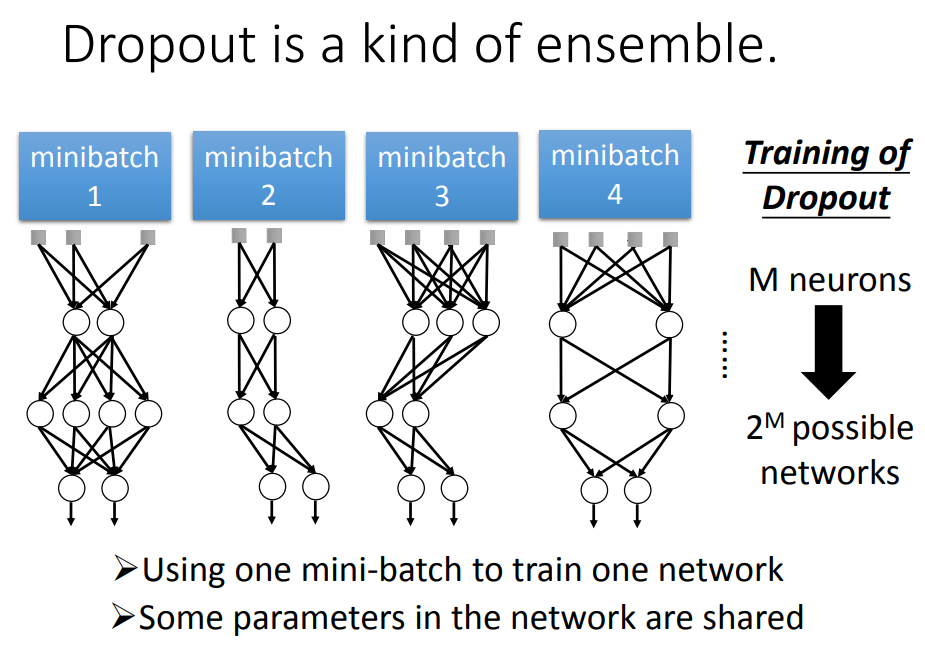
testing的时候也一样操作:
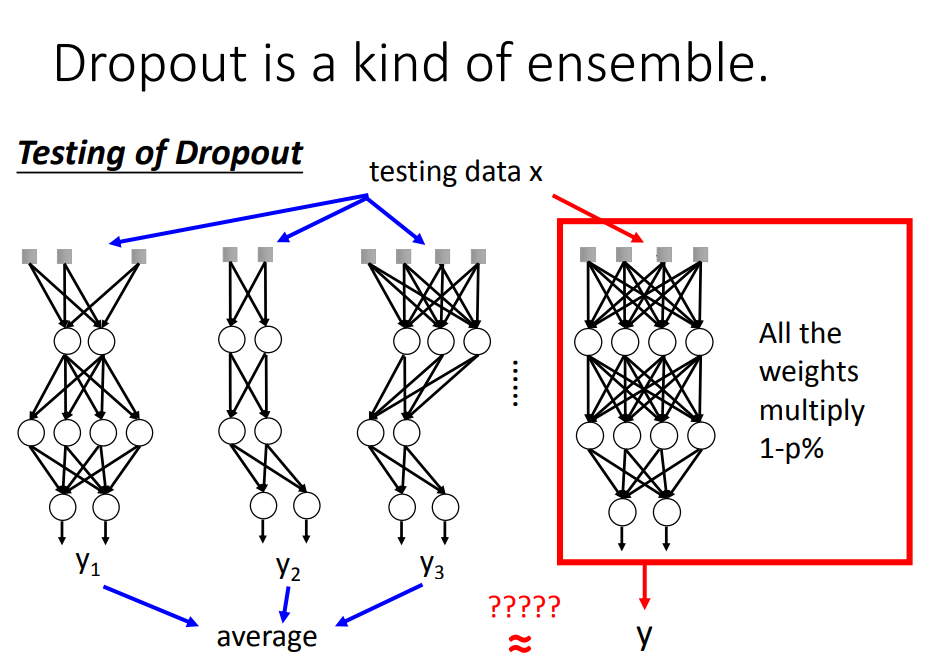
最后,testing中dropout的过程就可以用权值*(1-p)%来代替