model的误差来源分析
思路:
1、首先,error的两大来源bias和variance是指什么
2、然后,bias和variance是怎么产生的
3、进一步,如何判断你的model是bias大(欠拟合)还是variance大(过拟合),如何解决
4、最后,结论
1、首先,error的两大来源bias和variance是指什么

1)、我们知道,不同的model对于同一个training data和同一testing data的performance都是不同的,
并不是说越复杂的model就会表现得越好,那么误差来源于哪里呢?
误差的两大来源:bias和variance
2)、什么是bias和variance呢?
首先知道什么是误差:前面的学习知道,机器学习就是寻找一个函数,然后给它一个输入,就能得到一个理想的输出。
f head是理论上找到的最佳函数,f star 是我们用模型预测出来的函数,两者的差值就是误差。
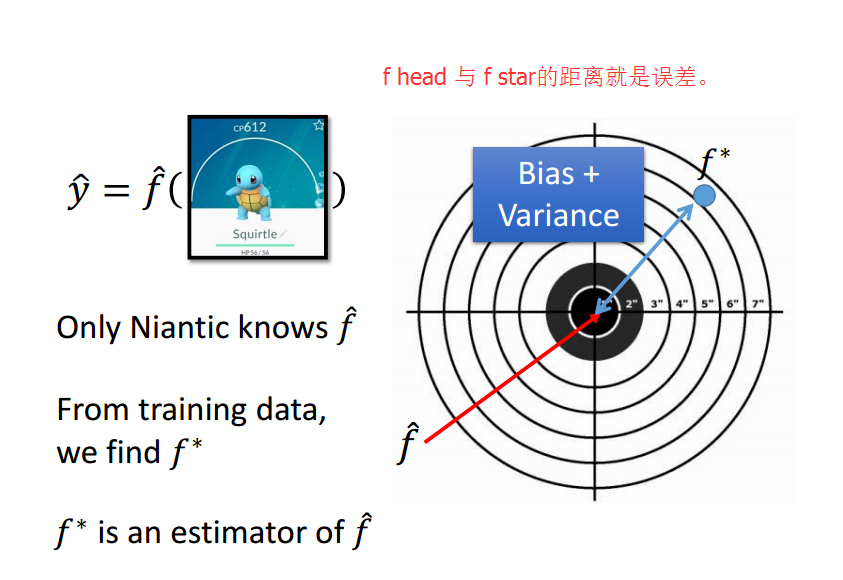
接着,我们来看看什么是bias和variance(偏差和方差):
举个栗子说明,下图是用一定样本数的均值m来估计假设的随机变量的平均值u,这是一种无偏估计(unbiased)。

也就是说,估计值的期望等于假设值(如上文的E(m)=u),即为无偏差,反之有偏差(bias)。
当样本数越来越大时,m就越靠近u。
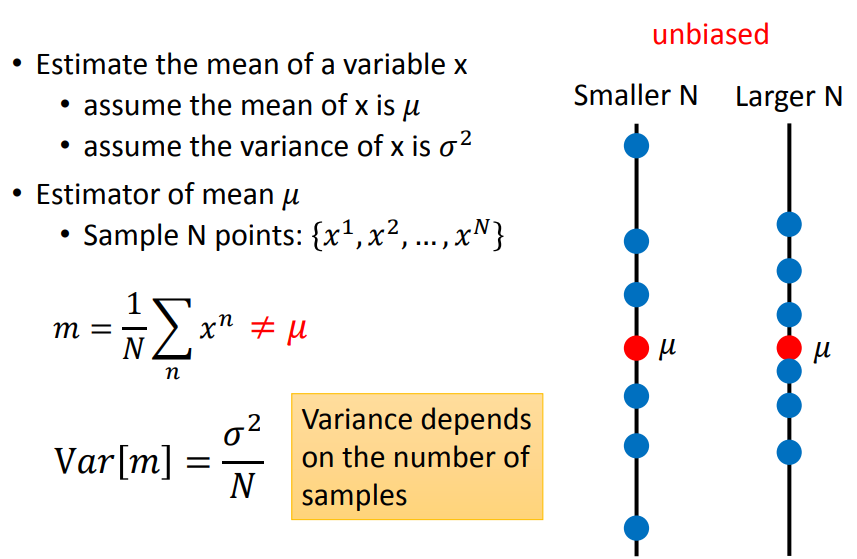
方差表达的是数据的离散程度,这里对于方差的估计是有差估计:

最后,bias和variance的直观理解:
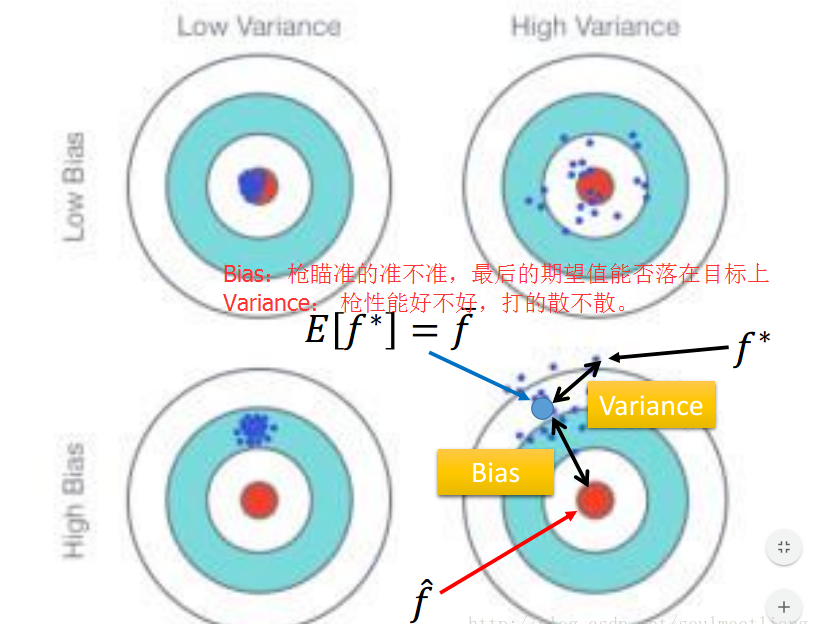
因此,bias表示的是预测的f bar(预测f star的期望)与f head的距离,variance表示的是每次预测的f star 与f bar的距离(看图)
2、然后,bias和variance是怎么产生的
下面结合实际的实验说明,bias和variance是如何产生的。
由上述得出,我们要知道bias有多大,就要做多次实验,确定多个f star,然后求出f star期望(E(f*))
那么首先,我们可以设计100组实验,每组实验10个数据,如下图:
然后思考,对于这样的数据,我们选用什么model比较好呢,哪一个model最后的bias比较小呢?
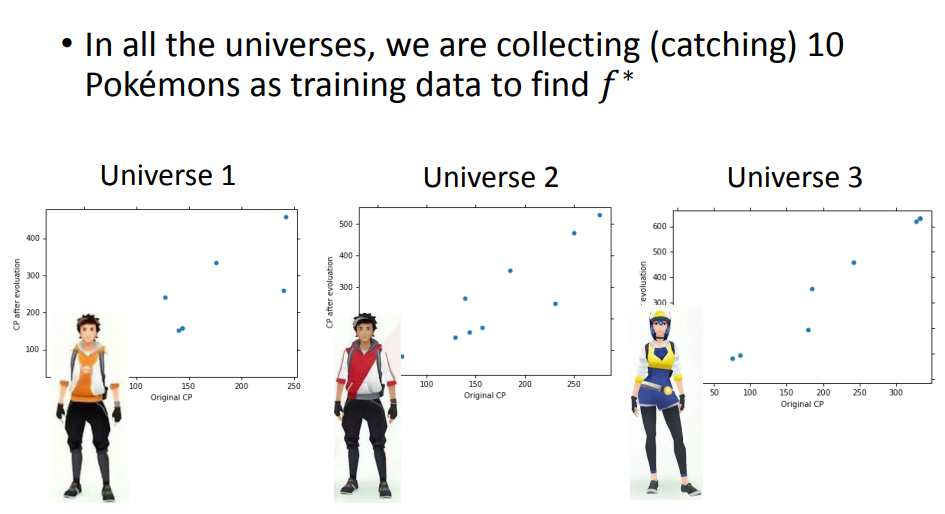
接着,我们就开始比较不同model的performance,比如先用一个一次model,就得到了100个不同的 f star(model参数不同)
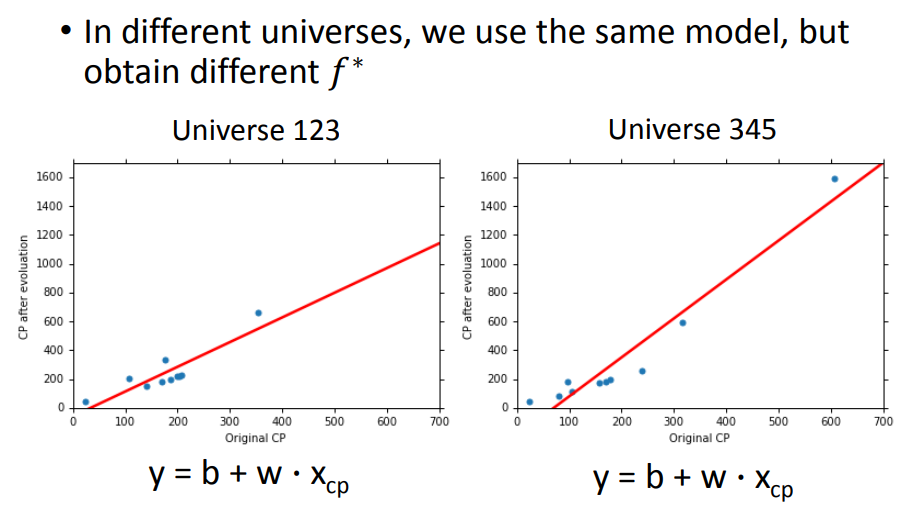
进一步可以比较,不同的model中(每种model有100个f star)的表现:
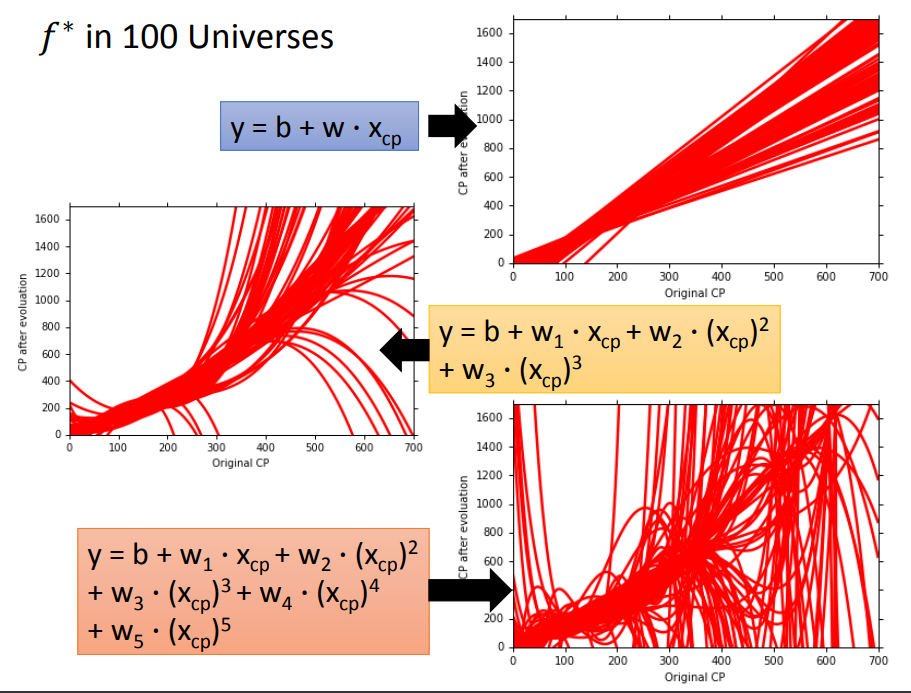
有了很多不同的 f star 之后,就可以求出期望,与假设的 f head对比,就得到bias了!!
于是,bias和variance就产生了!
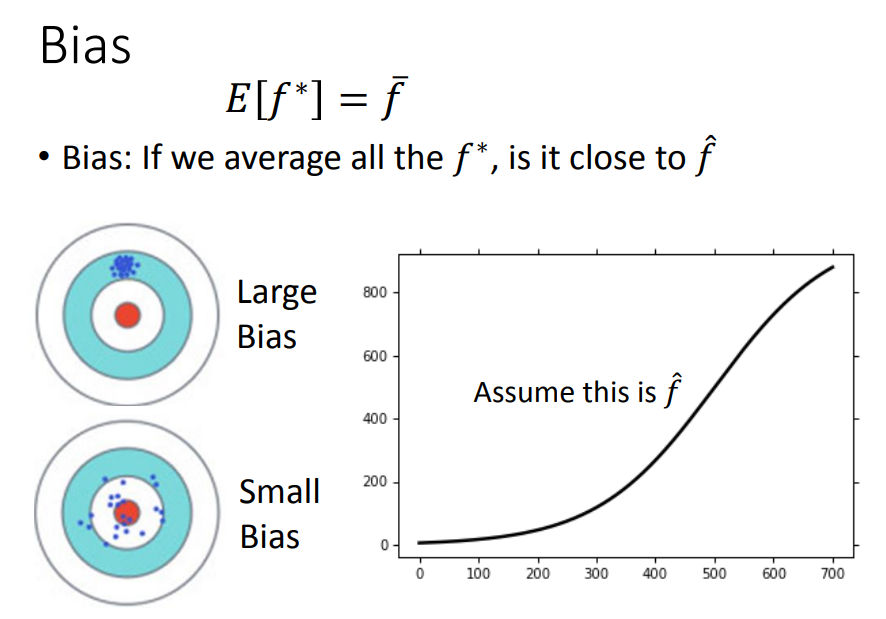
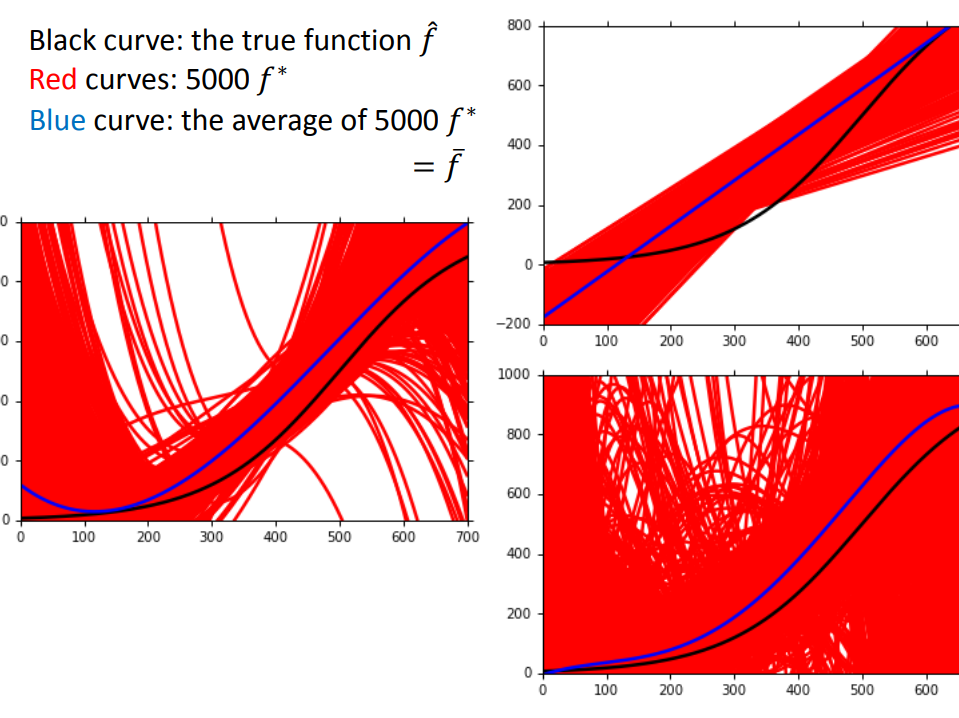
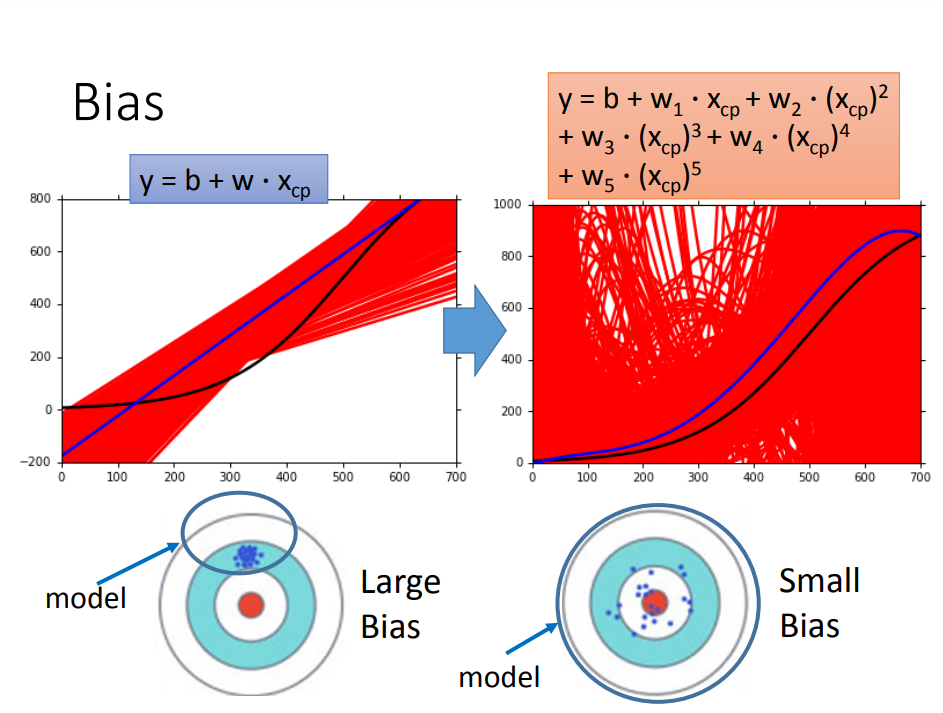
图中看出,简单model可能并不包含目标,因此会造成较大的bias
variance的产生是在测试数据集的时候发现训练出来的function有很大的误差,此时variance就产生了
(是因为训练出来的function太扭曲了)
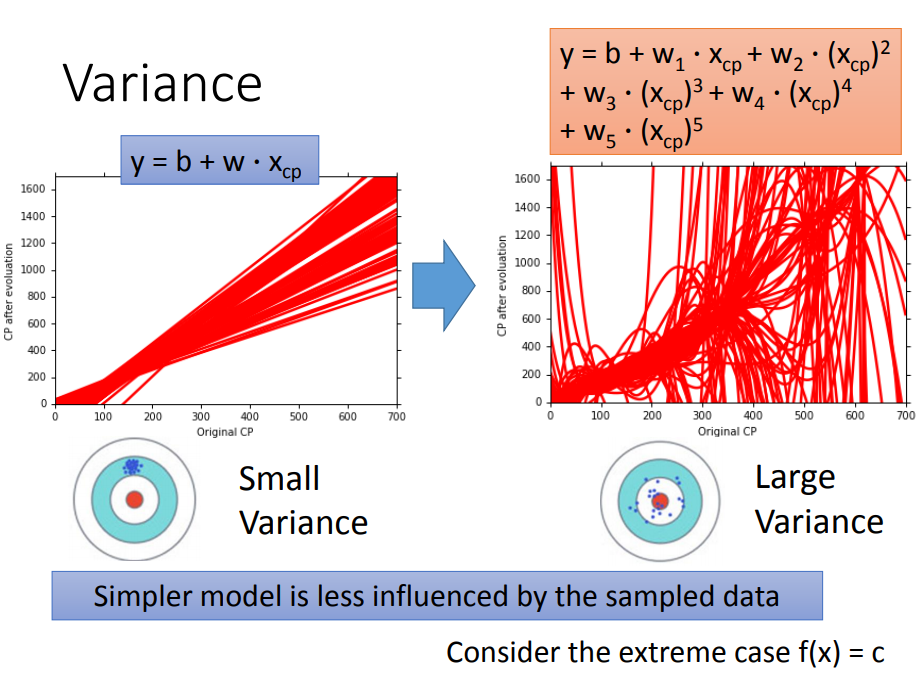
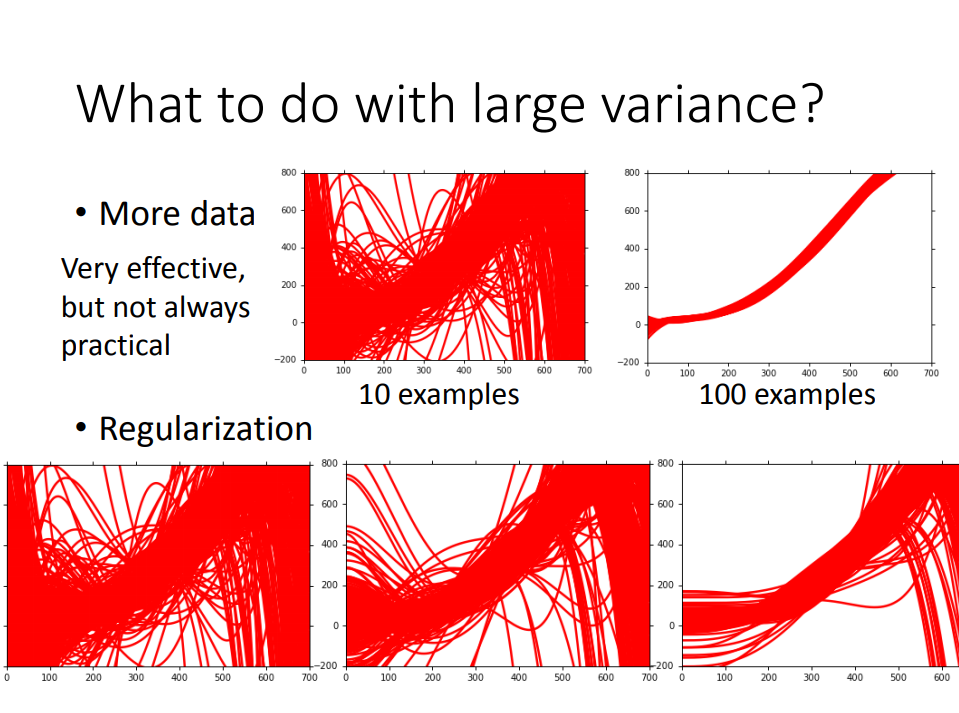
最后我们可以解释一开头的图片,得到结论:我们理想中的目标是找到一个平衡点,使bias和variance尽可能小。
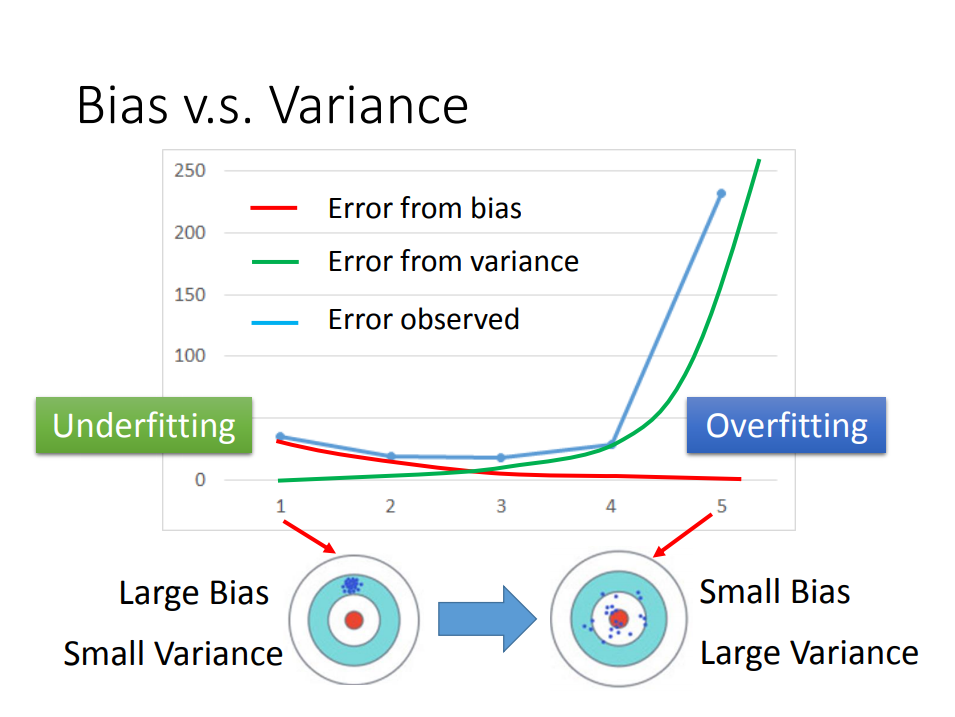
3、进一步,如何判断你的model是bias大(欠拟合)还是variance大(过拟合),如何解决