迪杰斯特拉算法（戴克斯特拉算法）（Dijkstra算法）-贪心、最短路径问题

戴克斯特拉算法：（英语：Dijkstra's algorithm，又译迪杰斯特拉算法）由荷兰计算机科学家艾兹赫尔·戴克斯特拉在1956年提出。戴克斯特拉算法使用了广度优先搜索解决赋权有向图的单源最短路径问题。

如图为一个有权无向图，起始点1到终点5，求最短路径

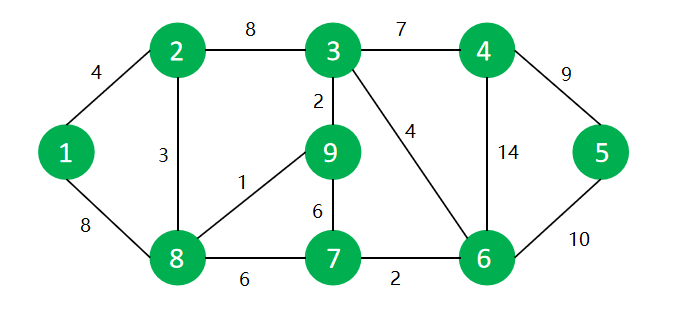
 lowcost数组存储下标点到起始点的最短距离，mst数组标记该点是否已标记，

如下图，遍历graph数组找出初始点（点1）与个点之间的距离存入lowcost（距离<lowcost存入），*为无穷大

遍历lowcost数组，找出最小值并且没有被标记过（mst != 0），找出的最小值的点标记（mst = 0），sum=4

遍历graph数组，存入lowcost中（注意：8到2的距离+sum<lowcost[8]，所以lowcost[8]=graph[2][8]+sum） 注意：mst[1]是等于0的，下面都是0

 

 遍历lowcost数组，找出最小值，sum=7

以下都依次类推...

  

 

 

 

 

 

 

 

 

 

输入：

9 14 1 5
1 2 4
1 8 8
2 8 3
2 3 8
8 9 1
8 7 6
3 9 2
9 7 6
3 4 7
3 6 4
7 6 2
4 6 14
4 5 9
6 5 10

输出：

24

代码：

#include <iostream>
#include <bits/stdc++.h>
using namespace std;

#define MAX 100
#define MAXCOST 0x7fffffff  //int型最大值

void prim(int graph[][MAX],int n,int start,int end)
{
    int lowcost[MAX];
    int mst[MAX];
    int sum=0;
    for(int i=1;i<=n;i++)//将与各点与起始点的距离存入lowcost中
    {
        lowcost[i]=graph[start][i];
        mst[i]=1;
    }
    mst[start]=0;  //起始点被标记
    for(int i=1;i<=n;i++)
    {
        if(mst[end]==0)//终点被标记结束
        {
            cout<<sum;
            break;
        }
        int min=MAXCOST;
        int minid=0;
        for(int j=1;j<=n;j++)//遍历lowcost数组，找最小值
        {
            if(lowcost[j]<min && mst[j]!=0)
            {
                min=lowcost[j]; //最小值
                minid=j; //最小值下标
            }
        }
        //cout<<"V"<<mst[minid]<<"-V"<<minid<<"="<<min<<endl;
        sum=min;
        //cout<<sum<<endl;
        mst[minid]=0;  //最小值下标点被标记
        for(int j=1;j<=n;j++)//找最小值点与各点的距离
        {
            if(graph[minid][j]==MAXCOST)//如果此点与最小值点没有联系（距离为最大值）则lowcost不变，跳过
            {
                continue;
            }
            else if(graph[minid][j]+sum<lowcost[j] && mst[j]!=0)//此点与最小点有联系，并且+sum<lowcost 并且此点没有被标记，则赋值给lowcost
            {
                lowcost[j]=graph[minid][j]+sum;
            }
        }
    }
}
int main()
{
    int n,m;
    int start,end;
    int graph[MAX][MAX];
    cin>>n>>m>>start>>end;
    //初始化图G
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            graph[i][j]=MAXCOST;
        }
    }
    //构建图G
    for(int k=1;k<=m;k++)
    {
        int i,j,cost;
        cin>>i>>j>>cost;
        graph[i][j]=cost;
        graph[j][i]=cost;
    }
    prim(graph,n,start,end);
    return 0;
}