克鲁斯卡尔算法（Kruskal算法）（最小生成树算法）-贪心

克鲁斯卡尔算法：Kruskal算法是一种用来查找最小生成树的算法，由Joseph Kruskal在1956年发表。用来解决同样问题的还有Prim算法和Boruvka算法等。三种算法都是贪心算法的应用。和Boruvka算法不同的地方是，Kruskal算法在图中存在相同权值的边时也有效。

基本思想：先构造一个只含 n 个顶点、而边集为空的子图，把子图中各个顶点看成各棵树上的根结点，之后，从网的边集 E 中选取一条权值最小的边，若该条边的两个顶点分属不同的树，则将其加入子图，即把两棵树合成一棵树，反之，若该条边的两个顶点已落在同一棵树上，则不可取，而应该取下一条权值最小的边再试之。依次类推，直到森林中只有一棵树，也即子图中含有 n-1 条边为止。

发现一个好的视频：https://www.bilibili.com/video/BV1Eb41177d1

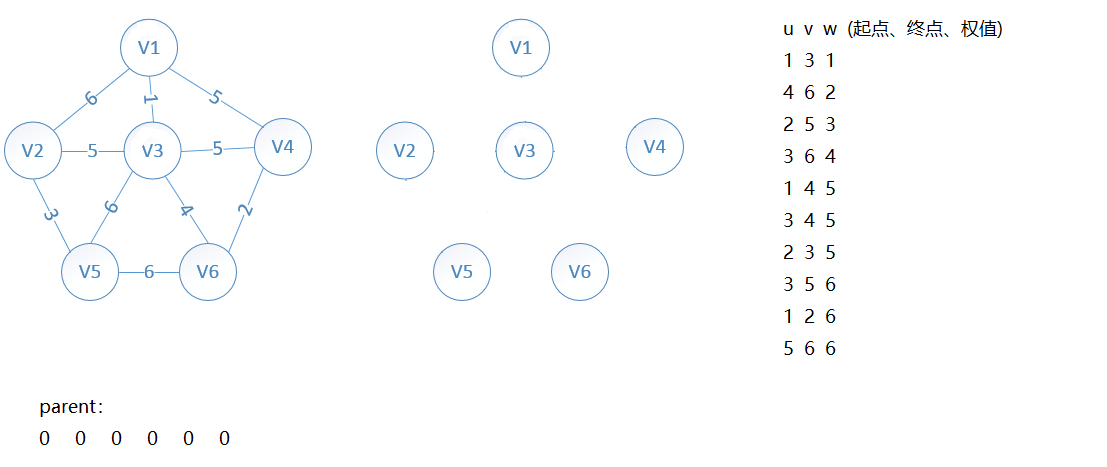
下图为初始图、只含有点的森林和点与点之间的联系

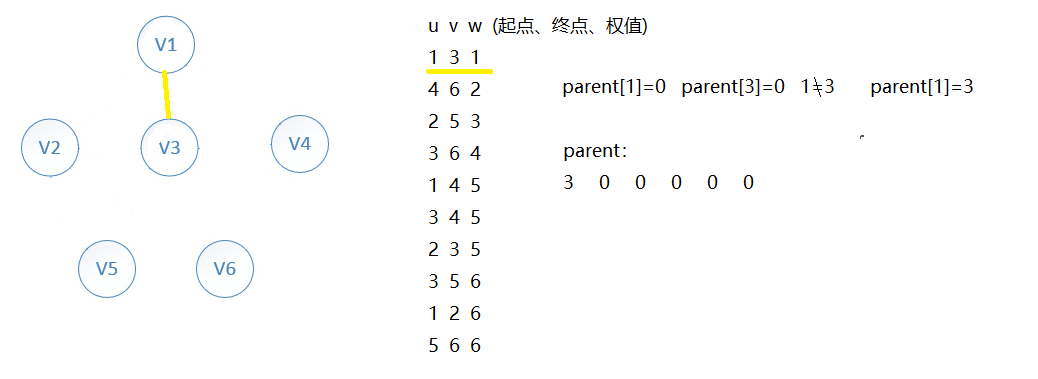
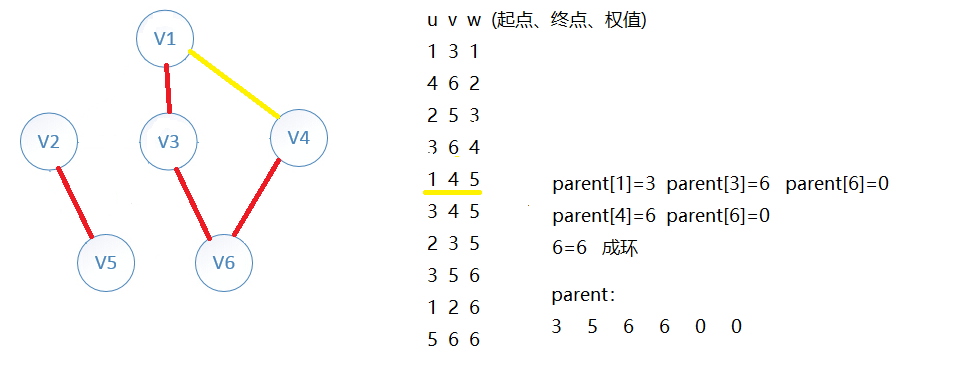
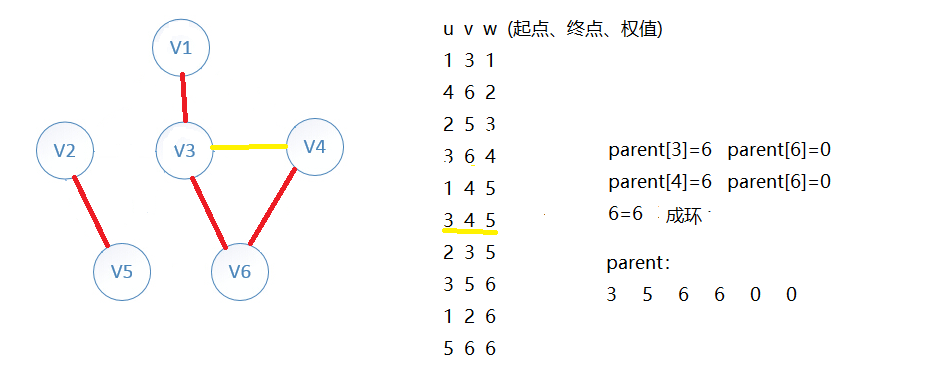
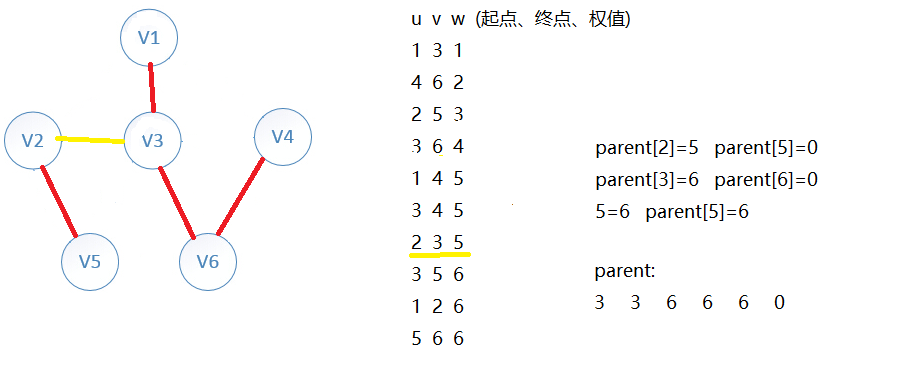
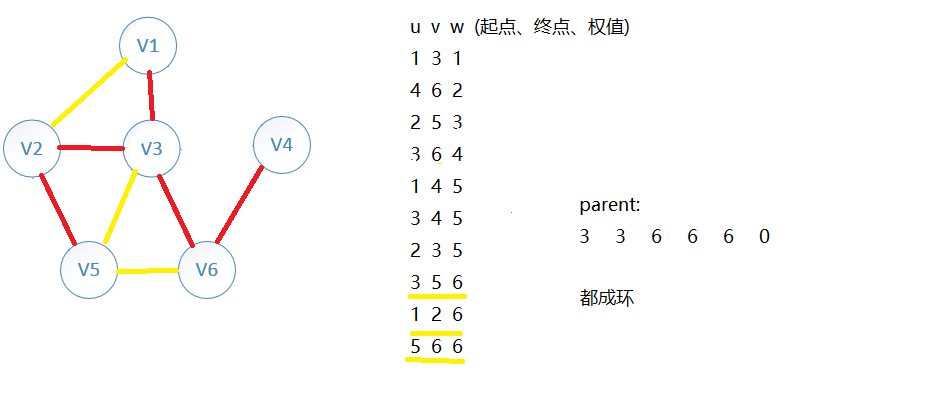
循环找权值最小的边

 

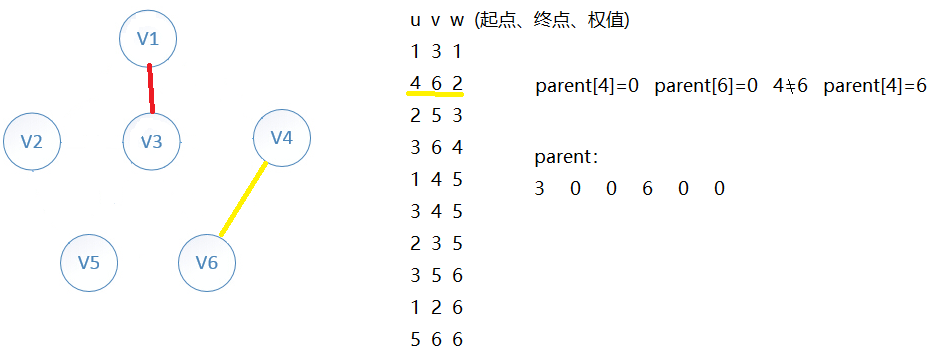
 依次向下循环...

  

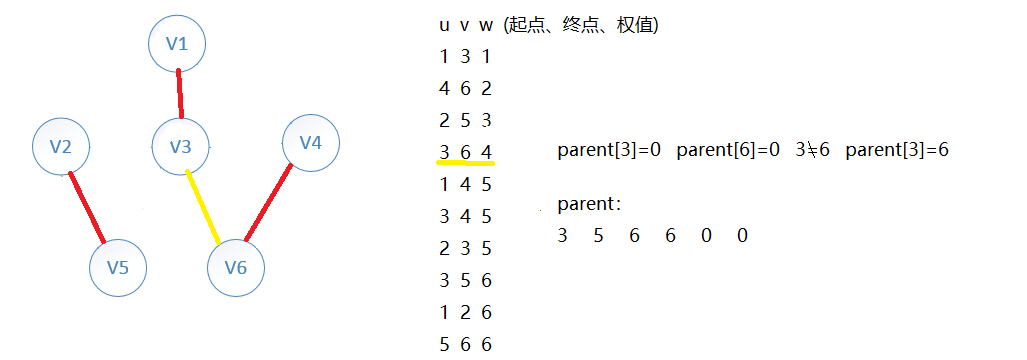
输入：

6 10
1 2 6
1 3 1
1 4 5
2 3 5
2 5 3
3 4 5
3 5 6
3 6 4
4 6 2
5 6 6

输出：

V1-V3=1
V4-V6=2
V2-V5=3
V3-V6=4
V5-V6=5
15

代码：

#include <iostream>
#include <bits/stdc++.h>
using namespace std;

#define MAX 100

int Find(int parent[],int i)
{
    while(parent[i]>0)
    {
        i=parent[i];
    }
    return i;
}
void Kruskal(int u[],int v[],int w[],int n,int m)
{
    int parent[MAX];
    int sum=0;
    for(int i=1;i<=n;i++) //初始化
    {
        parent[i]=0;
    }
    int a,b;
    for(int i=1;i<=m;i++)
    {
        a=Find(parent,u[i]);
        b=Find(parent,v[i]);
        if(a!=b) //a==b说明成环
        {
            parent[a]=b;
            cout<<"V"<<a<<"-"<<"V"<<b<<"="<<w[i]<<endl;
            sum+=w[i];
        }
    }
    cout<<sum;
}
int main()
{
    int n,m;
    int u[MAX],v[MAX],w[MAX];
    cin>>n>>m;
    for(int i=1;i<=m;i++)
    {
        cin>>u[i]>>v[i]>>w[i];
    }
    for(int i=1;i<=m;i++)  //排序
    {
        int min=i;
        for(int j=i+1;j<=m;j++)
        {
            if(w[min]>w[j])
            {
                min=j;
            }
        }
        swap(u[i],u[min]);
        swap(v[i],v[min]);
        swap(w[i],w[min]);
    }
    Kruskal(u,v,w,n,m);
    return 0;
}