题意：给定n(n≤106)个数，要求将它化为混偱环小数的形式，即前k个数不参与循环，之后所有数以p为循环节长度进行循环。求k和p，要求k+p尽量小，k+p相等时要求p尽量小。
样例1
输入：
6
612534 3157 423 3157 423 3157
输出：
1 2
样例2
输入：
9
1 2 1 3 1 2 1 3 1
输出：
0 4
分析：想了两个晚上，没有想到有什么数据结构可以支持这种操作，想要二分答案又不满足单调性，于是去请教TJW，TJW一语点醒梦中人：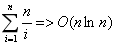
（还是log n的？，不大清楚）。那么直接暴力枚举p，然后均摊O(ln n)验证一下即可。以上是TJW的原话，具体细节还要处理一下：比如如何O(1)比对两段数？哈希即可，具体写法是设一个base数组，base[i]表示哈希常数key的i次方，再开一个hash数组，hash[i]表示前i位的哈希值，具体构造方法是，hash[i]=hash[i-1]*key。然后求l-r的hash值时只要求hash[r]-hash[l-1]*base[r-l+1]。除此以外，还有一个问题：循环节的开头（结尾）不一定是完整的，如何用较小的复杂度计算这段不完整的开头的长度？如果直接一个一个判断，整体复杂度就退化为O(n^2)了。这里我的解决方法是二分（刚好满足单调性），整体复杂度大概是O(nlogn + nlnn)。
1 /* Gym 101667I Slot Machines 2 1st Edition:2018.1.13 Saturday 3 Algorithm:Simulation 4 */ 5 #include <iostream> 6 #include <cstdio> 7 #include <algorithm> 8 #include <cmath> 9 #include <cstring> 10 #include <vector> 11 #include <map> 12 #include <set> 13 #include <bitset> 14 #include <queue> 15 #include <deque> 16 #include <stack> 17 #include <iomanip> 18 #include <cstdlib> 19 #include <ctime> 20 #include <cctype> 21 using namespace std; 22 23 #define is_lower(c) (c>='a' && c<='z') 24 #define is_upper(c) (c>='A' && c<='Z') 25 #define is_alpha(c) (is_lower(c) || is_upper(c)) 26 #define is_digit(c) (c>='0' && c<='9') 27 #define stop system("PAUSE") 28 #define ForG(a,b,c) for(int (a)=c.head[b];(a);(a)=c.E[a].nxt) 29 #define For(a,b,c) for(int (a)=(b);(a)<=(c);++a) 30 #define min(a,b) ((a)<(b)?(a):(b)) 31 #define max(a,b) ((a)>(b)?(a):(b)) 32 #define shl(x,y) ((x)<<(y)) 33 #define shr(x,y) ((x)>>(y)) 34 #define mp make_pair 35 #define pb push_back 36 #ifdef ONLINE_JUDGE 37 #define hash rename_hash 38 #define next rename_next 39 #define prev rename_prev 40 #endif 41 typedef long long ll; 42 typedef unsigned long long ull; 43 typedef pair<int,int> pii; 44 typedef pair<ll,ll> pll; 45 typedef vector<int> vi; 46 typedef double db; 47 const ll inf=2000000007LL; 48 const double EPS=1e-10; 49 const ll inf_ll=(ll)1e18; 50 const ll maxn=1000005LL; 51 const ll mod=1000000007LL; 52 53 int n; 54 int a[maxn]; 55 56 ull base[maxn]; 57 ull hash[maxn]; 58 const ll hash_base=11; 59 60 inline ull get_hash(int l,int r){ 61 return (hash[r]-hash[l-1]*base[r-l+1]); 62 } 63 64 int main(){ 65 scanf("%d",&n); 66 base[0]=1; 67 For(i,1,n) base[i]=base[i-1]*hash_base; 68 For(i,1,n){ 69 scanf("%d",a+i); 70 hash[i]=hash[i-1]*hash_base+a[i]; 71 } 72 /* 73 For(i,1,n) printf("%llu ",hash[i]); 74 puts(""); 75 */ 76 int ansk=inf>>1,ansp=inf>>1; 77 For(i,1,n){ 78 int pos=n; 79 ull nhash=get_hash(n-i+1,n); 80 while(pos-i>=0){ 81 if(get_hash(pos-i+1,pos)!=nhash) break; 82 pos-=i; 83 } 84 int l=1,r=i+1,mid,res=0; 85 while(l<r){ 86 mid=(l+r)>>1; 87 if(pos-mid+1<=0 || get_hash(pos-mid+1,pos)!=get_hash(n-mid+1,n)) r=mid; 88 else{l=mid+1;res=mid;} 89 } 90 pos-=res; 91 if(i+pos<ansk+ansp){ 92 ansk=pos; 93 ansp=i; 94 } 95 // printf("%d %d ",pos,i); 96 } 97 printf("%d %d ",ansk,ansp); 98 return 0; 99 } 100 101 /* 102 6 103 1 2 3 4 3 4 104 105 6 106 1 2 3 4 5 6 107 108 6 109 1 2 3 4 1 29 110 111 6 112 612534 3157 423 3157 423 3157 113 114 9 115 1 2 1 3 1 2 1 3 1 116 117 */
UPD.调和级数O(ln n) QwQ