题目背景
滚粗了的HansBug在收拾旧数学书,然而他发现了什么奇妙的东西。
题目描述
蒟蒻HansBug在一本数学书里面发现了一个神奇的数列,包含N个实数。他想算算这个数列的平均数和方差。
输入输出格式
输入格式:第一行包含两个正整数N、M,分别表示数列中实数的个数和操作的个数。
第二行包含N个实数,其中第i个实数表示数列的第i项。
接下来M行,每行为一条操作,格式为以下两种之一:
操作1:1 x y k ,表示将第x到第y项每项加上k,k为一实数。
操作2:2 x y ,表示求出第x到第y项这一子数列的平均数。
操作3:3 x y ,表示求出第x到第y项这一子数列的方差。
输出格式:输出包含若干行,每行为一个实数,即依次为每一次操作2或操作3所得的结果(所有结果四舍五入保留4位小数)。
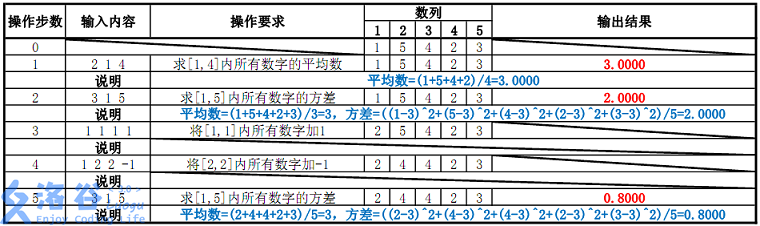
输入输出样例
说明

样例说明:
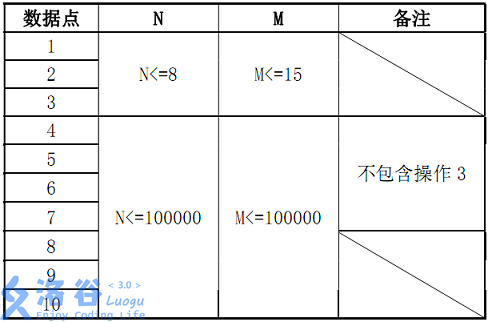
数据规模:
分析:一道线段树裸题,公式做稍微的变形就行了。拿到一道线段树的题首先要想的是用什么信息可以维护题目要求的东西?
对于这道题是方差(和平均值,平均值就跳过了吧。。),容易想到要维护区间和sum与区间平方和sumsqr。设区间长度为len,则此时有s=-(sum/len)2+sumsqr/len。这样就能维护方差了。
第二步是考虑修改时如何维护这两个信息。sum不用说,但是sumsqr怎么办呢?依然是公式的变形:
设区间加的值为add,修改后的sumsqr值为sumsqr‘,则此时有sumsqr'=sumsqr+add2*len+2*add*sum。注意这里的sum是修改前的sum,因此要先修改sumsqr再修改sum。
处理好这些细节,还有一个注意点,就是s的计算公式中出现了(sum/len)2这种东西,我一开始写的时候是sum*sum/(len*len),结果连double都炸了,因此应该先除后乘(sum/len)*(sum/len)。