【模板】FFT

FFT（快速傅里叶变换）

前置知识

• 首先要了解复数，三角函数

• FFT主要是将系数表达式转换为点值表达式，相乘后再转为系数表达式（因为点值表达式可以(O(n))相乘）。然而这样转换的复杂度又是(O(n^2))的，所以考虑优化转换。

  • 单位根定义：在复平面上(n)（(n)为2的正整数次幂）等分一个单位圆的点。不妨设(n=8)，如图所示

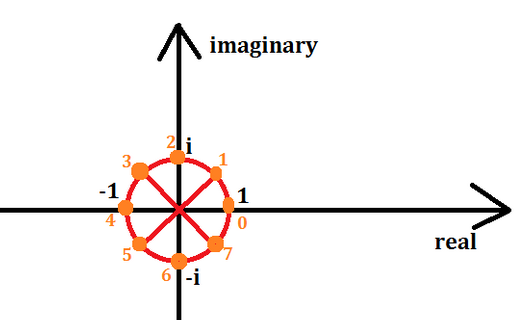
    其中(0sim7)就是单位根。其中编号为(k)的点表示的复数记作(w_n^k)。

  • 单位根性质：

    • ((w_n^1)^k=w_n^k) 显然可以用复数运算推导出
    • (w_n^k=cosfrac{k}{n}2pi+icdotsinfrac{k}{n}2pi) 同样显然
    • (w_{2n}^{2k}=w_{n}^k) 证明：(w_{2n}^{2k}=cosfrac{2k}{2n}2pi+icdotsinfrac{2k}{2n}2pi=cosfrac{k}{n}2pi+icdotsinfrac{k}{n}2pi=w_n^k)
    • (w_n^{k+frac{n}{2}}=-w_n^k) 证明：(w_n^{k+frac{n}{2}}=w_n^kcdot w_n^{frac{n}{2}}=w_n^kcdot(cospi+icdotsinpi)=-w_n^k)
    • (w_n^0=w_n^n) 显然

FFT的递归实现

DFT

考虑快速将系数表达式转换为点值表达式

设多项式(A(X)=sumlimits_0^na_ix^i=a_0+a_1x+a_2x^2+cdots+a_nx^n)设(n)为奇数

将其按(x)次数的奇偶分类，得到(A(x)=(a_0+a_2x^2+cdots+a_{n-1}x^{n-1})+x(a_1+a_3x^2+cdots+a_{n}x^{n-1}))

设(A1(x)=a_0+a_2x+a_4x^2+cdots+a_{n-1}x^{frac{n-1}{2}})，(A2(x)=a_1+a_3x+a_5x^2+cdots+a_nx^{frac{n-1}{2}})

可知(A(x)=A1(x^2)+xA2(x^2))

再设(k<frac{n}{2})，将(w_n^k) 和(w_n^{k+frac{n}{2}}) 分别代入(A(x)) 中

得

(A(w_n^k)=A1((w_n^k)^2)+w_n^kA2((w_n^k)^2)=A1(w_n^{2k})+w_n^kA2(w_n^{2k})=A1(w_{frac{n}{2}}^{k})+w_n^kA2(w_frac{n}{2}^k))

(A(w_n^{k+frac{n}{2}})=A1((w_n^{k+frac{n}{2}})^2)+w_n^{k+frac{n}{2}}A2((w_n^{k+frac{n}{2}})^2)=A1(w_n^{2k+n})-w_n^kA2(w_n^{2k+n})=A1(w_{frac{n}{2}}^{k})-w_n^kA2(w_frac{n}{2}^k))

发现两个式子中只有一项符号不同，于是可以分治。

IDFT

还要将乘完后的点值表达式转回系数表达式

有一个结论 （证明咕咕） ：一个多项式在分治的过程中乘上单位根的共轭复数，分治完的每一项除以n即为原多项式的每一项系数

其中共轭复数指设复数(z=a+bi)，则(z)的共轭复数为(a-bi)。

所以说可以将DFT和IDFT一起做。

代码

#include <cmath>
#include <cstdio>
const int N=4000010;
const double Pi=acos(-1.0);
int n,m,len=1;
struct Complex {
	double x,y;
	Complex(double xx=0,double yy=0) { x=xx; y=yy; }
}a[N],b[N];
Complex operator +(Complex x,Complex y) { return Complex(x.x+y.x,x.y+y.y); }
Complex operator -(Complex x,Complex y) { return Complex(x.x-y.x,x.y-y.y); }
Complex operator *(Complex x,Complex y) { return Complex(x.x*y.x-x.y*y.y,x.x*y.y+x.y*y.x); }
void FFT(Complex *x,const int& len,const int& type) {
	if (len==1) return;
	Complex x1[len>>1],x2[len>>1];
	for (register int i=0;i<len;i+=2) {
		x1[i>>1]=x[i]; x2[i>>1]=x[i+1];
	}
	FFT(x1,len>>1,type); FFT(x2,len>>1,type);
	Complex UR=Complex(cos(2.0*Pi/len),type*sin(2.0*Pi/len)),w=Complex(1,0);
	for (register int i=0,_n=len>>1;i<_n;++i,w=w*UR) {
		x[i]=x1[i]+x2[i]*w;
		x[i+_n]=x1[i]-x2[i]*w;
	}
}
int main() {
	scanf("%d%d",&n,&m);
	for (register int i=0;i<=n;++i) scanf("%lf",&a[i].x);
	for (register int i=0;i<=m;++i) scanf("%lf",&b[i].x);
	n+=m; for (;len<=n;len<<=1);
	FFT(a,len,1); FFT(b,len,1);
	for (register int i=0;i<=len;++i) a[i]=a[i]*b[i];
	FFT(a,len,-1);
	for (register int i=0;i<=n;++i) printf("%d%c",(int)(a[i].x/len+0.5)," 
"[i==n]);
}

FFT的迭代实现

由于递归版本常数较大，考虑优化。递归过程如下图：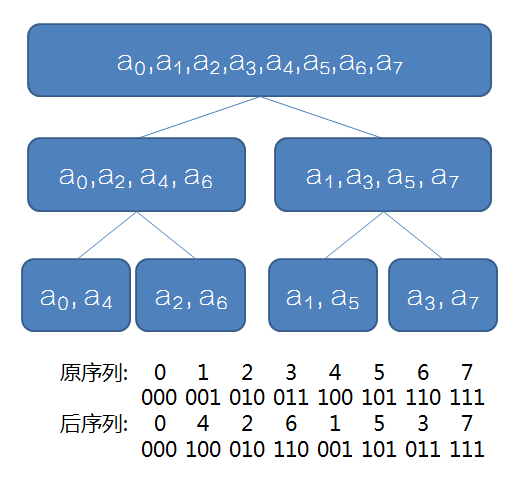

容易发现每个位置分治后的最终位置为其二进制翻转后得到的位置。

所以我们可以预先将原序列变换好，就可以迭代实现了。

代码

#include <cmath>
#include <cctype>
#include <cstdio>
#include <algorithm>
const int N=4000010;
const double Pi=acos(-1.0);
int n,m,lim=1,l=-1,r[N];
struct Complex {
	double x,y;
	Complex(double xx=0,double yy=0) { x=xx; y=yy; }
}a[N],b[N];
Complex operator +(Complex x,Complex y) { return Complex(x.x+y.x,x.y+y.y); }
Complex operator -(Complex x,Complex y) { return Complex(x.x-y.x,x.y-y.y); }
Complex operator *(Complex x,Complex y) { return Complex(x.x*y.x-x.y*y.y,x.x*y.y+x.y*y.x); }
inline void FFT(Complex *x,const int& lim,const int& type) {
	for (register int i=0;i<lim;++i) if (i<r[i]) std::swap(x[i],x[r[i]]);
	for (register int i=1;i<lim;i<<=1) {
		Complex UR(cos(Pi/i),sin(Pi/i)*type);
		for (register int j=0,I=i<<1;j<lim;j+=I) {
			Complex w(1,0);
			for (register int k=0;k<i;++k,w=w*UR) {
				Complex t1=x[j+k],t2=w*x[k+i+j];
				x[j+k]=t1+t2; x[j+k+i]=t1-t2;
			}
		}
	}
}
int main() {
	scanf("%d%d",&n,&m);
	for (register int i=0;i<=n;++i) scanf("%lf",&a[i].x);
	for (register int i=0;i<=m;++i) scanf("%lf",&b[i].x);
	n+=m; for (;lim<=n;lim<<=1,++l);
	for (register int i=0;i<lim;++i) r[i]=(r[i>>1]>>1)|((i&1)<<l);
	FFT(a,lim,1); FFT(b,lim,1);
	for (register int i=0;i<lim;++i) a[i]=a[i]*b[i];
	FFT(a,lim,-1);
	for (register int i=0;i<=n;++i) printf("%d%c",(int)(a[i].x/lim+0.5)," 
"[i==n]);
}

三次变两次优化

注意到我们要做两次DFT才能将2个系数表达式变为点值表达式，这是可以优化的。

若求(A*B)

设(C=A+iB) 则(C^2=A^2-B^2+i2AB) 发现(C)的虚部正是答案的两倍。

所以只做一次DFT就可变为点值表达式，常数减小(frac{1}{3})，跑的和NTT差不多。

注意：这个优化会损失精度，再加上FFT中小数乘法损失的精度，可能会爆精度

代码

#include <cmath>
#include <cctype>
#include <cstdio>
#include <algorithm>
const int N=4000010;
const double Pi=acos(-1.0);
int n,m,lim=1,l=-1,r[N];
struct Complex {
	double x,y;
	Complex(double xx=0,double yy=0) { x=xx; y=yy; }
}a[N];
Complex operator +(Complex x,Complex y) { return Complex(x.x+y.x,x.y+y.y); }
Complex operator -(Complex x,Complex y) { return Complex(x.x-y.x,x.y-y.y); }
Complex operator *(Complex x,Complex y) { return Complex(x.x*y.x-x.y*y.y,x.x*y.y+x.y*y.x); }
inline void FFT(Complex *x,const int& lim,const int& type) {
	for (register int i=0;i<lim;++i) if (i<r[i]) std::swap(x[i],x[r[i]]);
	for (register int i=1;i<lim;i<<=1) {
		Complex UR(cos(Pi/i),sin(Pi/i)*type);
		for (register int j=0,I=i<<1;j<lim;j+=I) {
			Complex w(1,0);
			for (register int k=0;k<i;++k,w=w*UR) {
				Complex t1=x[j+k],t2=w*x[k+i+j];
				x[j+k]=t1+t2; x[j+k+i]=t1-t2;
			}
		}
	}
}
int main() {
	scanf("%d%d",&n,&m);
	for (register int i=0;i<=n;++i) scanf("%lf",&a[i].x);
	for (register int i=0;i<=m;++i) scanf("%lf",&a[i].y);
	n+=m; for (;lim<=n;lim<<=1,++l);
	for (register int i=0;i<lim;++i) r[i]=(r[i>>1]>>1)|((i&1)<<l);
	FFT(a,lim,1);
	for (register int i=0;i<lim;++i) a[i]=a[i]*a[i];
	FFT(a,lim,-1);
	for (register int i=0;i<=n;++i) printf("%d%c",(int)(a[i].y/lim/2+0.5)," 
"[i==n]);
}