(邻接矩阵)最短路径算法

 

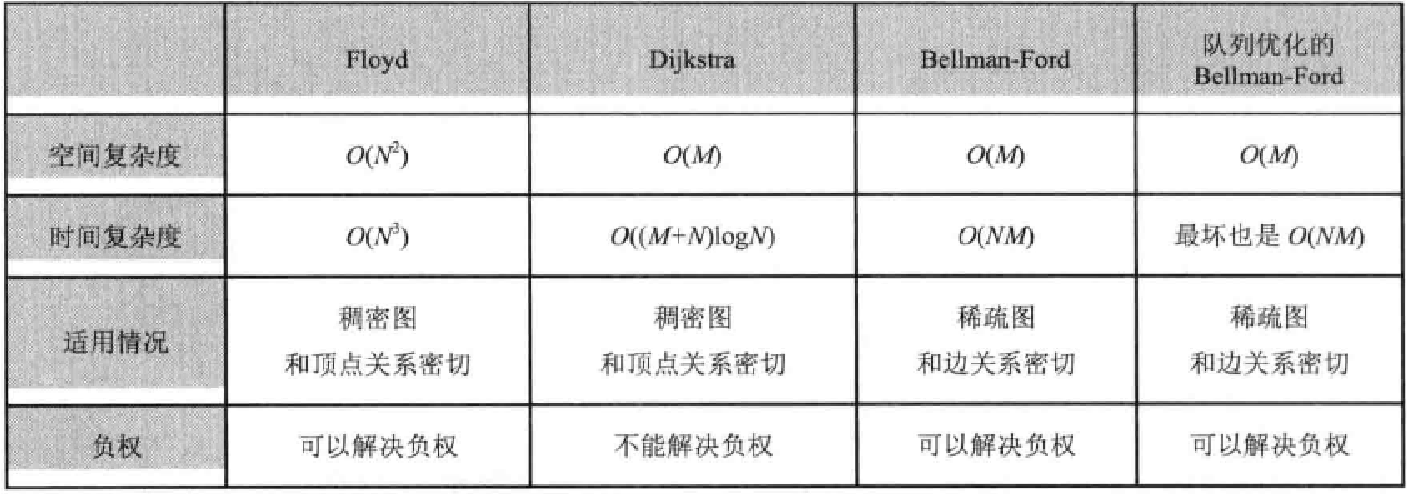
Floyd算法:

思路 ：遍历计算 i 点 经过 k 点 到 j 点 的最小路径值 (动态规划思路)

缺点：时间复杂度高，不能解决负边情况

输入样例：

4 8
1 2 2
1 3 6
1 4 4
2 3 3
3 1 7
3 4 1
4 1 5
4 3 12

输出样例：

1-->2:2
1-->3:5
1-->4:4
2-->1:9
2-->3:3
2-->4:4
3-->1:6
3-->2:8
3-->4:1
4-->1:5
4-->2:7
4-->3:10

#include <cstdio>
#include <string.h>
#include <iostream>
#include <algorithm>
#include <sstream>
#include <math.h>
#include <queue>
using namespace std;
const int inf=0x7fffff;
const long long mod=1e9+7;
const double PI=acos(-1);

int n,m,start,end;
int ans=9999999;
bool vis[105];
int e[105][105];

void init(){                           //初始化邻接矩阵 
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            if(i==j) e[i][j]=0;
            else e[i][j]=inf;
        }
    }
} 

void Floyd(){                                       //思路：依此判断 i 通过 k 到 j 的最短路 
    for(int k=1;k<=n;k++){                          // k 经转的节点 
        for(int i=1;i<=n;i++){                      // i 每次的起点 
            for(int j=1;j<=n;j++){                  // j 每次的终点 
                if(k==i&&k==j) continue;
                if(e[i][j]>e[i][k]+e[k][j]){
                    e[i][j]=e[i][k]+e[k][j];
                }
            }
        }
    }
}

int main()
{
    int x,y,value;
    cin>>n>>m;
    init();
    for(int i=0;i<m;i++){
        cin>>x>>y>>value;
        e[x][y]=value;
    }
    Floyd();
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            if(i==j) continue;
            cout<<i<<"-->"<<j<<":"<<e[i][j]<<endl;
        }
    } 
    return 0;
}

 Dijkstra算法：

思路：依此找起点可达的点的最小值点。通过最小值点再访问其他点。不断更新最小距离。

测试数据：

6 9 1         (6个点9条边 1为起点)
1 2 1
1 3 12
2 3 9
2 4 3
3 5 5
4 3 4
4 5 13
4 6 15
5 6 4

输出数据：

1-->1:0
1-->2:1
1-->3:8
1-->4:4
1-->5:13
1-->6:17

#include <cstdio>
#include <string.h>
#include <iostream>
#include <algorithm>
#include <sstream>
#include <math.h>
#include <queue>
using namespace std;
const int inf=0x7fffff;
const long long mod=1e9+7;
const double PI=acos(-1);

int n,m,start,end;
int ans=9999999;
bool vis[105];
int e[105][105];
void init(){                                //初始化邻接矩阵 
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            if(i==j) e[i][j]=0;
            else e[i][j]=inf;              //设 inf 为 ∞ 表示两点不通 
        }
    }
} 
void Dijkstra(int s){                        //Dijkstra算法为单源最短路径算法 s 为起点 
    int dis[n+1];                           // dis 用来 记录每次操作时 s 到每个点的最短路径 
    int minp;                              // 记录目前操作的最小距离点 
    int min=inf;                     
    
    for(int i=1;i<=n;i++){                 //初始化最短距离数组 dis 
        dis[i]=e[s][i];
    }
    vis[s]=1;                              
    for(int i=1;i<=n;i++){              
        min=inf;
        for(int j=1;j<=n;j++){              //每次找dis数组里面最小未访问过的值  
            if(min>dis[j]&&!vis[j]){
                min=dis[j];                  //min 表示此时未访问过的最小距离
                minp=j;                      //minj表示未访问过的最小距离那个点 
            } 
        }
        vis[minp]=1;                     //设置访问 
        for(int v=1;v<=n;v++){           //每次访问 此时与最小值点相连的点v 
            if(e[minp][v]<inf){          //该点可达 
                if(dis[v]>dis[minp]+e[minp][v]){   //s直接到 v 的距离大于 s通过 最小值点到 v 的距离，则更新 
                    dis[v]=dis[minp]+e[minp][v];   
                }
            }
        }
    }
    for(int i=1;i<=n;i++){
        cout<<s<<"-->"<<i<<":"<<dis[i]<<endl;   //遍历 s 到 每个点的最小距离 
    }
}
int main()
{
    int x,y,value,s;
    cin>>n>>m>>s;
    init();
    for(int i=0;i<m;i++){
        cin>>x>>y>>value;
        e[x][y]=value;
    }
    Dijkstra(s);               //s 为起点 
    return 0;
}

 Bellman_Floyd算法:

思路：经过n-1次迭代，判断每次迭代判断能不能用u[i]-->v[i]

　　   使源点到v[i]的最短路径变短。

优点：可以解决带负边的问题。

输入样例：

5 5 1 （5个点 5条边 起点1）
2 3 2
1 2 -3
1 5 5
4 5 2
3 4 3

输出样例：

0 -3 -1 2 4 （起点到各个点的最短路径）

#include <cstdio>
#include <string.h>
#include <iostream>
#include <algorithm>
#include <sstream>
#include <math.h>
#include <vector>
using namespace std;
const int inf=999999;//0x7fffff
const long long mod=1e9+7;
const double PI=acos(-1);

int n,m;
int ans=9999999;
bool vis[105];
int dis[105],u[105],v[105],w[105];
void Bellman_Floyd(int s){
    memset(dis,inf,sizeof(dis));                          //初始 dis最短路径数组 为无穷 
    dis[s]=0;
    for(int k=1;k<=n-1;k++){                              //迭代 n-1次 更新最短路径表dis 
        for(int j=1;j<=m;j++){
            dis[v[j]]=min(dis[v[j]],dis[u[j]]+w[j]);      //每次计算能不能由 u[i]到 v[i] 能不能使结果变小并更新 
        }
    }
//    bool ok=0;
//    for(int k=1;k<=m;k++){
//        if(dis[v[k]]>dis[u[k]]+w[k]) ok=1;               //检测负权回路 
//    }
}
int main()
{
    int x,y,s;
    cin>>n>>m>>s;
    for(int i=1;i<=m;i++){
        cin>>u[i]>>v[i]>>w[i];                           //u[i]边起使点 v[i]边指向点 w[i] 权值 
    }
    Bellman_Floyd(s);
    for(int i=1;i<=n;i++){
        cout<<dis[i]<<" ";
    }
    return 0;
}