POJ1247-Magnificent Meatballs

http://poj.org/problem?id=1247

Magnificent Meatballs

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 6739		Accepted: 4471

Description

Sam and Ella run a catering service. They like to put on a show when serving meatballs to guests seated at round tables. They march out of the kitchen with pots of meatballs and start serving adjacent guests. Ella goes counterclockwise and Sam goes clockwise, until they both plop down their last meatball, at the same time, again at adjacent guests. This impressive routine can only be accomplished if they can divide the table into two sections, each having the same number of meatballs. You are to write a program to assist them. 

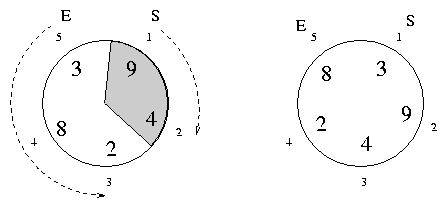
At these catering events, each table seats 2 <= N <= 30 guests. Each guest orders at least one and at most nine meatballs. Each place at the table is numbered from 1 to N, with the host at position 1 and the host's spouse at position N. Sam always serves the host first then proceeds to serve guests in increasing order. Ella serves the spouse first, then serves guests in decreasing order. The figures illustrate the first two example input cases. 

Input

Input consists of one or more test cases. Each test case contains the number of guests N followed by meatballs ordered by each guest, from guest 1 to guest N. The end of the input is a line with a single zero. 

Output

For each table, output a single line with the ending positions for Sam and Ella, or the sentence indicating an equal partitioning isn't possible. Use the exact formatting shown below. 

Sample Input

5 9 4 2 8 3
5 3 9 4 2 8
6 1 2 1 2 1 2
6 1 2 1 2 1 1
0

Sample Output

Sam stops at position 2 and Ella stops at position 3.
No equal partitioning.
No equal partitioning.
Sam stops at position 3 and Ella stops at position 4.

　　其实刚开始对题目的意思没有把握准，但是把题目的意思理解了之后就非常的简单，这道题的意思可以简单的理解为：圆桌上有N个数字，Sam从1的位置开始往N走，而Ella则从N往1走，问他们哪个相遇的位置能让两端的数字的和相等；如果不论在哪个位置都不能相等的话，那就输出 No equal partitioning.

　　好了，现在就简单多了吧。

#include "stdio.h"
#include "math.h"
#include "string.h"
#include "stdlib.h"

int main(int argc, char const *argv[])
{
    int data[35], _i, n, sum, s1, s2;

    while(scanf("%d", &n), n){
        sum = 0;
        for(_i=0; _i<n; _i++){
            scanf("%d", &data[_i]);
            sum += data[_i];
        }
        s1 = 0, s2 = sum;
        for(_i=0; _i<n; _i++){
            s1 += data[_i];
            s2 -= data[_i];
            if(s1 == s2){
                break;
            }
        }
        if(_i>=n){
            printf("No equal partitioning.
");
        }else{
            printf("Sam stops at position %d and Ella stops at position %d.
", _i+1, _i+2);
        }
    }

    return 0;
}