1.数据拟合
用途:反应数据变化规律,解释数据;根据数据做出预测、判断,给决策者提供重要的依据
需要解决的问题:
1、选择什么类型的函数Φ()作为拟合函数(也即数学模型)
2、对于选定的拟合函数,如何确定拟合函数中的参数
常见的拟合函数:线性函数、多项式函数、指数函数、三角函数
模型介绍:
1、线性拟合(线性模型)
函数:y=a+bx
差异(残差):|a+bx-y|
总误差:![]()
为操作方便,常常求a, b使得函数![]() 达到最小。
达到最小。
为求得函数的极小值,令![]() ,得
,得![]()
求解该二元线性方程组便可得待定系数a,b。
2、二次函数拟合(二次多项式模型)
函数:y=a0+a1x+a2x2
求a0,a1,a2使得![]() 达到最小值。
达到最小值。
得到

3、n次多项式拟合
同二次多项式。
2.参数估计
参数估计的常见方法:图解法,统计法,机理分析法
1、图解法
精度不高,仅限于对参数做出粗略估计
2、统计法
参数估计的统计处理,往往采用最小二乘法
3、机理分析法
原理:利用经典的数学工具分析现象的因果关系
常见的经典数学工具:人口模型(增长速率先上升后下降);相变(物理概念,用于模型上某些指标的突变);博弈论(囚徒困境);微分方程(人口模型及其特例);网络传播(扩散现象)
(1)人口模型:
马尔萨斯提出人口指数增长模型,基本假设为:人口(相对)增长率r是常数。x(t)为时刻t时的人口,Δt为时间的增加量,
则有:![]() ,
,![]() ,
,![]() ,
,![]()
一个国家的人口不可能无限增长,种种因素会对人口增长产生阻滞作用,且阻滞作用随人口数量增加而变大,因此增长率r是人口数量x的减函数。记,xm为最大人口容量,可得阻滞增长模型,

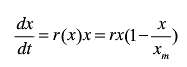 ,解得
,解得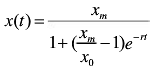
x(t)的图形如下:

(2)相变:
没有查到相关信息,希望了解的同学补充~
(3)博弈论:
定义:一些个人,对组或其他组织,面对一定的环境条件,在一定的规则下,同时或者先后,一次或者多次,从各自允许选择的行为或者策略中进行选择并加以实施,各自取得相应结果的过程。
分类:
<1>根据参与人的多少:两人博弈,多人博弈
<2>根据参与人是否合作:合作博弈,非合作博弈
合作博弈:强调团队理性
非合作博弈:强调个人理性,个人最优决策。其结果可能是有效率的也可能是无效率的。
<3>根据博弈结果的不同:零和博弈,常和博弈,变和博弈
<4>根据行动的先后次序:静态博弈,动态博弈
静态博弈指在博弈中,参与人同时选择行动,或虽然非同时但是后行动者并不知道前行动者采取了什么具体行动。
动态博弈指的是参与人的行动有先后顺序,且后行动者能够观察到先行动者所选择的动作的博弈。
<5>根据参与人对其他参与人的各种特征信息的获得差异:完全信息博弈,不完全信息博弈
完全信息博弈指的是每一个参与人对所有其他参与人的特征,如策略集合及得益函数都有准确完备的知识,否则就是不完全信息。
案例:
<1>囚徒困境:

<2>Boxed Pigs

<3>Battle of the Sexes
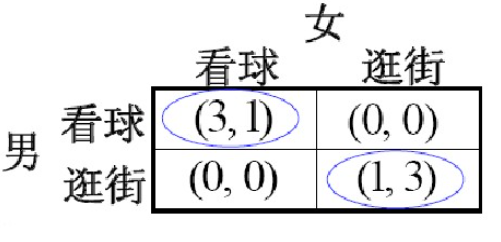
<4>Nash均衡(Hotelling问题)
两家快餐店开在同一地点,平分所有客源
但是,三方竞争是不稳定的,Nash均衡不存在。
<5>双寡头垄断


------>联合不如欺骗
<6>稳定婚姻问题


衍生问题:申请式学校录取;用人单位和求职者的双向选择;
基本要素:
<1>局中人:博弈中选择行动以最大化自己效用的决策主体(可以是个人,也可以是团体)
<2>得益:参与人在博弈结束后从博弈中获得的效用,一般是所有参与人的策略或行动的函数
<3>信息:参与人在博弈中知道的关于自己以及其他参与人的行动,策略机器得益函数等知识
<4>策略:参与人选择行动的规则,即在博弈进程中,什么情况下选择什么行动的预先安排。
<5>均衡:所有参与人的最优策略或行动的组合。
<6>行动:参与人在博弈进程中轮到自己选择时所作的某个具体决策。
(4)网络传播
貌似不是基础模型,是架构在其他模型基础之上的,暂且搁置。
3.插值
定义:通过离散数据去确定某一类已知函数的参数,或者寻求某个近似函数,使所得到的近似函数与已知数据有较高的拟合精度。注意:插值问题不一定要得到近似函数的表达形式,可以仅通过插值方法找到未知点对应的值。
分类:Lagrange插值,分段线性插值,Hermite,三次样条插值
应用:Matlab