二叉树总结

1. 树的定义

2. 相关名词， 

　　a）有序树、无序树   b）孩子、双亲、兄弟

3. 因度为2的树最节省空间，并且任意树可以向二叉树转化，因此着重研究二叉树的性质

二叉树

1.基本形态

2.满二叉树与完全二叉树

满二叉树：                            完全二叉树：

 　　    1　　　　　　　　　　      　　1

　　2            3　　　　　　　   　2            3

4         5     6         7                 4          5

3.二叉树一个很重要的性质：

        

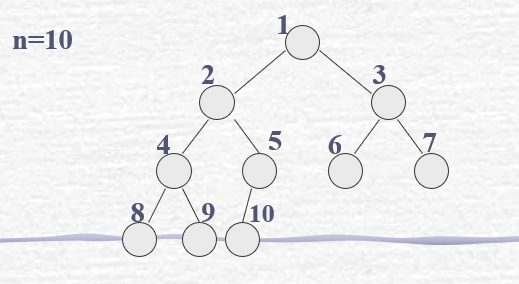
 其中，以上三条可以作为二叉树一维数组存储的实现方法。

4. 二叉树的存储方法

a） 一维数组作顺序存储，数组编号与二叉树编号相对应，该数组即为二叉树的顺序存储结构，并且某个元素的双亲或兄弟的查找方法可以通过以上3.中的三条性质确定。

　　但是，一维数组存储对于完全二叉树或满二叉树可以较好的实现，但对于一般二叉树，会浪费大量的空间。因此，衍生出第二种存储方法--链表存储。

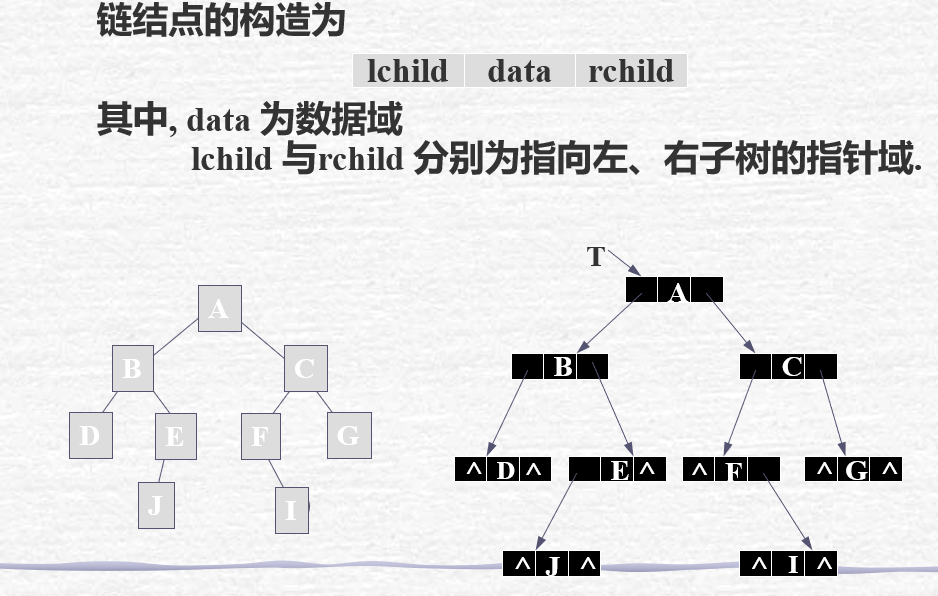
b) 二叉链表

   结构示意：

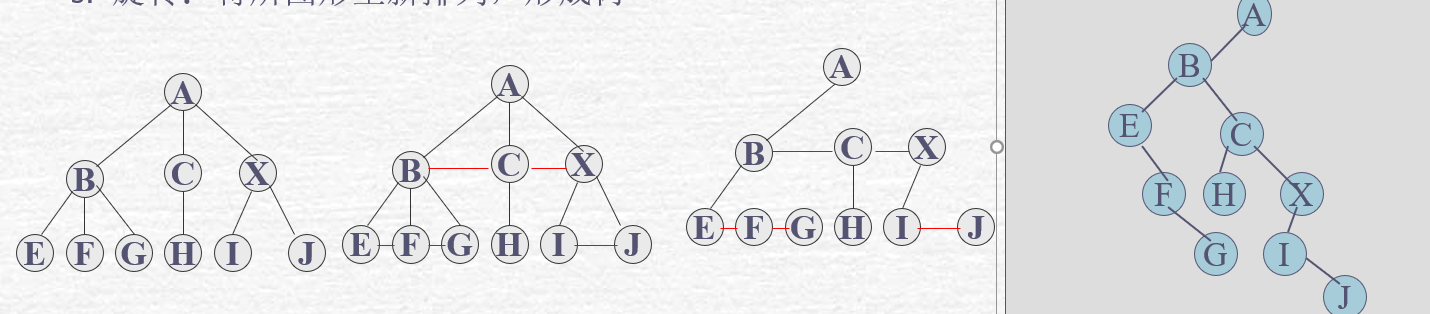
　5. 普通树向二叉树的转化方法

6. 二叉树的遍历

一、深度优先   实现方式：递归

a）前序遍历  ： 根左右  

b）中序遍历： 左根右

c）后序遍历：左右根

二、广度优先   实现方式：队列

// bintree.cpp : 定义控制台应用程序的入口点。
//

#include "stdafx.h"
#include "stdlib.h"
#define M 1024
struct node * ccbl_chudui();
void ccbl_rudui(struct node * tree);
struct node * queue[M];
int rear=-1;
int front=-1;
int flag=0;
struct node 
{
    char data;
    struct node* l;
    struct node* r;
};
struct node* Createtree(){
    char ch;
    struct node* t;
    
    scanf("%c",&ch);
    getchar();
    //fflush(stdin);
    if(ch=='#')t=NULL;
    else{
        t = ( struct node* )malloc(sizeof( struct node));
        t->data = ch;
        printf("
请输入%c结点的左结点:",t->data);
        t->l = Createtree();    
        printf("
请输入%c结点的右子结点:",t->data);
        t->r = Createtree();
    }
    return t;//返回根节点
}
int qxbl(struct node * tree)
{
    if(tree==NULL) 
        return 0;
    else
    {
        printf("%c 
",tree->data);
        qxbl(tree->l);
        qxbl(tree->r);
    }
}
int zxbl(struct node * tree)
{
        if(tree==NULL) 
        return 0;
    else
    {
    
        zxbl(tree->l);
        printf("%c 
",tree->data);
        zxbl(tree->r);
    }
}
int hxbl(struct node * tree)
{
        if(tree==NULL) 
        return 0;
    else
    {
        hxbl(tree->l);
        hxbl(tree->r);
        printf("%c 
",tree->data);
    }
}
int ccbl(struct node * tree)
{
    
    if(tree==NULL)return 0;
    printf("%c
",tree->data);
    if(tree->l!=NULL)
    ccbl_rudui(tree->l);   //记录B
    if(tree->r!=NULL)
    ccbl_rudui(tree->r);    //记录C
    tree=ccbl_chudui();
    if(front==rear)
    {  
        flag++;
        if(flag==1)
            ccbl(tree);
    return 0;}
    else
    ccbl(tree);
}

void ccbl_rudui(struct node * tree)
{
    if(rear==M-1)
        printf("
 队列已满！");
    else
    {
    rear++;
    queue[rear]=tree;
    }
}
struct node * ccbl_chudui()
{
    if(front==rear)
    {    printf("队列已空！");
    return queue[front];}
    else
    {
        front++;
        return queue[front];
    }
}

int _tmain(int argc, _TCHAR* argv[])
{    
    struct node *tree;
    printf("请输入根节点的数据值  #代表NULL 
");
    tree=Createtree();
    printf("
前序遍历:
");
    qxbl(tree);
    printf("
中序遍历:
");
    zxbl(tree);
    printf("
后序遍历:
");
    hxbl(tree);
    printf("层次遍历
");
    ccbl(tree);
    system("pause");
    return 0;
}

 三、二叉树的层次遍历（广度优先）

　　使用队列

void ccbl(struct node * root)
{
    struct node * queue[1024];
    struct node * p;
    int front, rear;
    if (root != NULL)
    {
        queue[0] = root;
        front = -1;
        rear = 0;
    }
    while (front < rear)    //队列不空
    {
        p = queue[++front];
        printf("%c", p->data); //访问p
        if (p->l != NULL)
            queue[++rear] = p->l;
        if (p->r != NULL)
            queue[++rear] = p->r;


    }
}

 四、前序遍历的非递归算法 　　使用堆栈

void fdgbl(struct node * root)
{
    struct node * p;
    p = root;
    while(p!=NULL)
    {
        printf("%c", root->data);
        
        if (root->r != NULL) push(root->r);
        if (root->l != NULL) 
                    p = p->l;
        else
        {
            if (!empty())
                p = pop();
            else
                p = NULL;
        }
                
    }
}