No.1. 线性回归算法的特点

No.2. 分类问题与回归问题的区别
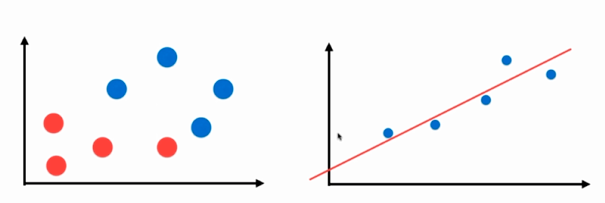
上图中,左侧为分类问题,右侧为回归问题。左侧图中,横轴和纵轴表示的都是样本的特征,用不同的颜色来作为输出标记,表示不同的种类;左侧图中,只有横轴表示的是样本特征,纵轴用来作为输出标记,这是因为回归问题所预测的是一个连续的数值,无法用离散的几种颜色来表示,它需要占据一个坐标轴的空间。在回归问题中,如果需要考虑两个样本特征,那就必须在三维空间中进行观察。
No.3. 简单线性回归与多元线性回归
样本特征只有一个的线性回归,就称之为简单线性回归;样本特征有多个的线性回归,就称之为多元线性回归。
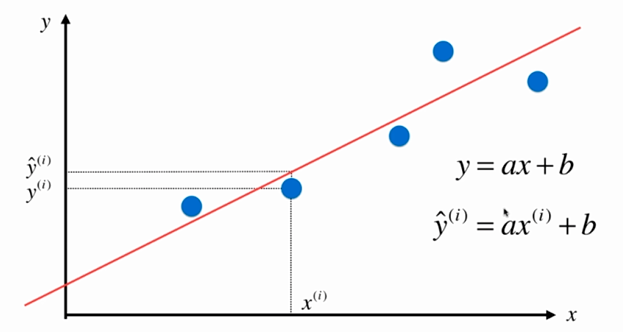
No.4. 简单线性回归就是要找一条直线,这条直线要能最大程度地拟合样本特征点,这条直线的一般性表达式为:y=ax+b,其中,a 表示直线的斜率,b 表示直线的截距。对于任意一个样本点 i ,会有一个对应的样本特征 x(i),以及一个输出标记 y(i),如果我们确定了这条直线的两个参数 a 和 b 的话,我们就可以将 x(i) 这个特征值代入到直线方程 y=ax+b中,得到特征值 x(i) 的输出标记的预测值,表示如下:

当然这个输出标记的预测值与真实值之间存在一定的差距,我们需要想办法使这个差距尽可能小。
No.5. 求解简单线性回归的过程大致如下:

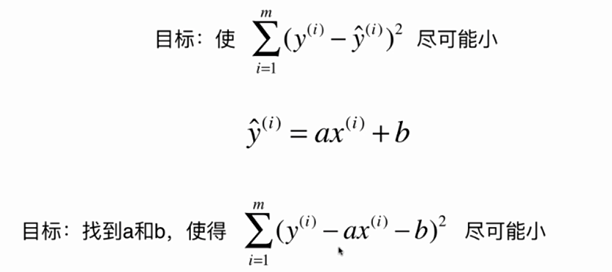

No.6. 最小二乘法的"套路"
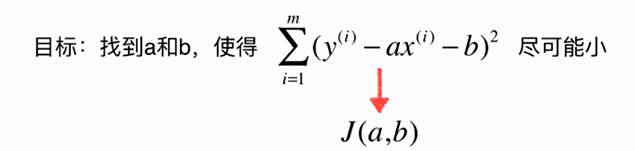
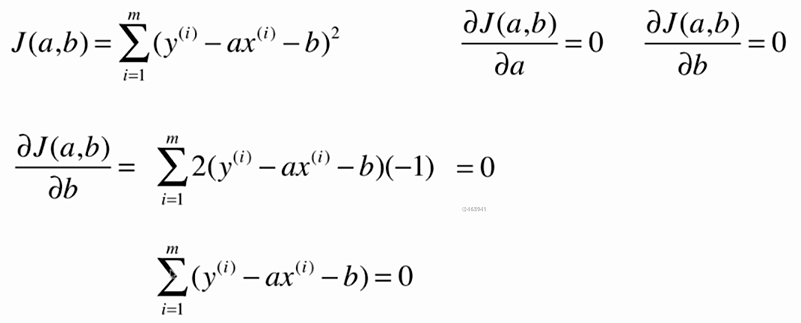
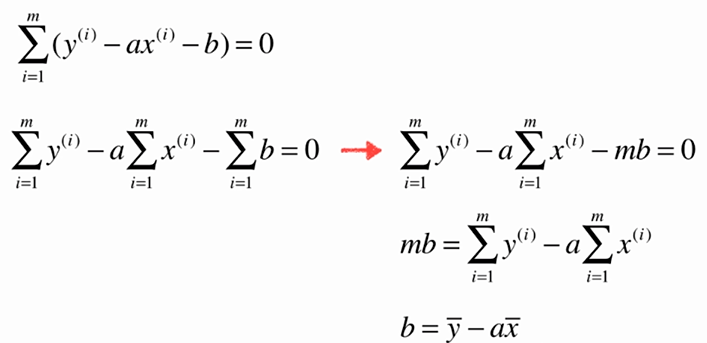
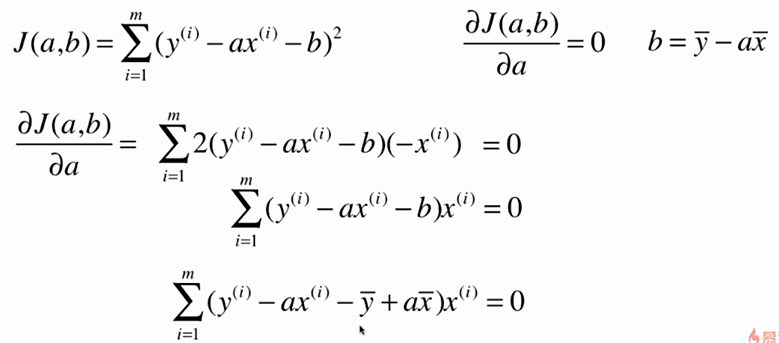

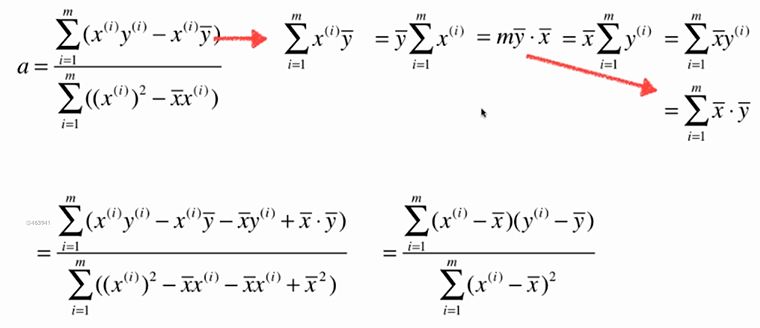
No.7. 实现一个简单线性规划
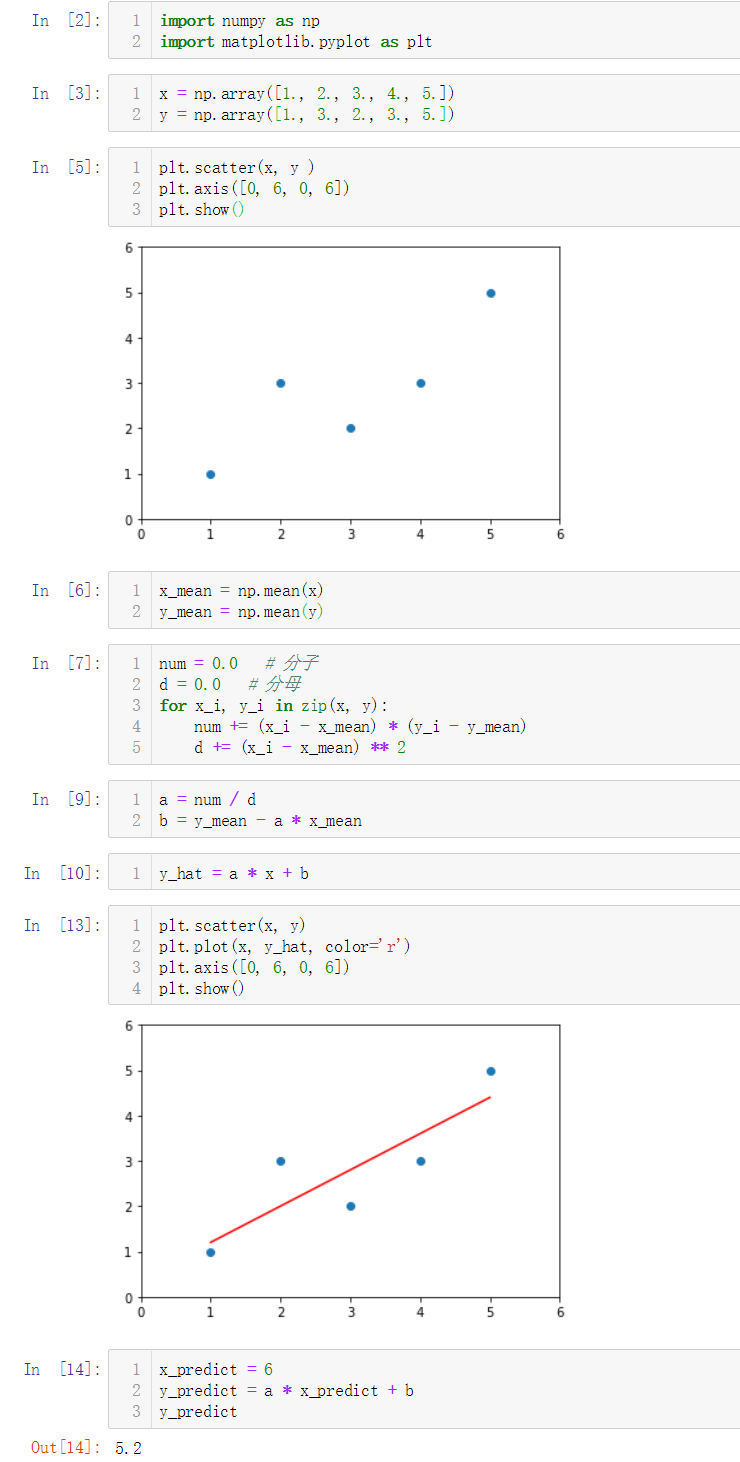
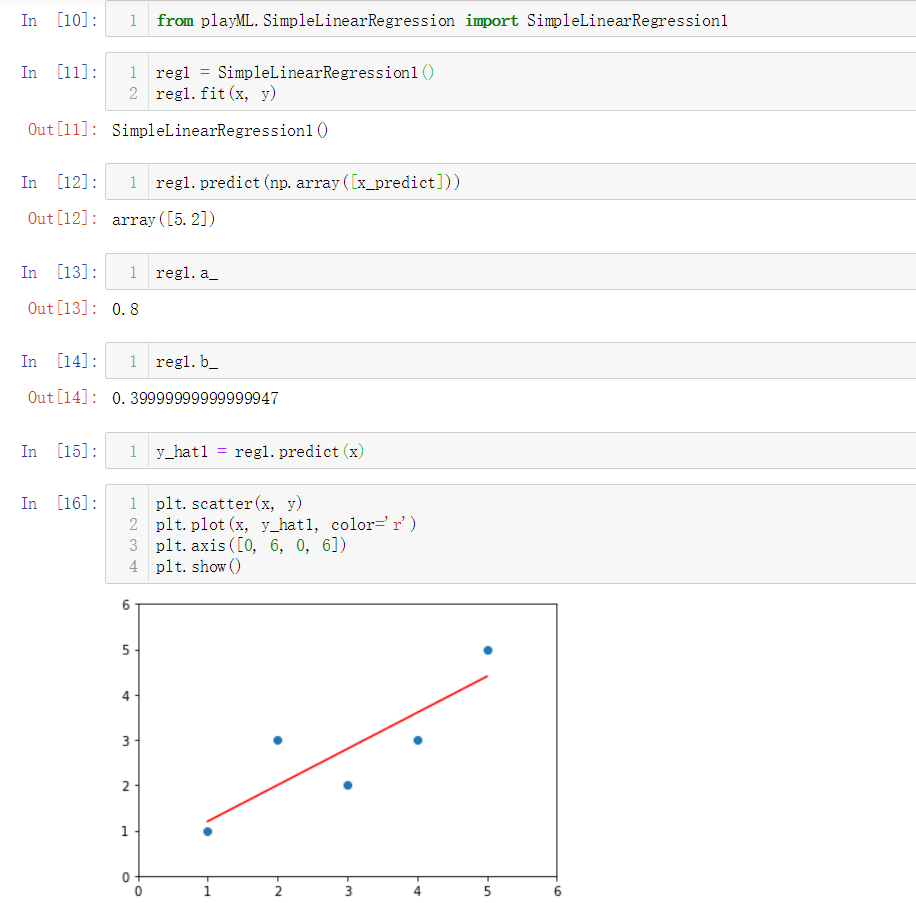
No.8. 将上述逻辑封装到一个SimpleLinearRegression1类中

No.9. 调用封装好的类
No.10. 向量化运算
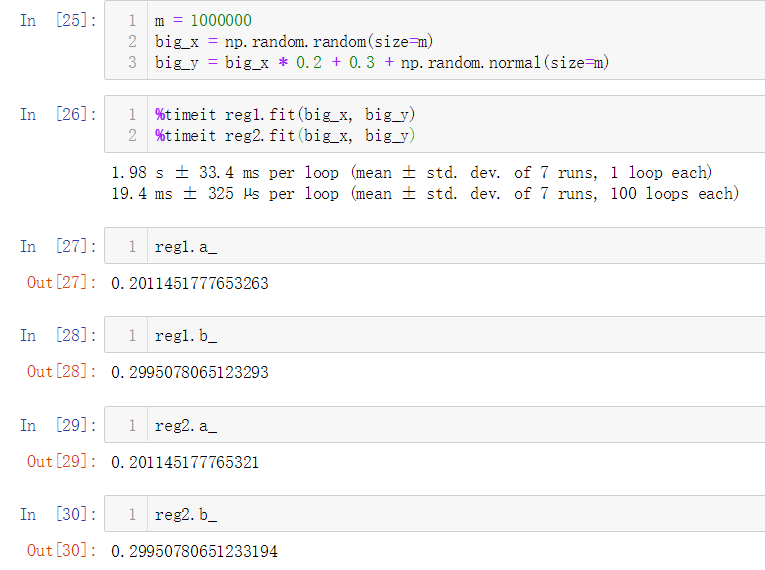
上面我们在计算参数 a 时使用了for循环,相较于for循环,向量之间相乘的效率要高很多,因此我们需要改进参数 a 的计算逻辑,采用向量化运算来提升性能。
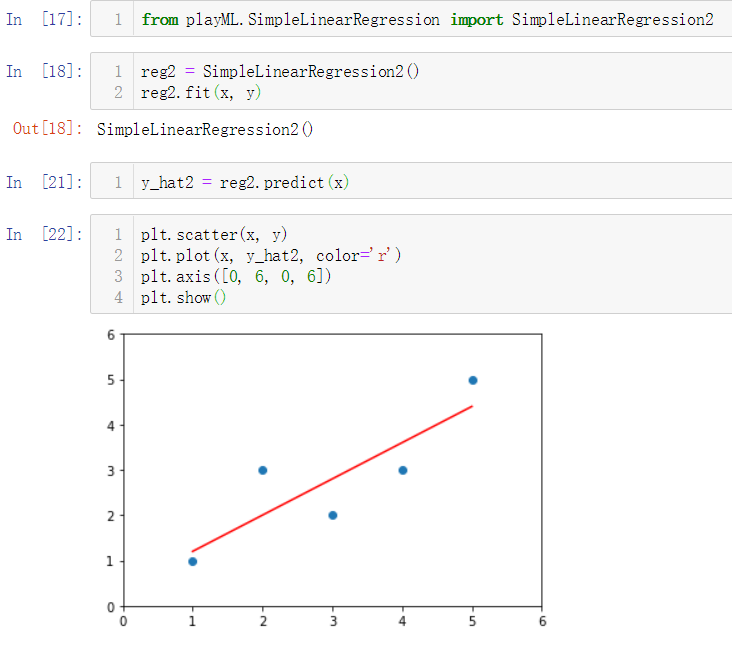
将类SimpleLinearRegression1中有关计算参数 a 的业务逻辑修改为如下,得到类SimpleLinearRegression2:

简单调用类SimpleLinearRegression2:
No.11. 简单测试for循环和向量化运算的性能差异
No.12. 衡量回归算法好坏的指标

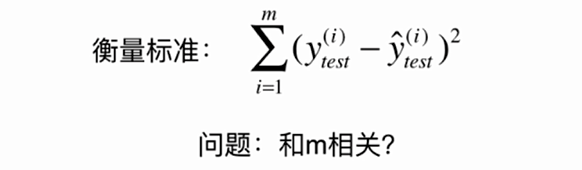



No.13. 用sklearn提供的波士顿房价数据集来实际衡量一下回归算法的好坏
准备工作
查看数据集的描述信息
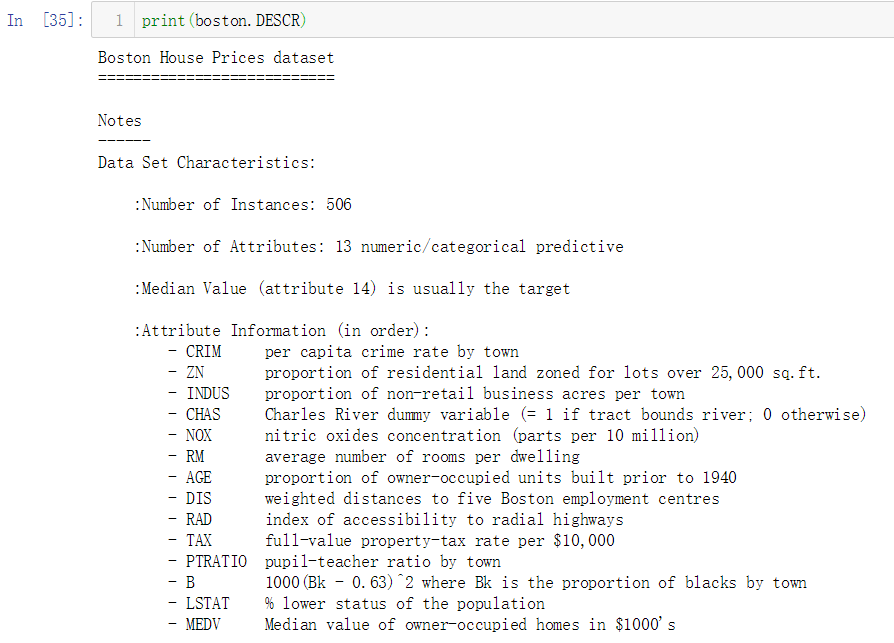
根据上面的信息,该数据集共有506个样本实例,每个样本共有13个特征
我们本次只测试简单线性回归,因此仅选取一个特征进行研究,选取'RM',即房间数量这一特征

'RM'这个特征的索引为5,我们所选取的数据如下:
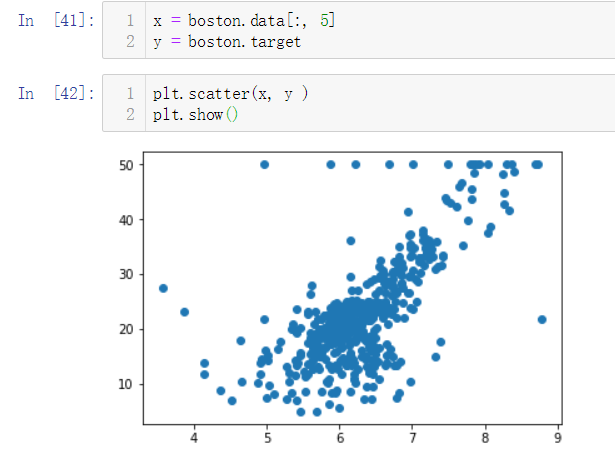
在上图中,纵坐标50的地方有很多点散列,这个很可能是数据上限造成的,我们需要剔除掉这些点。
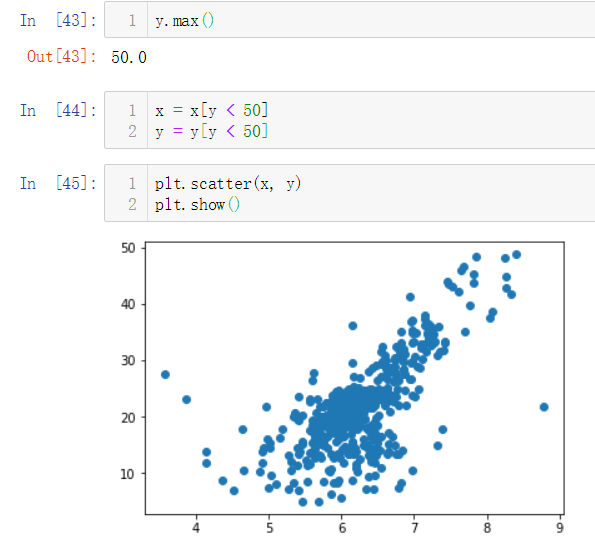
切分数据集、计算回归系数、计算误差的过程如下:
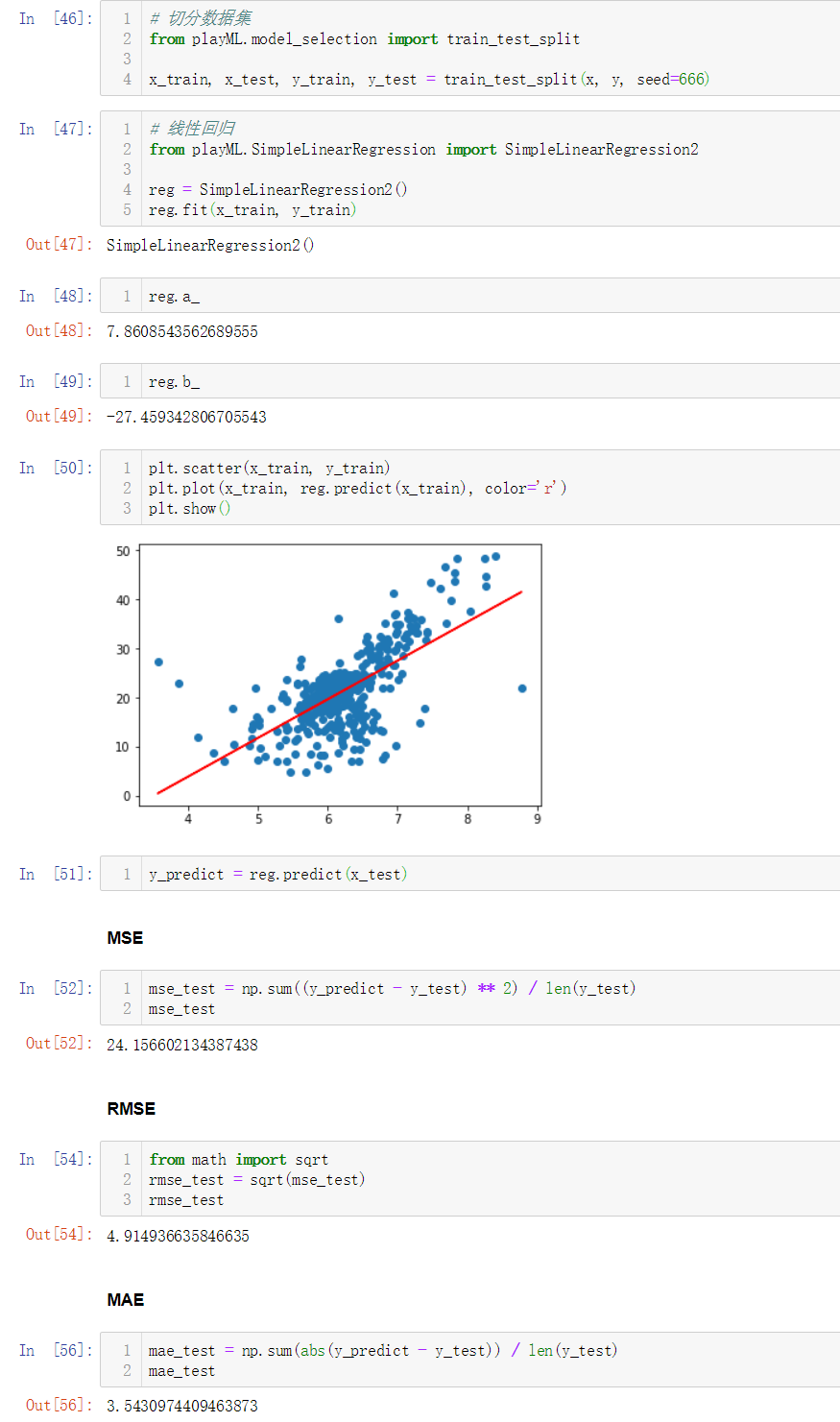
No.14. 封装三种误差计算方法的业务逻辑如下:

简单调用测试一下:
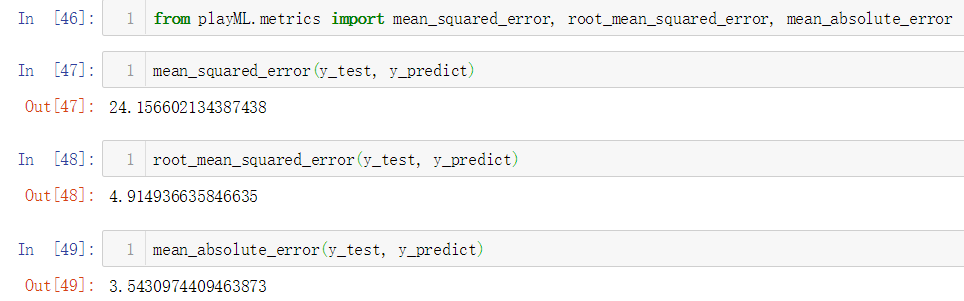
No.15. 调用sklearn中的MSE和MAE
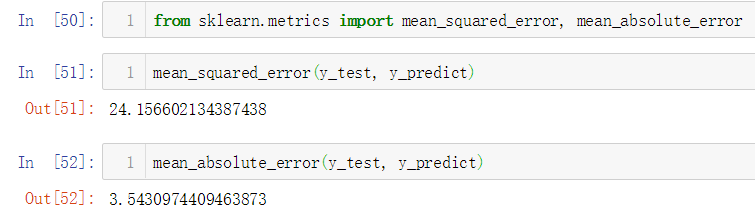
No.16. 最好的衡量线性回归的指标R Square

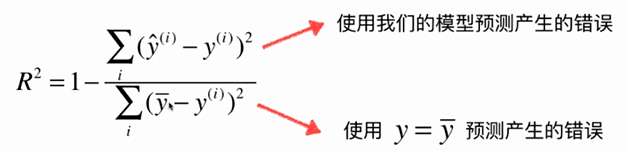

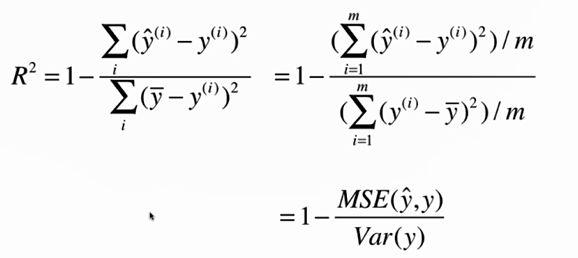
实际计算一下R Square

将其封装到一个函数中

调用一下:
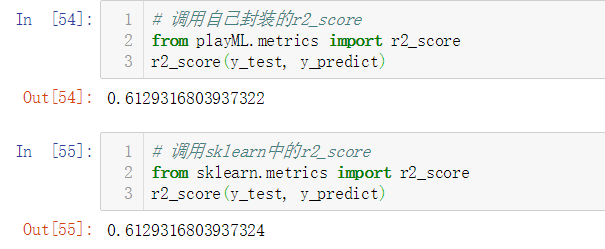
No.17. 最后,再往自定义的SimpleLinearRegression类中添加一个score方法,可以直接获取预测准确率,完整的业务逻辑如下:
