改进的迭代尺度法（Improved Iterative Scaling），在很多模型求解中用到，比如最大熵、CRFs等，对模型是对数线性模型的似然都适用。这个算法的思想也很简单，通俗的理解就是通过两个不等式变形优化下界，从而迭代到收敛的算法。
用到两个不等式，对 α>0 ：
(1)
对 p(x)是一个概率密度函数
(2)
这是文章中需要用到的两个不等式，先当做定理记下来吧。
CRF模型为：
其中Λ代表权值向量，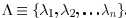
， ZΛ(x)是归一化因子。
似然函数可以写成：
其中
是样本（x,y）出现的频率。
接下来我们就是要找到合适的Λ向量。
我们假设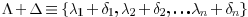
问题可以看做每次寻找一个Λ的移动向量，然后不断迭代，接下来就是确定每一步如何找到 ΔΛ .一种容易想到的做法就是通过最大化两次迭代的差值（因为这样可以保证不断接近似然函数的极大值），从而实现每一步得到最优的 ΔΛ。
对上面式子通过不等式 (1) 可以改写为：
定义：
于是我们得到：
（3）
对（3）应用不等式（2）可得：
（4）
综上，我们可以得到如下不等式：
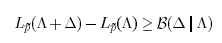
对（4）中不等号右边的式子求偏导（视δi是自变量）可得：
(5)
令(5)为0可以直接解出来δi , 从而不断迭代达到收敛。
参考：http://x-algo.cn/wp-content/uploads/2016/02/berger-iis.pdf