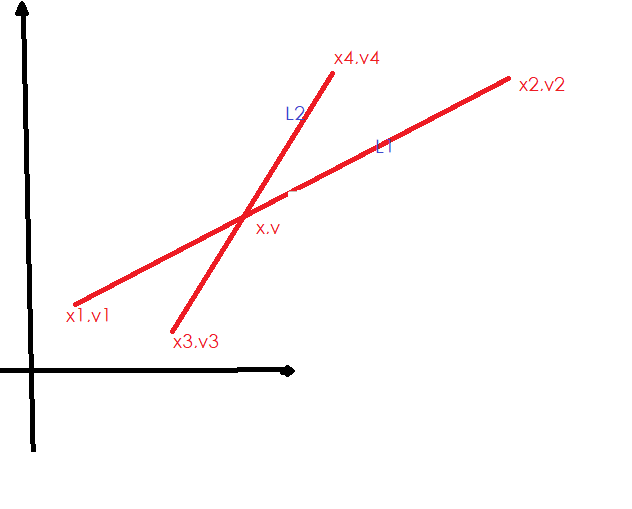
1.原理,直线上的一小段线段(起点到交叉点)的斜率=整个直线的斜率
x1,y1 x2,y2为一条直线起止点坐标
x3,y3 x4,y4为另一条直线起止坐标
设交点坐标为x,y 根据原理可得二元一次方程组

经过变化求得
x=(a*x1 - y1 + y3 - b*x3) / (a - b);
y= a * x - a * x1 + y1;
注意:

需考虑右侧等式分母为0的情况,即L1或L2垂直于x轴时,斜率不存在的情况
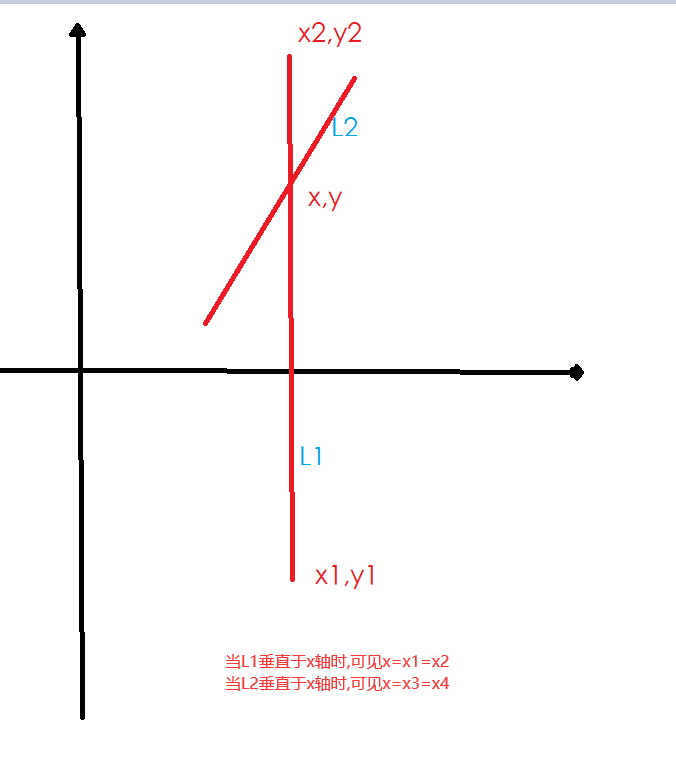
2.代码实现
double[] GetIntersectionPoint(double x1, double y1, double x2, double y2, double x3, double y3, double x4, double y4) { var a = (y2 - y1) / (x2 - x1); //需考虑分母不能为0 即x2=x1 l1垂直于x轴 var b = (y4 - y3) / (x4 - x3); //需考虑分母不能为0 即x4=x3 l2垂直于x轴 if (a == b) {//斜率相同,说明平行 无交点 throw new Exception("两直线平行,无交点"); } double x, y = 0; if (x2==x1) {//L1垂直于x轴 则x=x1=x2 a=infinity 想办法消除a x = x1; ////(y-y3)/(x-x3)=b 且x=x1 变换得y=bx1-bx3+y3 y = b*x1 - b*x3 + y3; return new double[] { x, y }; } if (x4==x3) {//L2垂直于x轴 则x=x3=x4 b=infinity x = x3; y = a * x - a * x1 + y1; return new double[] { x, y }; } x = (a*x1 - y1 + y3 - b*x3) / (a - b); y = a * x - a * x1 + y1; Log("[{lng:'"+x1+"',lat:'"+y1+"'},{lng:'"+x2+"',lat:'"+y2+"'},{lng:'"+x3+"',lat:'"+y3+"'},{lng:'"+x4+"',lat:'"+y4+"'},{lng:'"+x+"',lat:'"+y+"'}]"); return new double[] { x, y }; }