回归问题
常用均方误差
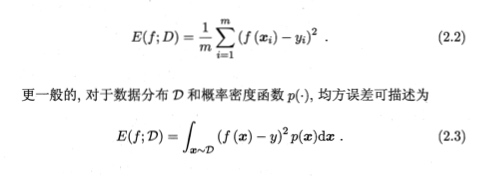 

分类问题
错误率与精度
 

其中 m 为样本的个数
查准率、查全率、F1
对于二分问题:
 

 

P-R曲线
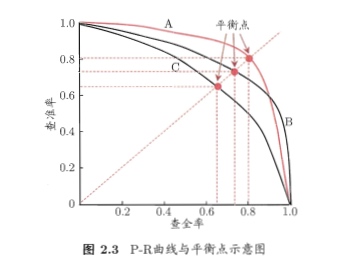 

- A优于C(A完全‘包住’C)
- A B 的比较可以比较图形下的面积
- 也可以基于平衡点(BEP)比较 A优于B
更好的比较实用下面的方式:
F1
 

加权形式:
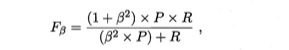 

 

 

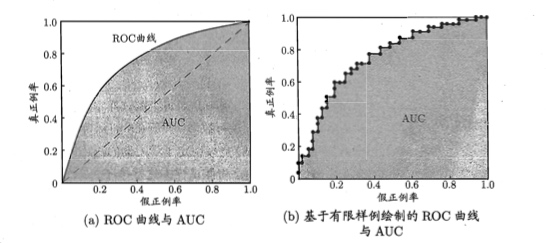
ROC AUC
ROC 受访者工作特征曲线
 

 

可以发现 TPR真正例率: 是真正例/正例的总和。
FPR假正例率:是假正例/反例的总数。

考虑ROC曲线图中的四个点和一条线。
- 第一个点,(0,1),即FPR=0, TPR=1,这意味着FN(false negative)=0,并且FP(false positive)=0。这是一个完美的分类器,它将所有的样本都正确分类。
- 第二个点,(1,0),即FPR=1,TPR=0,类似地分析可以发现这是一个最糟糕的分类器,因为它成功避开了所有的正确答案。
- 第三个点,(0,0),即FPR=TPR=0,即FP(false positive)=TP(true positive)=0,可以发现该分类器预测所有的样本都为负样本(negative)。
- 第四个点(1,1),分类器实际上预测所有的样本都为正样本。
我们可以断言,ROC曲线越接近左上角,该分类器的性能越好。
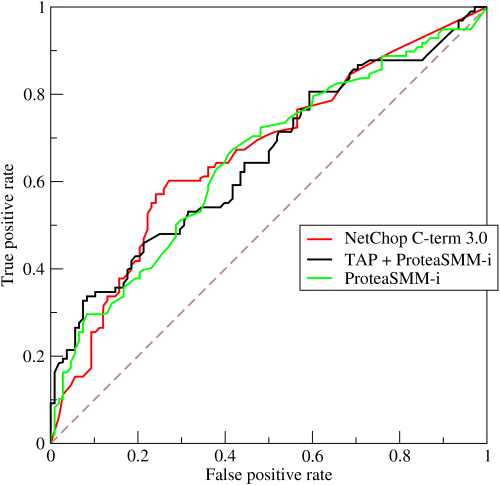 

考虑ROC曲线图中的虚线y=x上的点。这条对角线上的点其实表示的是一个采用随机猜测策略的分类器的结果,例如(0.5,0.5),表示该分类器随机对于一半的样本猜测其为正样本,另外一半的样本为负样本。
如何画ROC曲线、
分类器的一个重要功能“概率输出”,即表示分类器认为某个样本具有多大的概率属于正样本(或负样本)。通过更深入地了解各个分类器的内部机理,我们总能想办法得到一种概率输出。通常来说,是将一个实数范围通过某个变换映射到(0,1)区间
 

我们根据每个测试样本属于正样本的概率值从大到小排序。
图中共有20个测试样本,“Class”一栏表示每个测试样本真正的标签(p表示正样本,n表示负样本),“Score”表示每个测试样本属于正样本的概率4。
接下来,我们从高到低,依次将“Score”值作为阈值threshold
当测试样本属于正样本的概率大于或等于这个threshold时,我们认为它为正样本,否则为负样本。
举例来说,对于图中的第4个样本,其“Score”值为0.6,那么样本1,2,3,4都被认为是正样本,因为它们的“Score”值都大于等于0.6,而其他样本则都认为是负样本。
每次选取一个不同的threshold,我们就可以得到一组FPR和TPR,即ROC曲线上的一点。这样一来,我们一共得到了20组FPR和TPR的值,将它们画在ROC曲线的结果如下图:
 

当我们将threshold设置为1和0时,分别可以得到ROC曲线上的(0,0)和(1,1)两个点。将这些(FPR,TPR)对连接起来,就得到了ROC曲线。当threshold取值越多,ROC曲线越平滑。
AUC
AUC(Area Under Curve)被定义为ROC曲线下的面积,显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方,所以AUC的取值范围在0.5和1之间。使用AUC值作为评价标准是因为很多时候ROC曲线并不能清晰的说明哪个分类器的效果更好,而作为一个数值,对应AUC更大的分类器效果更好。
AUC值的含义是什么呢?
首先AUC值是一个概率值,当你随机挑选一个正样本以及一个负样本,当前的分类算法根据计算得到的Score值将这个正样本排在负样本前面的概率就是AUC值。当然,AUC值越大,当前的分类算法越有可能将正样本排在负样本前面,即能够更好的分类。
计算AUC
推荐使用sklearn中的包
 

 

为什么使用ROC和AUC呢?
既然已经这么多评价标准,为什么还要使用ROC和AUC呢?
因为ROC曲线有个很好的特性:当测试集中的正负样本的分布变化的时候,ROC曲线能够保持不变。
在实际的数据集中经常会出现类不平衡(class imbalance)现象,即负样本比正样本多很多(或者相反),而且测试数据中的正负样本的分布也可能随着时间变化。
下图是ROC曲线和Precision-Recall(P-R)曲线的对比:
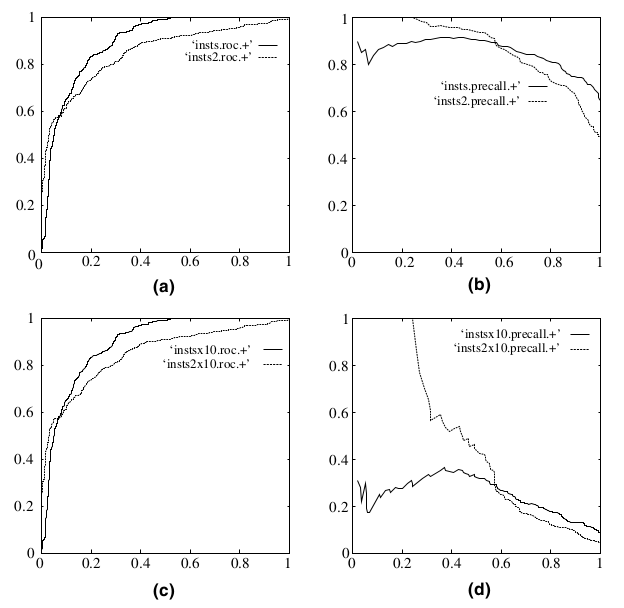 

在上图中,(a)和(c)为ROC曲线,(b)和(d)为Precision-Recall曲线。
(a)和(b)展示的是分类其在原始测试集(正负样本分布平衡)的结果,(c)和(d)是将测试集中负样本的数量增加到原来的10倍后,分类器的结果。可以明显的看出,ROC曲线基本保持原貌,而Precision-Recall曲线则变化较大。