算法
衡量算法的标准:
时间复杂度:程序执行的大概次数;O(1),O(n),O(logn),O(n^2)等
空间复杂度
排序算法:(外链)

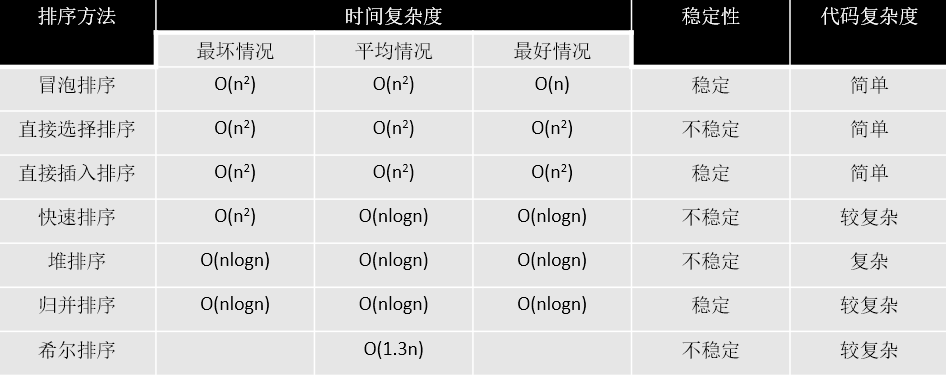
冒泡排序:
重复访问要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。访问数列的工作是重复地进行直到没有再需要交换的数据,也就是说该数列已经排序完成。

def BubbleSort(li): # 每一次生成一个最大值 for i in range(len(li)): #### i = 0 i = 1 --- 8 flag = False # 已生成最大值的便不用再遍历,且每次最后一个数不用 for j in range(len(li)-i-1): ### j = 0, 1, 2, 3, 7 if li[j] > li[j+1]: ### li[0] > li[1] | li[1] > li[2] | li[2] > li[3] li[j], li[j+1] = li[j+1], li[j] #### [5,4,6,7,3,8,2,1,9] flag = True if not flag: return
选择排序:
在未排序序列中找到最小(大)元素,存放到未排序序列的起始位置。在所有的完全依靠交换去移动元素的排序方法中,选择排序属于非常好的一种。

def selectSort(li): # 每次循环得到一个最小的数 for i in range(len(li)): # minLoc = i = 0 for j in range(i+1, len(li)): # j = 1, j = 2 if li[j] < li[i]: ### li[2] < li[minLoc] 4 < 5 li[j], li[i] = li[i], li[j] ## [5,7,4,6,3,8,2,9,1]
插入排序:
将数组中的所有元素依次跟前面已经排好的元素相比较,如果选择的元素比已排序的元素小,则交换,直到全部元素都比较过为止。

def insertSort(li): for i in range(1, len(li)): tmp = li[i] ## tmp = li[1] = 5 j = i - 1 ## j = 1 - 1 = 0 while j >= 0 and li[j] > tmp: ## li[0] = 7 > 5: li[j+1] = li[j] ## li[1] = li[0] = 7 ==> [7,7,4,6,3,8,2,9,1] j = j - 1 ## j = -1 li[j+1] = tmp ### li[0] = tmp = 5 ==> [5,7,4,6,3,8,2,9,1]
快速排序:
通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。

### 快排:O(n) def partition(li, left, right): tmp = li[left] while left < right: # 满足循环,左移;不满足条件时候,不进循环 while left < right and li[right] >= tmp: # 从右往左 right = right - 1 li[left] = li[right] # 满足循环,右移;不满足循环,不进循环 while left < right and li[left] <= tmp: left = left + 1 li[right] = li[left] # 指针重合,left,right均可以,为对称使用left li[left] = tmp return left ## 时间复杂度: O(nlogn) def quickSort(li, left, right): if left < right: mid = partition(li, left, right) ### O(n) quickSort(li, left, mid - 1) ### O(logn) quickSort(li, mid + 1, right)
归并排序:
分解:将列表越分越小,直至分成一个元素。
一个元素是有序的。
合并:将两个有序列表归并,列表越来越大

### 时间复杂度: O(nlogn) def merge(li, low, mid, right): i = low j = mid + 1 ltmp = [] while i <= mid and j <= right: if li[i] < li[j]: ltmp.append(li[i]) i = i + 1 else: ltmp.append(li[j]) j = j + 1 while i <= mid: ltmp.append(li[i]) i = i + 1 while j <= right: ltmp.append(li[j]) j = j + 1 li[low:right+1] = ltmp def mergeSort(li, low, high): if low < high: mid = (low + high) // 2 mergeSort(li, low, mid) mergeSort(li, mid + 1, high) print('归并之前:', li[low:high+1]) merge(li, low, mid, high) print('归并之后:', li[low:high + 1])
希尔排序:
希尔排序是一种分组插入排序算法。 首先取一个整数d1=n/2,将元素分为d1个组,每组相邻量元素之间距离为d1,在各组内进行直接插入排序; 取第二个整数d2=d1/2,重复上述分组排序过程,直到di=1,即所有元素在同一组内进行直接插入排序。 希尔排序每趟并不使某些元素有序,而是使整体数据越来越接近有序;最后一趟排序使得所有数据有序。
计数排序:

def countSort(li): count = [0 for i in range(11)] for index in li: count[index] += 1 li.clear() for index, val in enumerate(count): print(index, val) for i in range(val): li.append(index) li = [10,4,6,3,8,4,5,7] countSort(li) print(li)
堆排序:
大根堆:一棵完全二叉树,满足任一节点都比其孩子节点大
小根堆:一棵完全二叉树,满足任一节点都比其孩子节点小
1.建立堆 2.得到堆顶元素,为最大元素 3.去掉堆顶,将堆最后一个元素放到堆顶,此时可通过一次调整重新使堆有序。 4.堆顶元素为第二大元素。 5.重复步骤3,直到堆变空。
贪婪算法:

# 分糖果原则:贪婪算法 '''贪心规律 (1)某个糖果不能满足某个孩子,那么,该糖果一定不能满足更大需求因子的孩子。 (2)某个孩子可以用更小的糖果满足,则没必要用更大的糖果,留着更大的糖果去满足需求因子更大的孩子。(贪心!!) (3)孩子的需求因子更小则其更容易被满足,故优先从需求因子小的孩子开始,因为用一个糖果满足一个较大需求因子的孩子或满足较小需求因子的孩子效果一样。(最终总量不变)(贪心!!) 算法思路 (1)对需求因子数组g和糖果大小数组s进行从小到大排序; (2)按照从小到大的顺序使用各糖果,尝试是否可以满足某个孩子,每个糖果只尝试一次;若成功,则换下一个糖果尝试;直到发现没有孩子或者没有糖果,循环结束。 --------------------- ''' def candygivechildren(g, s): g = sorted(g) s = sorted(s) child = 0 cookie = 0 while child < len(g) and cookie < len(s): if g[child] < s[cookie]: child += 1 cookie += 1 return child g = [5,10,2,9,15,9] s = [1,3,6,8,20] res = candygivechildren(g,s) print(res)
查找算法:
顺序查找:

#### 时间复杂度:O(n) def linerSearch(li, val): for i in range(len(li)): if li[i] == val: return i
二分查找:

### 时间复杂度是: O(logn) def binarySearch(li, low, high, val): if low < high: mid = (low + high) // 2 if li[mid] == val: return mid elif li[mid] > val: binarySearch(li, low, mid, val) elif li[mid] < val: binarySearch(li, mid + 1, high, val) else: return -1
数据结构(外链)
研究数据存储和数据操作的一门学问!!!
线性结构:
数组:必须是连续的内存空间
优点:存取速度快
缺点:事先需要知道数组的长度
需要大块的连续内存
插入删除非常慢,效率极低
链表:离散存储
定义:
n个节点离散分配
彼此通过指针相连
每个节点只有一个前驱节点,每个节点只有一个后续节点
首节点没有前驱节点,尾节点没有后续节点
优点:空间没有限制,插入删除元素很快
缺点:查询比较慢

class Hero(object): def __init__(self, no=None, name=None, nickname=None, pNext=None): self.no = no self.name = name self.nickname = nickname self.pNext = pNext def add(head, hero): ### 后面添加 # head.pNext = hero # 将指针赋值给一个变量 cur = head # print(id(cur), id(head)) while cur.pNext != None: if cur.pNext.no > hero.no: break cur = cur.pNext hero.pNext = cur.pNext cur.pNext = hero # print(id(cur), id(head)) def showAll(head): cur = head while cur.pNext != None: cur = cur.pNext print(cur.no, cur.name) def delHero(head, no): cur = head while cur.pNext != None: if cur.pNext.no == no: break cur = cur.pNext ### cur += 1 cur.pNext = cur.pNext.pNext head = Hero() h1 = Hero(1, '宋江', '及时雨') add(head, h1) h2 = Hero(2, '卢俊义', '玉麒麟') add(head, h2) h4 = Hero(4, '鲁智深', '花和尚') add(head, h4) h3 = Hero(3, '林冲', '豹子头') add(head, h3) showAll(head)
data为自定义的数据,next为下一个节点的地址。

性能比较:
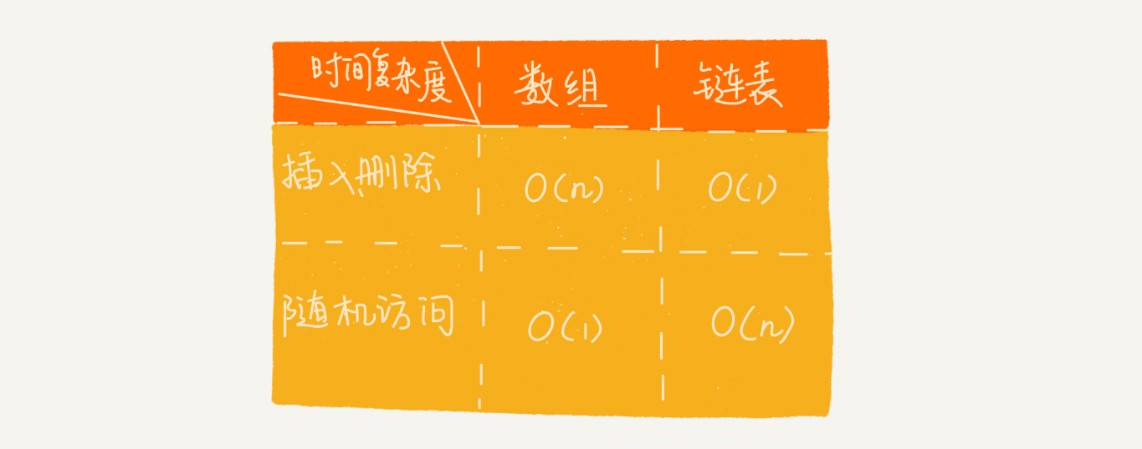
线性结构的两种应用方式:
栈:先进后出

函数调用
浏览器的前进或者后退
表达式求值
内存分配
队列:先进先出

你想看啥?
实际啥也没有
非线性结构:

树是数据库中数据组织的一种重要形式
操作系统子父进程的关系本身就是一颗树
面型对象语言中类的继承关系
树:
树有且仅有一个根节点
有若干个互不相交的子树,这些子树本身也是一颗树
度:子节点的个数
树的分类:
一般树
任意一个节点的子节点的个数不受限制
二叉树
定义:任意一个节点的子节点的个数最多是两个,且子节点的位置不可更改
满二叉树
定义:在不增加层数的前提下,无法再多添加一个节点的二叉树
完全二叉树
定义:只是删除了满二叉树最底层最右边连续的若干个节点
一般二叉树
森林
n个互不相交的树的集合
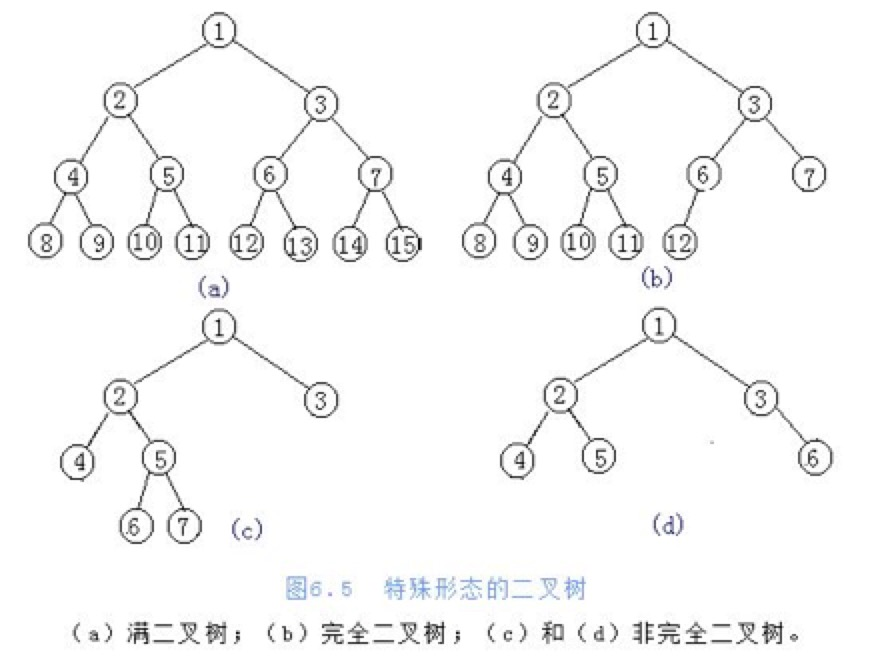
树的操作:
ps:不想写了,自己想象吧;
