1.简介
图(Graph)是由顶点的有穷非空集合和顶点之间的边的集合组成,通常表示为:G(V,E),G表示一个图,V是图G中顶点的集合,E是图G中边的集合。
图是一种复杂的非线性结构,在图结构中,每个元素都可以有零个多个前驱,也可以有零个或多个后继,元素之间的关系是任意的。
2.分类
图分无向图和有向图
无向图:由顶点和边构成;
有向图:由顶点和弧(有向边)构成,弧分弧头和弧尾
多重图:关联一对顶点的无向边(或有向边,边的方向一致)多于1条(称这些边为平行边)
简单图:既不含平行边也不含环的图成为简单图
(有向)完全图:如果任意两个顶点之间都存在边叫完全图,有向的边叫有向完全图
连通图:在无向图G中,任意两个顶点是相通的就是连通图
网:图中的边带权值的话,叫网
3.图的顶点和边
顶点的度:顶点关联边的数目
有向图中:入度,方向指向顶点的边;出度,方向背向顶点的边
路径长度:路径上边或弧的数目
4.存储结构
4.1.邻接矩阵
图的邻接矩阵存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息,一个二维数组(称为邻接矩阵)存储图中的边或弧的信息。
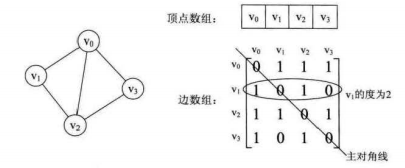
实际中,我们发现对于边数相对顶点较少的图,这种结构存在对存储空间的极大浪费。
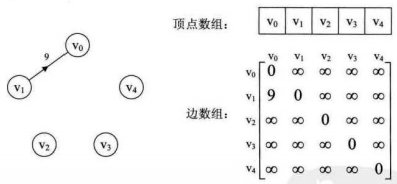
4.2.邻接表
图的邻接表存储方式是用一个一维数组存顶点,数组中每一项还需要存储指向下一个邻接点的指针,以便于查找该顶点的边信息。图中每个顶点的所有邻接点构成一个线性表,由于邻接点不定,故用单链表存储。
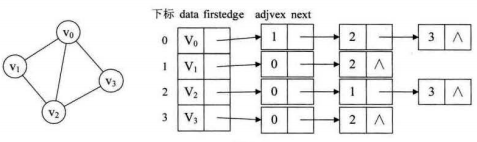
5.遍历
5.1.深度优先遍历
深度优先遍历(DFS,也称深度优先搜索):假设给定图G的初态是所有顶点均未曾访问过。在图G中任选一点Vi为初始出发点(源点),则深度优先遍历如下:首先访问出发点Vi,并将其标记为已访问过;然后依次从Vi出发探索Vi的每个邻接点Wj。若Wj未曾访问过,则以Wj为新的出发点继续进行深度优先遍历,直至图中所有与源点Vi有路径相通的顶点均已被访问为止。如此时图中任有未被访问的顶点,则另选一个尚未访问的顶点作为新的源点重复上述过程,直至图中所有顶点均已被访问为止。
5.2.广度优先遍历
广度优先遍历(BFS,也称广度优先搜索):这是一种盲目搜索法,它会系统的展开并检查图中的所有节点,不考虑搜索目标,一层一层逐层向下遍历,直至遍历完整张图。
参考资料:《大话数据结构》