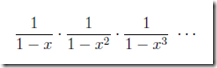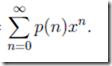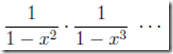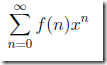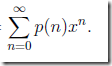整数划分 Integer Partition（二）

本文是整数划分的第二节，主要介绍整数划分的一些性质。

一

先来弥补一下上一篇文章的遗留问题：要求我们所取的 （n=m1+m2+...+mi ）中  m1 m2 ... mi连续，比如5=1+4就不符合要求了。这个时候的整数划分怎么操作呢？

这个问题的答案是这样的：

假设 n = r + (r + 1) + · · · + (r + k) ，我们需要找到所有的 r，这样我们就能获得划分数目了。

对上式进一步合并我们获得了 (2r + k)(k + 1) = 2n. 我们知道等式右面为一个偶数，而左边两个数的奇偶性是不一样的。所以问题就转化为找到一个奇数和一个偶数使其乘积为2n，这个奇数的种类数就是我们需要的，事实上这等于n的奇因数个数。

二

接着我们来看一下怎么用图形来表示整数划分：Ferrers Diagrams

比如10=5+3+1+1，那么我们就可以这样来表示：

从这样的表示中我们可以很显然获得一个结论：n的关于m的划分（n划分中的数不超过m）个数 等于 n的划分中元素个数为m个的划分数。

这个结论之所以很显然是因为我们只需要将上图旋转90度就可以获得 划分中元素个数为m的划分了；反之亦然。

三

求证：关于n的所有划分中不包含1的划分总个数 等于 n的划分总数减去n-1的划分总数，用式子我们可以这么来表示：

f(n) = p(n) − p(n − 1).

证明：

生成函数  =

               

               =

                 

                =

                  

当不允许使用1的时候，生成函数为 =

                                                    

                                                =

                                                   

                                                =

                                                  

故而有

                                                    =       (1-x) *    

所以，f(n) = p(n) − p(n − 1).

四 有多少种赋值方式（非负整数）使得 x1 + x2 + x3 + x4 + x5 + x6 = 32

解法一：

组合数学。32个球排成一行，插入五个隔板（可以理解为有标志的球）就可以获得我们需要的划分了，下图是一种划分，

•| • | • • • | • • • • • | • • • • • • • • • •| • • • • • • • • • • • •

答案是C₃₇⁵   ，注意一下底数是37而不是33。

解法二：