hdu4549 M斐波那契数列(矩阵快速幂+费马小定理)

M斐波那契数列

Problem Description

M斐波那契数列F[n]是一种整数数列，它的定义如下：
F[0] = a
F[1] = b
F[n] = F[n-1] * F[n-2] ( n > 1 )
现在给出a, b, n，你能求出F[n]的值吗？

 

Input

输入包含多组测试数据；
每组数据占一行，包含3个整数a, b, n（ 0 <= a, b, n <= 10^9 ）

 

Output

对每组测试数据请输出一个整数F[n]，由于F[n]可能很大，你只需输出F[n]对1000000007取模后的值即可，每组数据输出一行。

 

Sample Input

0 1 0

6 10 2

 

Sample Output

0

60

 

---

思路：

先将F[n]的前几项列出来，很容易发现规律: a¹  b¹  a¹b¹  a¹b²  a²b³ a³b⁵

 

a和b的指数是斐波那契数列，用矩阵快速幂可以求到F[n]里a和b的指数

 

然后再进行求模的处理

 

这是我第一次接触费马小定理，函数都是从博客上抄来的（QAQ）

 

费马小定理：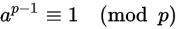 

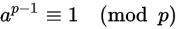
 即(a^p-1-1)%p=0

就可以得到aⁿ%p=(a^k*(p-1)*a^x)%p=(1^k*a^x)%p=a^x%p

即求a^x%p 先令x=x%(p-1)

再求a^x%p

 

---

AC代码：

#include<iostream>
#include<cstring>
using namespace std;
#define ll long long
const int maxn=2;
const int mod=1e9+7;
ll a,b,n;
ll Qpow(ll a,ll b){
    ll res=1;
    while(b){
        if(b&1)
        res=res*a%mod;
        a=a*a%mod;
        b>>=1;
    }
    return res;
}
struct matrix{
    ll a[maxn][maxn];
    matrix(){
        memset(a,0,sizeof(a));
    }
};

matrix mul(matrix a,matrix b){
    matrix res;
    for(int i=0;i<maxn;i++)
        for(int j=0;j<maxn;j++)
            for(int k=0;k<maxn;k++)
                res.a[i][j] = (res.a[i][j] + a.a[i][k] * b.a[k][j])%(mod-1);//费马小定理，这里是%(mod-1);
    return res;
}

matrix qpow(matrix A,ll m){//方阵A的m次幂
    matrix ans;
    for(int i=0;i<maxn;i++)
            ans.a[i][i]=1; //单位矩阵
    while(m){
        if(m&1)ans=mul(ans,A);
        A=mul(A,A);
        m>>=1;
    }
    return ans;
}
matrix x;
int main(){
    x.a[0][0]=1;x.a[0][1]=1;x.a[1][0]=1;x.a[1][1]=0;
    while(~scanf("%d %d %d",&a,&b,&n)){
        if(!a||!b){cout<<0<<endl;continue;}
        if(n==0){cout<<a<<endl;continue;}
        if(n==1){cout<<b<<endl;continue;}
        if(n==2){cout<<(a*b)%mod<<endl;continue;}
        matrix f=qpow(x,n-1);
        //cout<<f.a[0][0]<<' '<<f.a[0][1]<<endl;
        ll res=Qpow(a,f.a[0][1])*Qpow(b,f.a[0][0])%mod;
        cout<<res<<endl;
    }
}