6. Ensemble learning & AdaBoost

1. ensemble learning 集成学习

集成学习是通过构建并结合多个学习器来完成学习任务，如下图：

集成学习通过将多个学习学习器进行结合，常可以获得比单一学习器更优秀的泛化性能

从理论上来说，使用“弱学习器”集成足以获得好的性能，当实践中出于种种考虑，人们往往会使用比较强的学习器。

 

以下面为例，集成学习的结构通过投票法Voting（少数服从多数）产生：

由上面可以看出：个体学习器应该“好而不同”，即个体学习器要有一定的“准确性”，并且彼此间要有差异。

从理论上来说，假设个体学习器的误差 $epsilon$ 相互独立，那么随着集成中个体分类器数目 $T$ 的增加，集成的错误率将呈指数级下降。但现实任务中，个体学习器是为解决同一个问题而训练出来的，它们显然不可能相互独立。

根据个体学习器的生成方式，目前的集成学习方法大致分为两大类：
1. 个体学习器间存在强依赖关系，必须串行生成的序列化方法，如 Boosting
2. 个体学习器间不存在强依赖关系，可同时生成并行化方法，如Bagging 和 Random Forest

2. Boosting & AdaBoost

Boosting: 先从初始训练集训练一个基学习器，再根据学习器的表现对训练样本分布进行调整，使得先前基类学习器做错的训练样本在后续受到更多关注，然后基于调整后的样本分布来训练下一个基学习器；如此反复进行，直至基学习器达到事先指定值$T$，最终将这$T$个基学习器进行加权结合。

Boosting族算法中最著名的代表就是AdaBoost。

 

 

 

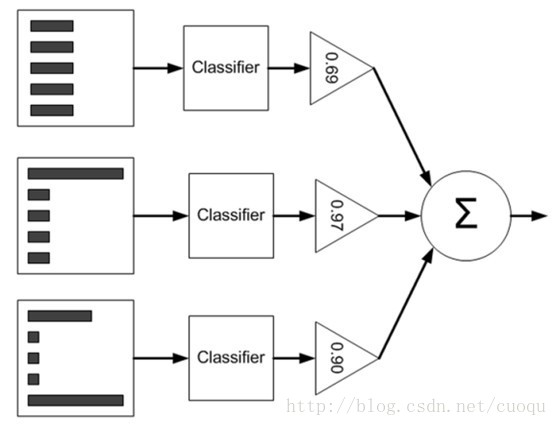
这是AdaBoost的原理示意图：左边矩形表示数据集$D$，中间是各个个体学习器，右边三角形是对每个弱学习器赋予的权重 $alpha$ ，最后根据每个弱学习器的加权组合来判断总体类别。要注意一下数据集从上到下三个矩形内直方图不一样，这表示每个样本的权重 $mathcal{D}$ 也发生了变化，样本的权重一开始初始化为相等的权重，然后根据弱学习器的错误率 $epsilon$ 来调整每个弱学习器的权重 $alpha$以及样本权重 $mathcal{D}$.

具体过程如下：

The error $epsilon$ is given by $epsilon = frac{number  of  incorrectly  classified  examples}{total  number  of  examples}$ and $alpha$ is given by $alpha = frac{1}{2}ln(frac{1-epsilon_t}{epsilon_t})$ $mathcal{D}_{t+1,i} = frac{mathcal{D}_{t,i}}{Z_t} { imes} e^{-alpha_t f(x_i) h_t(x_i)}$ $Z_t = sum_{i=1}^{m}mathcal{D}_{t,i} { imes} e^{-alpha_t f(x_i) h_t(x_i)}$ 1、弱分类器的选取 弱分类器的选取并没有一个特定的标准或选取准则，一般来说只要是能够实现基本的分类功能的分类器均可以作为adaboost中的弱分类器。 2、分类误差大于0.5，终止算法 分类误差大于0.5代表当前的分类器是否比随机预测要好，对于一个随机预测模型来说，其分类误差就是0.5，即一半预测对，一半预测错。若当前的弱分类器还没有随机预测的效果好，那便直接终止算法。但是当adaboost遇到这种情形时可能学习的迭代次数远远没有达到初始设置的迭代次数M，这可能会导致最终集成中只有很少的弱分类器，从而导致算法整体性能不佳。为了化解这种情况Kohavi在《Bias plus variance decomposition for zero-one loss functions》提出了用重采样法使得迭代过程重新启动。

3.多样性增强

　　在集成学习中需有效地生成多样性大的个体学习器。与简单地直接用初始数据训练出个体学习器相比，如何增强多样性呢？一般思路是在学习过程中引入随机性，常见做法主要是对数据样本、输入属性、输出表示、算法参数进行扰动。

数据样本扰动

给定初始数据集，可从中产生出不同的数据子集，再利用不同的数据子集训练出不同的个体学习器。数据样本扰动通常是基于采样法，例如在Bagging中使用自助采样，在Adaboost中使用序列采样。此类做法简单高效，使用最广。对很多常见的基学习器，例如决策树、神经网络等，训练样本稍加变化就会导致学习器有显著变动，数据样本扰动法对这样的“不稳定基学习器”很有效；然而，有一些基学习器对数据样本扰动不敏感，例如线性学习器、支持向量机、朴素贝叶斯、$k$近邻学习器等，这样的基学习器称为稳定基学习器，对此类基学习器进行集成往往需使用输入属性扰动等其他机制。

输入属性扰动

训练样本通常由一组属性描述，不同的“子空间”（subspace，即属性子集）提供了观察数据的不同视角。显然，从不同子空间训练出的个体学习器必然有所不同。著名的随机子空间（random subspace）算法就依赖于输入属性扰动，该算法从初始属性集中抽取出若干个属性子集，再基于每个属性子集训练一个基学习器。对于包含大量冗余属性的数据，在子空间中训练个体学习器不仅能产生多样性大的个体，还会因属性数的减少而大幅节省时间开销，同时，由于冗余属性多，减少一些属性后训练出的个体学习器也不至于太差。若数据只包含少量属性，或者冗余属性很少，则不宜使用输入属性扰动法。

输出表示扰动

此类做法的基本思路是对输出表示进行操纵以增强多样性，可对训练样本的类标记稍作变动，如“翻转法”随机改变一些训练样本的标记；也可对输出表示进行转化，如“输出调制法”将分类输出转化为回归输出后构建个体学习器；还可以将原任务拆解为多个可同时求解的子任务，如ECOC法利用纠错输出码将多分类任务拆解为一系列二分类任务来训练基学习器。

算法参数扰动

基学习算法一般都有参数需要进行设置，例如神经网络的隐含层神经元数、初始连接权值等，通过随机设置不同的参数，往往可产生差别较大的个体学习器。对参数较少的算法，可通过将其学习过程中某些环节用其他类似方式代替，从而达到扰动的目的，例如可以将决策树使用的属性选择机制替换成其他的属性选择机制。值得指出的是，使用单一学习器时通常需要使用交叉验证等方法来确定参数值，这事实上已使用了不同参数训练出多个学习器，只不过最终仅选择其中一个学习器进行使用，而集成学习则相当于把这些学习器都利用起来；由此可以看出，集成学习技术的实际计算开销并不比使用单一学习器大很多。

参考：

周志华 机器学习

Zhou, Ensemble Method: Foundations and Algorithms.

http://blog.csdn.net/sinat_17451213/article/details/51055718

http://blog.csdn.net/marvin521/article/details/9319459

http://blog.csdn.net/autocyz/article/details/51305999