信息传递

这里给大家介绍一种奇怪的做法，为什么奇怪呢，因为这玩意儿又不像并查集，又不像拓扑序

（其实是我模拟赛的时候先想的拓扑序，又想的并查集，然后一步步改成了现在这个样子）

思路

1. 首先，我们通过题目，发现这是一个有向非联通图，且每个点有且仅有一条出边。

2. 其次，答案只会存在于以下两种情况中

   

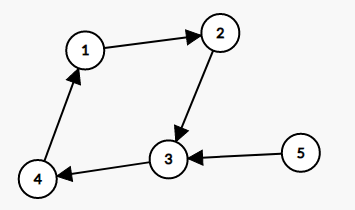
   图一

   

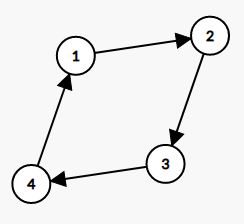
   图二

(3.;)一般我们使用拓扑序时，是要从入度为 (0) 的点开始遍历，但是显然下面这张图不会被遍历到，那如果从入度为 (1) 的点开始呢？

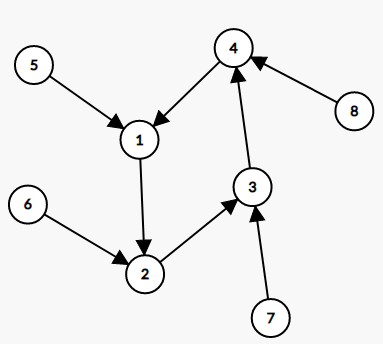
(4.;)那么这张图也显然，只有入度为 (0) 和 (2) 的点，以此类推，单纯从任何一种入度为某个值的点开始遍历是不合适的。

(5.;)所以我们还是考虑最上面两张基本的图，图一带着个“小尾巴”，一定有入度为 (0) 的点；图二本身是一个大环，只有入度为 (1) 的点
(6.;)如果一遍不行，为什么不遍历两遍呢？思路也就出来了。

实现

关于实现，我在模拟赛时还发现了两个小问题

1. 如果对每一个点判断，然后遍历，时间复杂度比较高，可能会 (TLE)，我在模拟的时候先打了这个复杂度较高的算法，时间复杂度大概是 (O(n^2))，这样交上去是有风险的，宁愿要一个常数大一点的 (O(n)) 算法，咱也不能 (T) 是不是？

$Sol: $ 所以我们在两次遍历前，各预处理一下，处理掉没用的点，之后在剩下的点里面选起点遍历就好了。

2. 多次访问到同一个点导致答案被不正确地更新如何处理

(Sol:) 我用一个数组，记录一个点是被哪次的 (DFS) 遍历的，另外，由于我懒，我没有新开数组，而是用的入度 (in) 数组，又防止混淆，我用的负数，下面举个栗子

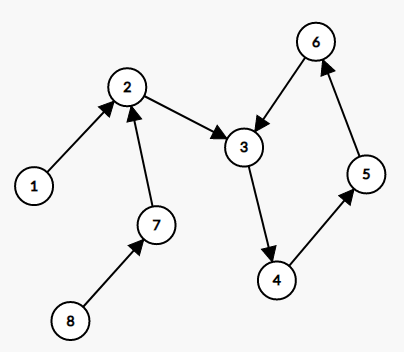
第一步，从 (1) 开始遍历， (1,2,3,4,5,6) 的 (in) 数组均被更新成 (-1)，第二次从 (8) 开始，(8,7) 被更新为 (-2)，这时遍历到 (2)，经过判断，(in[7] ot=in[2])，不更新答案

Code

各变量表示：

(cnt, tot) 计数用

(to) 每个点指向的节点

(vis) 判断是否被遍历过，顺便记录深度

(in) 初期是每个点的入度，后期也变成了一个判断数组

(zero) 记录入度为 (0) 的点

(one) 记录入度为 (1) 的点

代码自认为可读性较高

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <algorithm>
using namespace std;
const int N = 200005;
int cnt, to[N], n, vis[N], ans = 1000000007, in[N], zero[N], one[N];

void dfs(int k, int tot)
{
	if(vis[to[k]] && in[to[k]] == tot)
		ans = min(ans, vis[k] + 1 - vis[to[k]]);
	else if(vis[to[k]] && in[to[k]] != tot)
		return;
	else {
		vis[to[k]] = vis[k] + 1;
		in[to[k]] = tot;
		dfs(to[k], tot);
	}
}

int main()
{
//	freopen("message.in", "r", stdin);
//	freopen("message.out", "w", stdout);
	cin >> n;
	for(int i = 1; i <= n; i++) {
		cin >> to[i];
		in[to[i]]++;
	}
	cnt = 0;
	for(int i = 1; i <= n; i++) {
		if(in[i] == 0 && vis[i] == 0) {
			zero[++cnt] = i;
		}
	}
	int tot = 0;
	for(int i = 1; i <= cnt; i++) {
		if(vis[zero[i]] == 0) {
			vis[zero[i]] = 1;
			dfs(zero[i], --tot);
		}
	}
	cnt = 0;
	for(int i = 1; i <= n; i++) {
		if(in[i] == 1 && vis[i] == 0) {
			one[++cnt] = i;
		}
	}
	for(int i = 1; i <= cnt; i++) {
		if(vis[one[i]] == 0) {
			vis[one[i]] = 1;
			in[one[i]] = 1;
			dfs(one[i], 1);
		}
	}
	cout << ans << "
";
//	fclose(stdin);
//	fclose(stdout);
	return 0;
}