

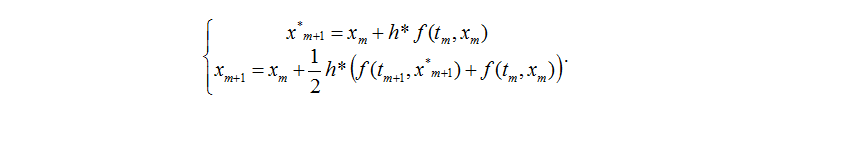


一、显示Euler
函数文件:Euler.m
1 function f=Euler(h,Y) 2 f(1,1)=Y(1)+h*(0.01-(1+(Y(1)+1000)*(Y(1)+1))*(0.01+Y(1)+Y(2))); 3 f(2,1)=Y(2)+h*(0.01-(1+Y(2)^2)*(0.01+Y(1)+Y(2)));
脚本文件:
1 tic; 2 clear 3 clc 4 %% 5 %显示Euler方法求刚性微分方程,要求用Richardson外推法估计近似误差从而控制步长 6 y(1:2,1)=[0;0];%初值 7 e=1e-5;%误差过小 8 tol=1e-3;%指定的误差 9 N=10;%节点的步数 10 h=1/N;%初始步长 11 t(1)=0; 12 i=1; 13 while t(i)+h<=1 14 k=1; 15 %%自动变步长 16 while k==1 17 y(1:2,i+1)=Euler(h,y(1:2,i));%符合误差的数值解 18 y1_half=Euler(h/2,y(1:2,i));%半步长的中点数值解 19 y1_one=Euler(h/2,y1_half);%半步长的右端点的数值解 20 Estimate_error=2*norm(y(1:2,i+1)-y1_one);%中间估计误差 21 if Estimate_error<tol%指定误差 22 k=0;%步长相差不大,或者说正好在指定的误差范围内,则确定选择h作为步长。 23 elseif Estimate_error<e%误差过小 24 h=2*h; 25 else 26 h=h/2; 27 end 28 end 29 t(i+1)=t(i)+h; 30 i=i+1; 31 end 32 %% 33 %绘图 34 plot(t,y,''); 35 xlabel('t'),ylabel('y(t) and z(t)'); 36 legend('y(t)','z(t)'); 37 title('Implicit Euler method for numerical solution of image'); 38 grid on; 39 toc;
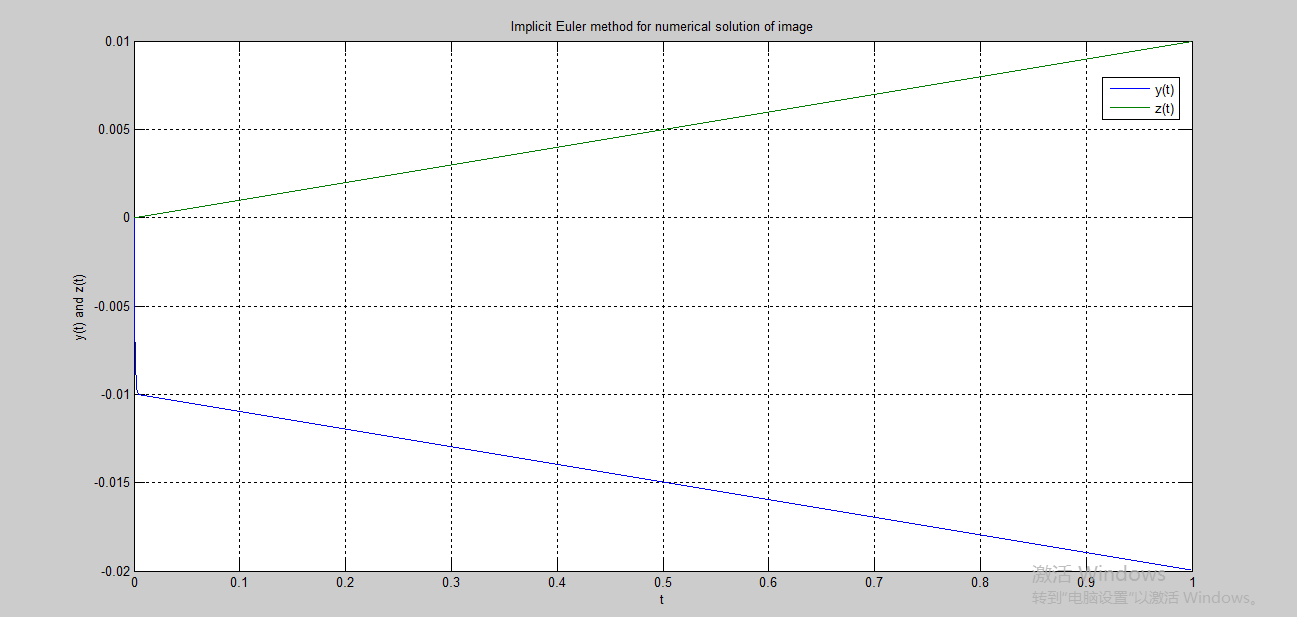
效果图:
二、隐式Euler:Euler.m
1 function X=Euler(t_h,u) 2 %隐式Euler(Newton迭代法) 3 %% 4 Tol=1e-5; 5 U=u; 6 x1=U-Jacobian(U,t_h)F(U,u,t_h); 7 while (norm(x1-U,2)>=Tol) 8 %数值解的2范数是否在误差范围内 9 U=x1; 10 x1=U-Jacobian(U,t_h)F(U,u,t_h); 11 end 12 X=x1;%不动点 13 %雅可比矩阵 14 function f=Jacobian(U,t_h) 15 f(1,1)=-t_h*((2*U(1)+1001)*(0.01+U(1)+U(2))+1+(U(1)+1000)*(U(1)+1))-1; 16 f(1,2)=-t_h*(1+(U(1)+1000)*(U(1)+1)); 17 f(2,1)=-t_h*(1+U(2)^2); 18 f(2,2)=-t_h*(2*U(2)*(0.01+U(1)+U(2))+(1+U(2)^2))-1; 19 20 %方程组 21 %% 22 function fun=F(U,u,t_h) 23 fun(1,1)=u(1)+t_h*(0.01-(1+(U(1)+1000)*(U(1)+1))*(0.01+U(1)+U(2)))-U(1); 24 fun(2,1)=u(2)+t_h*(0.01-(1+U(2)^2)*(0.01+U(1)+U(2)))-U(2);
脚本文件:
1 tic; 2 clear 3 clc 4 %隐式Euler方法求刚性微分方程,要求用Richardson外推法估计近似误差从而控制步长 5 %% 6 y(1:2,1)=[0;0];%初值 7 e=1e-5;%误差过小 8 tol=1e-3;%指定的误差 9 N=100;%节点的步数 10 h=1/N;%初始步长 11 t(1)=0;%初始节点 12 i=1; 13 while t(i)+h<=1 14 k=1; 15 %自动变步长 16 while k==1 17 y(1:2,i+1)=Euler(h,y(1:2,i));%符合误差的数值解 18 % y1_half=Euler(h/2,y(1:2,i));%半步长的中点数值解 19 y1_half=Euler(h/2,y(1:2,i));%半步长的右端点的数值解 20 Estimate_error=2*norm(y(1:2,i+1)-y1_half);%中间估计误差 21 if Estimate_error<tol%指定误差 22 k=0;%步长相差不大,或者说正好在指定的误差范围内,则确定选择h作为步长。 23 elseif Estimate_error<e%误差过小 24 h=2*h; 25 else%近似估计误差大于指定误差 26 h=h/2; 27 end 28 end 29 t(i+1)=t(i)+h; 30 i=i+1; 31 end 32 %绘图 33 %% 34 plot(t,y); 35 xlabel('t'),ylabel('y(t) and z(t)'); 36 legend('y(t)','z(t)'); 37 title('Explicit Euler method for numerical solution of image'); 38 grid on ; 39 toc;
效果图:
