C#数据结构-线索化二叉树

为什么线索化二叉树？

对于二叉树的遍历，我们知道每个节点的前驱与后继，但是这是建立在遍历的基础上,否则我们只知道后续的左右子树。现在我们充分利用二叉树左右子树的空节点，分别指向当前节点的前驱、后继，便于快速查找树的前驱后继。

不多说，直接上代码：

/// <summary>
/// 线索二叉树 节点
/// </summary>
/// <typeparam name="T"></typeparam>
public class ClueTreeNode<T>
{
    /// <summary>
    /// 内容
    /// </summary>
    public T data { get; set; }
    /// <summary>
    /// 左树
    /// </summary>
    public ClueTreeNode<T> leftNode { get; set; }
    /// <summary>
    /// 右树
    /// </summary>
    public ClueTreeNode<T> rightNode { get; set; }
    /// <summary>
    /// 0 标识左树 1 标识 当前节点的前驱
    /// </summary>
    public int leftTag { get; set; }
    /// <summary>
    /// 0标识右树 1 标识 当前节点的后继
    /// </summary>
    public int rightTag { get; set; }

    public ClueTreeNode()
    {
        data = default(T);
        leftNode = null;
        rightNode = null;
    }

    public ClueTreeNode(T item)
    {
        data = item;
        leftNode = null;
        rightNode = null;
    }
}

/// <summary>
/// 线索化 二叉树 
/// 
/// 为什么线索化二叉树？
/// 第一：对于二叉树，如果有n个节点，每个节点有指向左右孩子的两个指针域，所以一共有2n个指针域。
/// 而n个节点的二叉树一共有n-1条分支线数，也就是说，其实是有 2n-(n-1) = n+1个空指针。
/// 这些空间不存储任何事物，白白浪费内存的资源。
/// 第二：对于二叉树的遍历，我们知道每个节点的前驱与后继，但是这是建立在遍历的基础上。
/// 否则我们只知道后续的左右子树。
/// 第三：对于二叉树来说，从结构上来说是单向链表，引入前驱后继后，线索化二叉树可以认为是双向链表。
/// </summary>
/// <typeparam name="T"></typeparam>
public class ClueBinaryTree<T>
{
    /// <summary>
    /// 树根节
    /// </summary>
    private ClueTreeNode<T> head { get; set; }
    /// <summary>
    /// 线索化时作为前驱转存
    /// </summary>
    private ClueTreeNode<T> preNode { get; set; }

    public ClueBinaryTree(){
        head = new ClueTreeNode<T>();
    }
    public ClueBinaryTree(T val){
        head = new ClueTreeNode<T>(val);
    }


    public ClueTreeNode<T> GetRoot(){
        return head;
    }

    /// <summary>
    /// 插入左节点
    /// </summary>
    /// <param name="val"></param>
    /// <param name="node"></param>
    /// <returns></returns>
    public ClueTreeNode<T> AddLeftNode(T val, ClueTreeNode<T> node){
        if (node == null)
            throw new ArgumentNullException("参数错误");
        ClueTreeNode<T> treeNode = new ClueTreeNode<T>(val);
        ClueTreeNode<T> childNode = node.leftNode;
        treeNode.leftNode = childNode;
        node.leftNode = treeNode;
        return treeNode;
    }

    /// <summary>
    /// 插入右节点
    /// </summary>
    /// <param name="val"></param>
    /// <param name="node"></param>
    /// <returns></returns>
    public ClueTreeNode<T> AddRightNode(T val, ClueTreeNode<T> node){
        if (node == null)
            throw new ArgumentNullException("参数错误");
        ClueTreeNode<T> treeNode = new ClueTreeNode<T>(val);
        ClueTreeNode<T> childNode = node.rightNode;
        treeNode.rightNode = childNode;
        node.rightNode = treeNode;
        return treeNode;
    }
    /// <summary>
    /// 删除当前节点的 左节点
    /// </summary>
    /// <param name="node"></param>
    /// <returns></returns>
    public ClueTreeNode<T> DeleteLeftNode(ClueTreeNode<T> node){
        if (node == null || node.leftNode == null)
            throw new ArgumentNullException("参数错误");
        ClueTreeNode<T> leftChild = node.leftNode;
        node.leftNode = null;
        return leftChild;
    }

    /// <summary>
    /// 删除当前节点的 右节点
    /// </summary>
    /// <param name="node"></param>
    /// <returns></returns>
    public ClueTreeNode<T> DeleteRightNode(ClueTreeNode<T> node){
        if (node == null || node.rightNode == null)
            throw new ArgumentNullException("参数错误");
        ClueTreeNode<T> rightChild = node.rightNode;
        node.rightNode = null;
        return rightChild;
    }



    /// <summary>
    /// 中序遍历线索化二叉树
    /// </summary>
    public void MiddlePrefaceTraversal(){
        ClueTreeNode<T> node = head;
        while (node != null)
        {
            //判断是否是
            while (node.leftTag == 0)
            {
                node = node.leftNode;
            }
            Console.Write($" {node.data}");
            while (node.rightTag == 1)
            {
                node = node.rightNode;
                Console.Write($" {node.data}");
            }
            node = node.rightNode;
        }
    }
    /// <summary>
    /// 线索化二叉树
    /// </summary>
    /// <param name="node"></param>
    public void MiddleClueNodes(ClueTreeNode<T> node){
        if (node == null)
        {
            return;
        }
        //线索化左子树
        MiddleClueNodes(node.leftNode);
        //当左树为空时，指向前驱，标识为 1
        if (node.leftNode == null)
        {
            node.leftNode = preNode;
            node.leftTag = 1;
        }
        //如果 前驱的右树不为空
        if (preNode != null && preNode.rightNode == null)
        {
            preNode.rightNode = node;
            preNode.rightTag = 1;
        }
        preNode = node;
        //线索化右子树
        MiddleClueNodes(node.rightNode);
    }
}

 

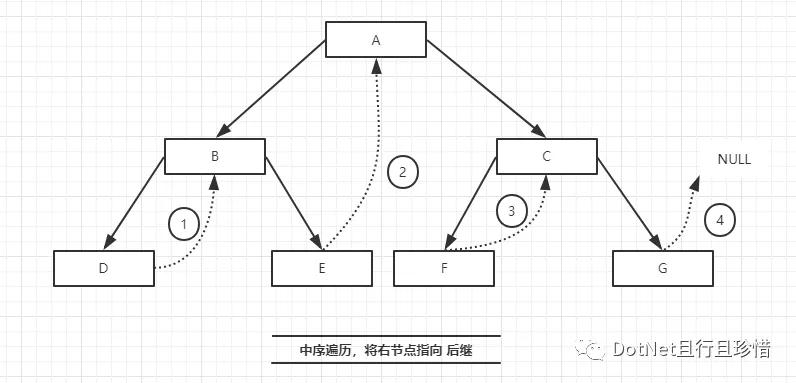
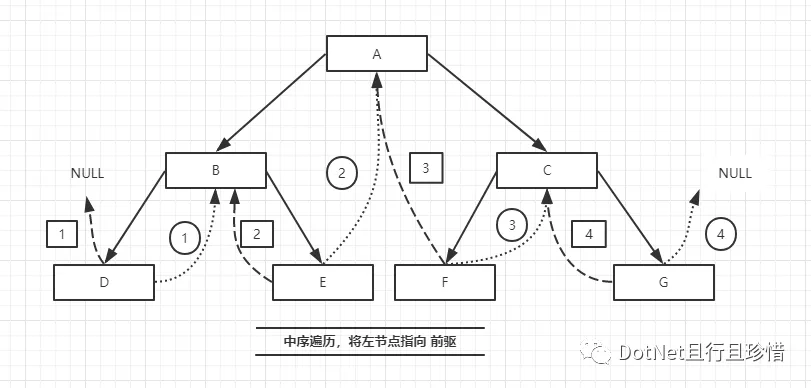
 现在我们测试：

//创建树
ClueBinaryTree<string> clueBinaryTree = new ClueBinaryTree<string>("A");
ClueTreeNode<string> tree1 = clueBinaryTree.AddLeftNode("B", clueBinaryTree.GetRoot());
ClueTreeNode<string> tree2 = clueBinaryTree.AddRightNode("C", clueBinaryTree.GetRoot());
ClueTreeNode<string> tree3 = clueBinaryTree.AddLeftNode("D", tree1);
clueBinaryTree.AddRightNode("E", tree1);
clueBinaryTree.AddLeftNode("F", tree2);
clueBinaryTree.AddRightNode("G", tree2);

clueBinaryTree.MiddleClueNodes(clueBinaryTree.GetRoot());

Console.Write("中序遍历");
clueBinaryTree.MiddlePrefaceTraversal();

打印结果：

中序遍历 D B E A F C G