LSSS 方案采用 Zhen Liu, Zhenfu Cao在2010年提出的方法。
论文:Liu, Z., Cao, Z., Duncan S.W.: Efficient generation of linear secret sharing scheme matrices from threshold access trees. IACR ePrint Achieve, (2010) 374.
关于里面提到的访问控制的几种形式,就不一一说明了,论文里面讲解的很清楚,阅读起来也相对简单。这里仅对文中提出的 LSSS 方案构造举例进行进一步说明。
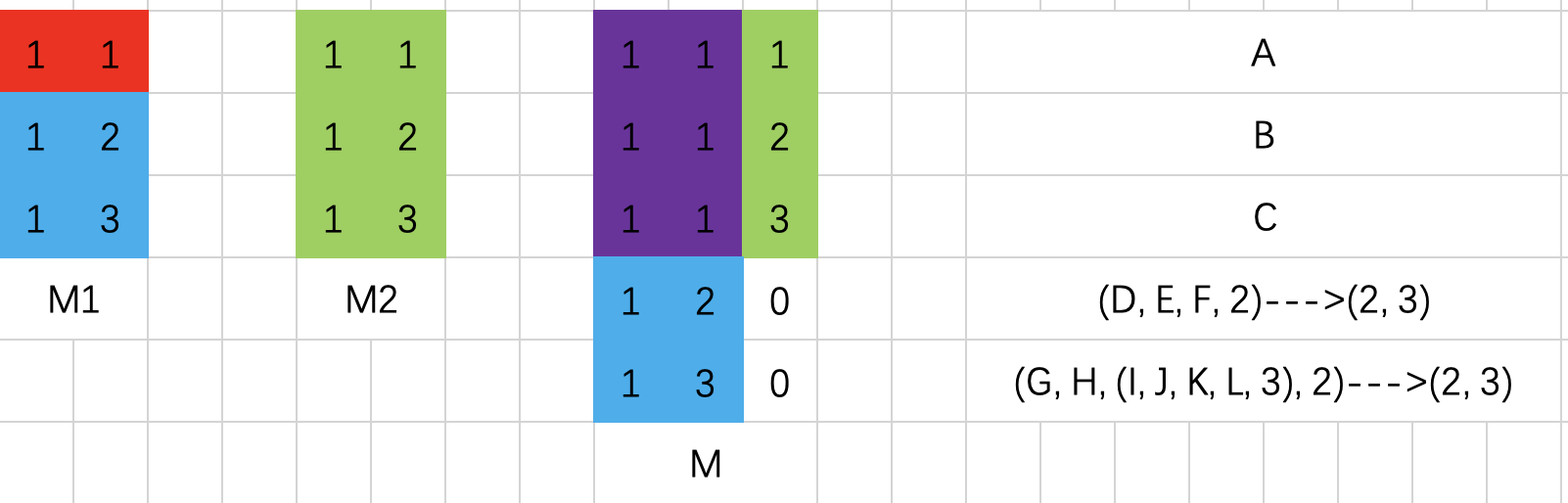
《前提说明:图中 红色为被替换、蓝色为保留、紫色为计算得到、绿色为替换部分》
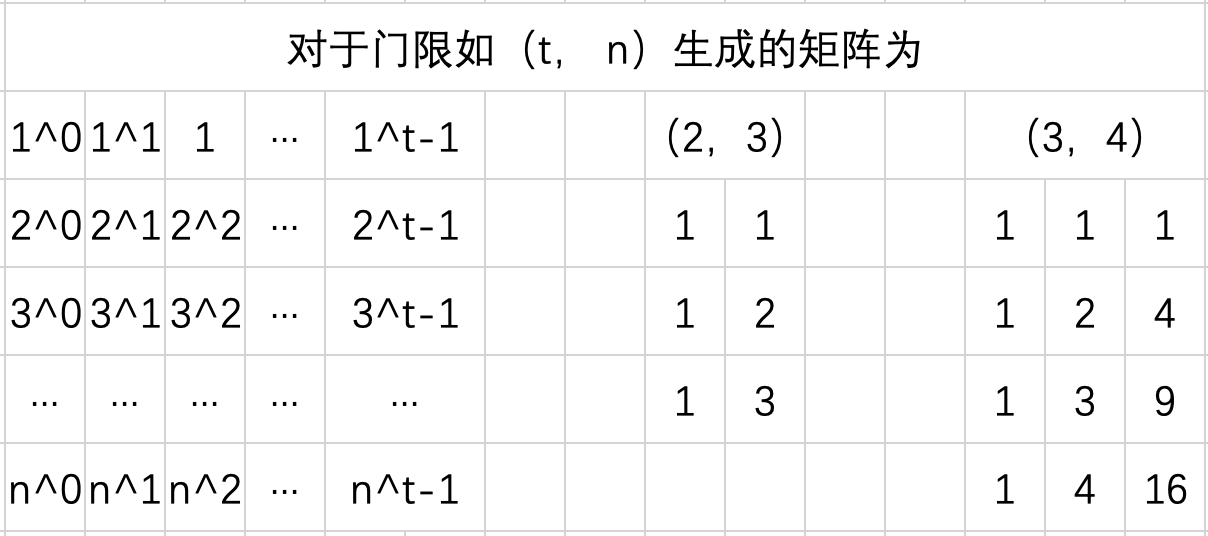
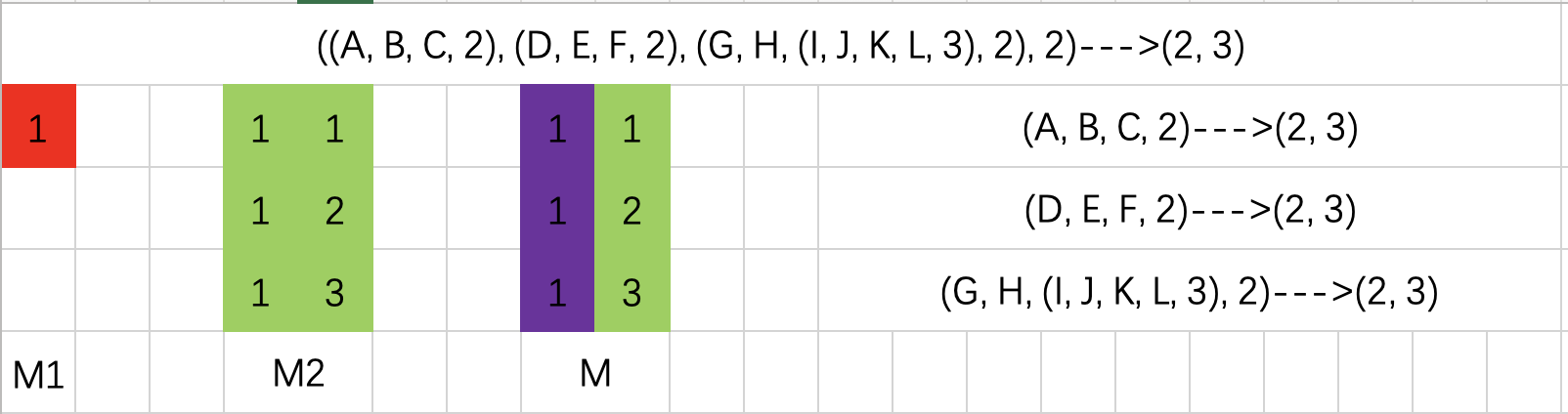
文中 访问策略描述为 ((A, B, C, 2), (D, E, F, 2), (G, H, (I, J, K, L, 3), 2), 2),对相对应行进行插入操作。插入的矩阵生成的方法为:
接下来为文中生成 LSSS 矩阵的过程 ,
M1 为原矩阵,M2 为生成的替换矩阵。
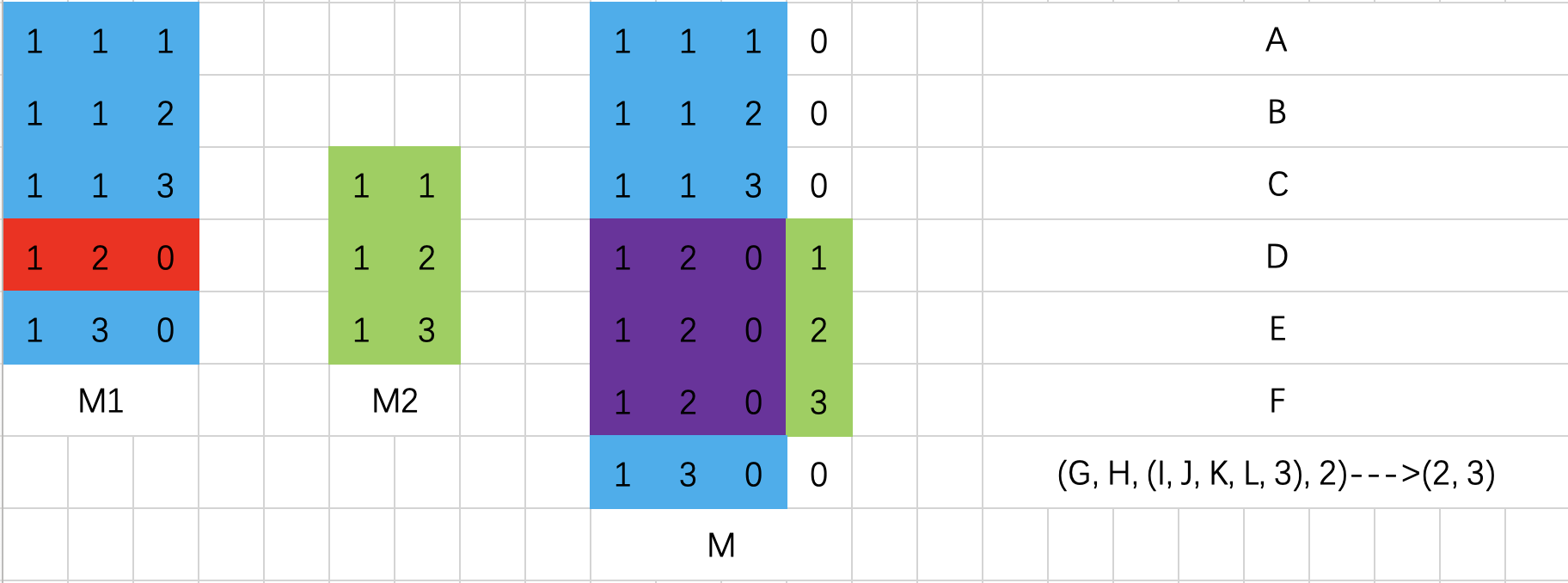
M1 中 红色部分为被替换的内容,M1 中被替换行的每个元素与 M2 中的第一列元素相乘为紫色部分,绿色为M2中剩余的部分。生成的结果M为下次递归计算的M1部分。
蓝色部分为 M1 中未被替换的内容,除去计算、保留的结果,矩阵中剩余的位置用 0 进行填充。