为啥要写数独题的题解
浅蓝色为考虑行/列/路径,深蓝色为考虑一个九宫格,绿色为考虑这一格
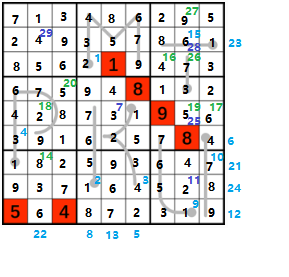
1:这个九宫格里已经有1了,路径上有7个点,由于如果路径上存在8,则会与下面的8同行,所以8不在路径上。
2:234已经出现在这一列,8已经出现在上方的九宫格,而且路径上最后一个格同行有9,因此路径为1567。
3:考虑除了路径上第二格以外的所在行,由于已经有6789,如果路径上有5则一定是在最后一格,但是这个九宫格里已经有5了,所以5不在路径上,因此路径为1234。
4:路径上最后一个点同行已经有8了,所以最后一个点为7或9。如果是7,则路径为1234567,此时2的同一行已经有2,所以不合法。因此最后一格为9。
考虑路径上是否有5,如果有5则不会出现在左侧的列上,也不能放在倒数第二格,则只能放在倒数第三格,但是此时路径前缀为12345,2同一行有2,则路径上不会有5。
又由于路径第二格不会是2,所以这时可以确定路径后6格为346789,第一格为1或2,不确定。
5:这一列只剩2格了,由于上面一格同行已经有2,所以2在下,5在上。
6:考虑这一行的7。左侧九宫格内已经有7,最右侧一格在长度为4的路径开头,不能是7,因此7在中间。然后最左侧九宫格内有4,因此4在最右侧,最左侧为1。
7:考虑九宫格中的4,九宫格正中间一格同行有4,左上一格同列有4,因此4在上方格子。左上格同行有3,因此3在正中。所以9就在左上了。
8:这一列就一格了,为8。
9:考虑路径倒数第二格,同行有5,所以只能是6或4。如果是4,路径为12347,2格同行已经有2,因此不合法,故倒数第二个为6。
2不会出现在路径上,第三格同行有4,也不能是3,则路径为13567。
10:56已经出现在九宫格了,因此路径为4789。
11:考虑九宫格里的4,不会在正中间,因此在上面格子,中间为2。
12:这一行就2格了,左边格子同列有7,因此7在右边,6在左边。
13:这一列也只有2格,上面格子同行有6,则6在下面,9在上面。
14:考虑这格所在的行,发现左边格子同行有8,右边格子只能是1或2,因此这格为8。
(Upd:其实这里就能直接推出一整行了,但是懒得重新画图了QwQ)
15:考虑路径第2格,23457都已经出现在同行或同列,路径最后一格同行又有9,因此这格只能为6,后一格为8。第一格暂时不确定。
16:这一格同行或同列只有4没出现过了。
17,18,19(又画复杂了QwQ):考虑该行,左侧和中间格子同列都有6,则6在最左侧。中间格同列有2,则2在左侧,5在中间。
20:九宫格中最后一格,为5。
21:右侧格子同列有1,因此1在左侧,2在右侧。
22:此列除从上往下第二格以外,同行都有4,则第2格为4,除第一格外同行都有1,则第1格为1,最下面一格同行有5,则第三格为5,最后一格为3。
23:这一行左,中同列都有1,则右侧格子为1,中间一格同列有2,则左侧为2,中间为9。
24:此行就剩2格,右侧格子同列有9,则左侧为9,右侧为7。
25:这个九宫格上方和右上格子同列都有1,则左上为1,中间同列有2,则右上为2,上方为3。
26:这格同行同列有除7以外的数,这格为7。
27:这一列唯一的一格,为9。
28:九宫格右侧一列有2,因此左上为2。右下同行有5,则右上为5,右下为3。
29:左侧一列有3,下侧一行有3,因此右上为3,左侧一列有6,则右下为6,下方一行有7,则左上为7,左下为8。