python内置数据结构和python列表

分类

数值型（int，float，complex，bool）

序列对象（字符串str，列表list，tuple）

键值对（集合set，字典dict）

数值型

int，float，complex，bool都是class，1,5.0,2+3j都是对象即实例。python3中的int就是长整型，且没有大小限制，受限于内存区域的大小。float有正数部分和小数部分组成。支持十进制和科学计数法表示，它只有双精度型。

complex有实数和虚数部分组成，实数和虚数部分都是浮点数3+4j。

bool是int类型的子类，仅有2个实例。True、False对应1和0，可以和整数直接运算。

类型转换（built——in）

int（x）返回一个正整数

float(x)返回一个浮点数

complx(x),complex(x,y)返回一个复数

bool(x)返回布尔值。

int(4.5)
bool(-10)

结果为4，True

数字的处理函数

import math
print(math.floor(2.5), math.floor(-2.5))
print(math.ceil(2.5), math.ceil(-2.5))

结果为：
2 -3
3 -2

print(int(-3.6), int(-2.5), int(-1.4))
print(int(3.6), int(2.5), int(1.4))
print(7//2, 7//-2, -7//2, -(7//2))
print(2//3, -2//3, -1//3)
print(round(2.5), round(2.5001), round(2.6))
print(round(3.5), round(3.5001), round(3.6), round(3.3))
print(round(-2.5), round(-2.5001), round(-2.6))
print(round(-3.5), round(-3.5001), round(-3.6), round(-3.3))

结果为：
-3 -2 -1
3 2 1
3 -4 -4 -3
0 -1 -1
2 3 3
4 4 4 3
-2 -3 -3
-4 -4 -4 -3

由上面的例子可以看到，round()函数是四舍六入五取偶。floor()是向下取整，ceil()是向上取整。int()取整数部分。//整除且向下取整。

其他的数字处理函数还有min(),max（），pow(x,y)等于x**y，math.sqrt()，进制函数（注意返回值是字符串）bin(),oct(),hex()。

math.pi是π。math.e是自然常数。

类型判断

type（obj），返回类型，而不是字符串。

isinstance(obj,class_or_tuple),返回布尔值。

a = 123
print(type(a))
print(type('abc'))
print(type(123))
print(isinstance(6, str))
print(isinstance(6, (str, bool, int)))

结果为：
<class 'int'>
<class 'str'>
<class 'int'>
False
True

print(type(1+True))
print(type(1+True+2.0)) 

结果为：
<class 'int'>
<class 'float'>

上面的例子可以看到，有隐式转换。

list

列表是python的基础数据类型之一，它是以[ ]括起来, 每个元素用逗号分隔开，且可以存放各种数据类型，任意对象，列表是有序的(按照你保存的顺序),有索引, 可以切片随便取值.。列表是可变的。

列表不能一开始就定义大小。

所以列表是一个队列，一个排列整齐的队伍，列表内的个体称为元素，列表是由若干个元素组成。同时元素可以是任意对象（可以是数字，字符串，对象，列表等），列表内的元素有顺序，可以使用索引。

列表是线性的数据结构，它是可变的。

列表list，链表，queen，stack的差异。

链表是手拉手。queen跟列表差不多，但是它可以先进先出，也可以先进后出，而stack可以想象成摞盘子的感觉。

list() -> new empty list
list(iterable) -> new list initialized from iterable's items
应该注意，列表不能一开始就定义大小。

a = list()
print(a)

结果为：
[]

a = []
print(a)

结果为：
[]

lst = [range(5)]
lst

结果为：
[range(0, 5)]

lst = list(range(5))
lst

结果为：
[0, 1, 2, 3, 4]

列表索引访问和修改

索引，也叫下标 ，从0开始，为列表中每一个元素编号 ，索引可以分为正索引和负索引，索引不可以超界，不然会引发异常。为了理解方便，可以认为列表是从左至右排列的，左边是头部，右边是尾部，左边是下界，右边是上界。

列表通过索引访问，list[index] ，index就是索引，使用中括号访问。

lst = ["ab", "cd", 1,2, 3]
print(lst[0]) # 获取第1个元素
print(lst[1])
print(lst[3])

结果为：
ab
cd
2

修改也通过索引修改。同时，应该注意的是，索引不要超界。

lst = ["ab", "cd", 1,2, 3]
lst[3] = 5
print(lst)


结果为：
['ab', 'cd', 1, 5, 3]

列表查询

index（value，[start,[stop]]）,这是通过值value，从指定区间查找列表内的元素是否匹配。匹配第一个就立即返回索引，匹配不到，抛出异常，valueerror。

count(value)是返回列表中匹配value的次数。

上面两个函数的时间复杂度都是O(N)，随着列表数据规模的增大，而效率下降。

而len()函数不是，这个在每次像列表中添加元素的时候就会计算。所以效率非常高，不再需要再遍历一次。

lst = list(range(5))
print(lst.index(3))
print(lst.count(0))
print(len(lst))

结果为：
3
1
5

查帮助可以查官方文档，同时可以help(keyword)，keyword可以是变量，对象，类名，函数名，方法名。

列表增加、插入元素

append(object)-->None

列表尾部追加元素，返回None，返回None就意味着没有新的列表产生，就地修改。它的时间复杂度是O(1)。

insert(index,object)-->None，这是在指定的索引index处插入元素object，返回None意味着没有新的列表元素产生，就地修改。它的时间复杂度是O(n)，它的索引可以超界，超越上界是尾部追加，而超越下界的话，则是尾部追加。

extend（iteratable）-->None,它是将可迭代对象的元素追加进来，返回None。它也是就地修改。

+ -->list,这是链接操作，将两个列表连接起来，这个操作会产生新的列表，原来的列表不变，本质上它是调用的__add__()方法。

* -->list，重复操作，本本列表元素重复N次，它也是返回新的列表。但是应该注意列表中的元素如果是引用，改变其中的一个元素，其他的元素也会改变。

x = [[1,2,3]]*3
print(x)
x[0][1] = 20
print(x)
y = [1]*5
y[0] = 6
y[1] = 7
print(y)

结果为：
[[1, 2, 3], [1, 2, 3], [1, 2, 3]]
[[1, 20, 3], [1, 20, 3], [1, 20, 3]]
[6, 7, 1, 1, 1]

列表删除元素

remove(value)-->None，这是从左到右查找第一个匹配value的值，然后移除该元素，返回None。这是就地修改。当然效率不高，时间复杂度是O（n）.

pop([index])-->item，这是不指定索引index，就从列表尾部弹出一个元素，指定索引index，就从索引处弹出一个元素，索引超界抛出indexerror错误，不指定索引效率很高，指定索引的话，效率很低。

clear()-->None，这是清除列表中的所有元素，剩下一个空列表。

列表其他操作

reverse（）-->None,这是将列表元素反转，返回None，这是就地修改。

reversed()是内置函数，它也是将列表反转，但是它会返回一个新的可迭代对象。

lst = [1,32,4,45,6,7,8]
lst.reverse()
print(lst)
a = reversed(lst)
print(lst)
print(a)
print(list(a))

结果为：
[8, 7, 6, 45, 4, 32, 1]
[8, 7, 6, 45, 4, 32, 1]
<list_reverseiterator object at 0x0000000005349708>
[1, 32, 4, 45, 6, 7, 8]

sort(key=None, reverse=False) -> None ，这是对列表元素进行排序，这是就地修改，默认是升序。reverse为True,反转，降序。key是一个函数，可以指定key如何排序。lst.sort(key = functionname)

sorted是对可迭代对象排序，返回一个新的对象。并不影响原来的对象。

列表复制

lst0 = list(range(4))
lst2 = list(range(4))
print(lst0==lst2)
lst1 = lst0#地址的引用。
lst1[2] = 10
print(lst0)
print(lst1)
print(lst2)

结果为：

True
[0, 1, 10, 3]
[0, 1, 10, 3]
[0, 1, 2, 3]

 

lst0 = list(range(4))
lst5 = lst0.copy()
print(lst5 == lst0)
lst5[2] = 10
print(lst5 == lst0)

True
False

copy()-->list,shadow copy,它返回一个新的列表。

lst0 = [1, [2, 3, 4], 5]
lst5 = lst0.copy()
print(lst5 == lst0)
lst5[2] = 10
print(lst5 == lst0)
lst5[2] = 5
lst5[1][1] = 20
print(lst5 == lst0)

结果为：
True
False
True

shadow copy，影子拷贝，也叫浅拷贝，遇到引用类型，只是复制了一个引用而已。

深拷贝，copy模块提供了deepcopy。

import copy
lst0 = [1, [2, 3, 4], 5]
lst5 = copy.deepcopy(lst0)
lst5[1][1] = 20
lst5 == lst0

结果为：
False

 

随机数

random模块，randint(a,b)返回[a,b]之间的整数。包括b。

choice(seq)从非空序列的元素中随机挑选一个元素，比如random.choice(range(10)),从0到9中随机挑选一个整数，random.choice([1,3,5,7])

randrange([start],stop,[step])从指定范围内，按指定基数递增的集合中获取一个随机数，基数缺省值为1，random.randrange(1,7,2)不包括7。

random.shuffle(list) ->None 就地打乱列表元素。

sample(population, k) 从样本空间或总体（序列或者集合类型）中随机取出k个不同的元素，返回一个新的列表。

import random
print(random.sample(['a', 'b', 'c', 'd'], 2))
print(random.sample(['a', 'a'], 2) )

结果为：
['d', 'c']
['a', 'a']

 列表练习

1，求100内的素数，从2开始到自身的-1的数中找到一个能整除的=》从2开始到自身开平方的数中找到一个能整除的。一个合数一定可以分解成几个素数的乘积，也就是说，一个数如果能被一个素数整除就是合数。

n = 100

lst = []
for i in range(3,n,2):#把偶数排除开

    for j in range(3,int(i**0.5 +1) ,2):#排除开偶数，因为奇数除以偶数没有意义
        if i%j==0:
            break
    else:
        print(i)#这里i就是质数

根据性质2，一个合数一定可以分解成几个素数的乘积。所以可以改造成下面这样：

n = 100

lst = [2]
for i in range(3,n,2):#把偶数排除开
    flag= True
    for j in lst:#lst是质数，如果j能被一个质数整除，那个这个数就是合数
        if j>i**0.5:
            flag = True
            break#是素数
        if i%j==0:
            flag = False
            break#合数
    if flag:
        print(i)#这里i就是质数
        lst.append(i)
print(lst)

#基本做法，一个数能被2开始到自己的平方根的正整数整数整除，就是合数。

import math
n = 100
lst = []
for x in range(2,n):
    for i in range(2,int(x**0.5 +1)):#math.ceil(math.sqrt(x)),为什么这样算出来不对？
        if x%i==0:
            break
    else:
        lst.append(x)
print(len(lst))

结果为：
25

#改进1，存储质数，合数一定可以分解为几个质数的乘积

import math
n = 100
lst = []
for x in range(2,n):
    for i in lst:
        if x%i==0:
            break
    else:
        lst.append(x)

print(len(lst))

结果为：
25

#改进2,使用质数存储已有的质数，同时增加范围

import math
n = 100
lst = []
for x in range(2,n):
    flag = False
    for i in lst:
        if x%i==0:
            flag = True
            break
        if i>math.ceil(math.sqrt(x)):
            break
    if not flag:
        lst.append(x)

print(len(lst))

我们来比较一下上面的效率

import datetime

upper_limit = 100000

start = datetime.datetime.now()
count = 1
for x in range(3,upper_limit,2):#舍弃掉所有偶数
    if x>10 and x%10==5:#所有大于10的质数中，个位数只有1,3,7,9.意思就是大于5，结尾是5就能被5整除了
        continue
    for i in range(3,int(x**0.5)+1,2):#为什么从3开始，且step为2.因为基数除以偶数没有意义
        if x%i==0:
            break
    else:
        count+=1
        #print(x,count)
        pass
delta = (datetime.datetime.now()-start).total_seconds()
print(delta)
print(count)
print('=====================')

#方法2
start = datetime.datetime.now()
x = 5
step = 2
count =2
#print(2,3,sep='
')
while x < upper_limit:
    for i in range(3,int(x**0.5)+1,2):#p和n都是奇数，那么不必和偶数整除
        if not x%i:
            break
    else:
        count+=1

    x+=step
    step =4 if step ==2 else 2
delta = (datetime.datetime.now()-start).total_seconds()
print(delta)
print(count)
print('+++++++++++++++++++++++++')

#方法3，使用列表存储已有的质数，同时增加范围
import math

start = datetime.datetime.now()
lst = []
count = 0
for x in range(2,upper_limit):
    flag = False
    for i in lst:
        if x%i==0:
            flag = True
            break
        if i>=math.ceil(math.sqrt(x)):
            flag = False
            break
    if not flag:
        count+=1
        lst.append(x)

delta = (datetime.datetime.now()-start).total_seconds()
print(delta)
print(count)
print('========================')

#方法4
start = datetime.datetime.now()
count = 2
for num in range(5,upper_limit):
    if num%6!=1 and num%6!=5:
        continue
    else:
        for i in range(5,int(num**0.5+1),2):
            if not num%i:
                break
        else:
            count+=1
delta = (datetime.datetime.now()-start).total_seconds()
print(delta)
print(count)

结果为：

0.2038
9592
=====================
0.171601
9592
+++++++++++++++++++++++++
0.549208
9592
========================
0.236013
9592

增加了列表并没有大幅度提升效率，为什么？

进一步修改。

start = datetime.datetime.now()
lst = []
count = 1
for x in range(3,upper_limit,2):#奇数
    flag = False
    for i in lst:
        if x%i==0:
            flag = True
            break
        if i>=math.ceil(math.sqrt(x)):
            flag = False
            break
    if not flag:
        count+=1
        lst.append(x)

delta = (datetime.datetime.now()-start).total_seconds()
print(delta)
print(count)
print('========================')

但是结果还是没有提高计算速度，为什么？

经过分析，得到下面的代码。

import datetime

upper_limit = 100000

start = datetime.datetime.now()
count = 1
for x in range(3,upper_limit,2):#舍弃掉所有偶数
    if x>10 and x%10==5:#所有大于10的质数中，个位数只有1,3,7,9.意思就是大于5，结尾是5就能被5整除了
        continue
    for i in range(3,int(x**0.5)+1,2):#为什么从3开始，且step为2.因为基数除以偶数没有意义
        if x%i==0:
            break
    else:
        count+=1
        #print(x,count)
        pass
delta = (datetime.datetime.now()-start).total_seconds()
print(delta)
print(count)
print('=====================')

#方法2
start = datetime.datetime.now()
x = 5
step = 2
count =2
#print(2,3,sep='
')
while x < upper_limit:
    for i in range(3,int(x**0.5)+1,2):#p和n都是奇数，那么不必和偶数整除
        if not x%i:
            break
    else:
        count+=1

    x+=step
    step =4 if step ==2 else 2
delta = (datetime.datetime.now()-start).total_seconds()
print(delta)
print(count)
print('+++++++++++++++++++++++++')

#方法3，使用列表存储已有的质数，同时增加范围
import math

start = datetime.datetime.now()
lst = []
count = 1
for x in range(3,upper_limit,2):#奇数
    edge = math.ceil(math.sqrt(x))
    flag = False
    for i in lst:
        if x%i==0:
            flag = True
            break
        if i>=edge:#math.ceil(math.sqrt(x))这个每次进来都要算一次，影响了效率。
            flag = False
            break
    if not flag:
        count+=1
        lst.append(x)

delta = (datetime.datetime.now()-start).total_seconds()
print(delta)
print(count)
print('========================')

#方法4
start = datetime.datetime.now()
count = 2
for num in range(5,upper_limit):
    if num%6!=1 and num%6!=5:
        continue
    else:
        for i in range(5,int(num**0.5+1),2):
            if not num%i:
                break
        else:
            count+=1
delta = (datetime.datetime.now()-start).total_seconds()
print(delta)
print(count)

直接提速，计算速度第一位，本质上就是空间换时间。

2.计算杨辉三角前6行，只求打印出杨辉三角的数字即可。（第N行有N项，第n项数字之和为2的N-1次方）

 

 

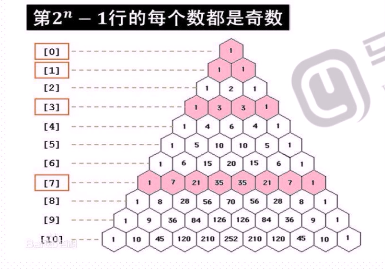
#基本实现，方法1，下一行依赖上一行所有元素，是上一行所有元素的两两相加的和，再在两头各加1.
triangle = [[1],[1,1]]

for i in range(2,6):
    cur = [1]#新行第一个元素
    pre = triangle[i-1]
    for j in range(len(pre)-1):
        cur.append(pre[j]+pre[j+1])
    cur.append(1)#内部尾巴
    triangle.append(cur)
print(triangle)

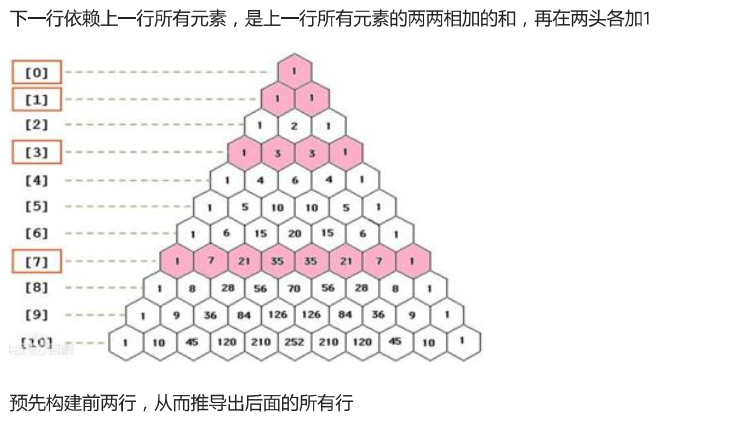
#变体，从第一行开始
triangle = []
n = 6

for i in range(n):
    cur = [1]
    triangle.append(cur)
    if i ==0:
        continue
    pre = triangle[i-1]
    for j in range(len(pre)-1):
        cur.append(pre[j]+pre[j+1])
    cur.append(1)
print(triangle)

结果为：
[[1], [1, 1], [1, 2, 1], [1, 3, 3, 1], [1, 4, 6, 4, 1], [1, 5, 10, 10, 5, 1]]

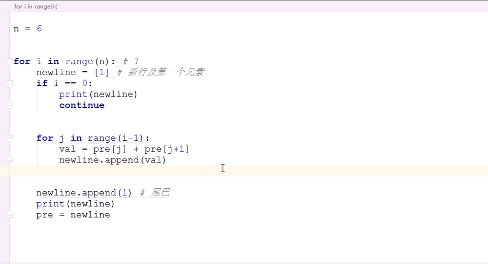
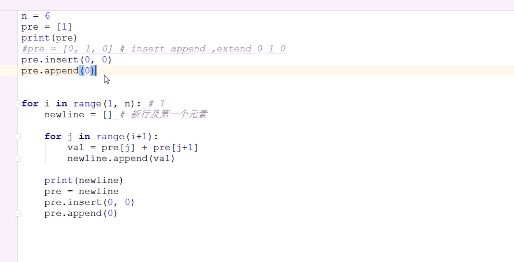
#补0，方法2，除了第一行外，每一行每一个元素（包括两头的1）都是由上一行的元素相加得到。
#如何得到两头的1,？目标是打印指定的行，所以算出一行就打印一行，不需要大空间存储所有已领算出的行。

#while循环实现
n = 6
newline = [1]#相当于计算好的第一行
print(newline)

for i in range(1,n):
    oldline = newline.copy()#浅拷贝并补0
    oldline.append(0)#尾部补0相当于两端补0
    newline.clear()#使用append，所以要清除

    offset= 0
    while offset<=i:
        newline.append(oldline[offset-1]+oldline[offset])
        offset+=1
    print(newline)

print("===================")
#for循环实现
n = 6
newline = [1]#相当于计算好的第一行
print(newline)

for i in range(1,n):
    oldline = newline.copy()  # 浅拷贝并补0
    oldline.append(0)  # 尾部补0相当于两端补0
    newline.clear()  # 使用append，所以要清除

    for j in range(i+1):
        newline.append(oldline[j-1]+oldline[j])
    print(newline)

 

 

 

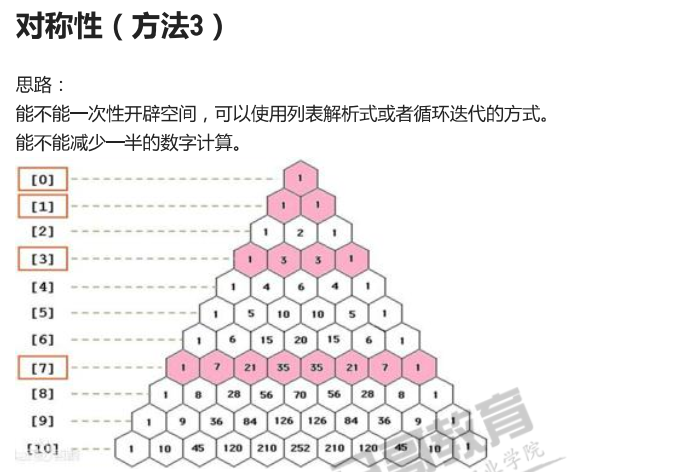
#方法3
triangle = []
n=6
for i in range(n):
    row = [1]#开始的1
    for k in range(i):#中间填0，尾部填1
        row.append(1) if k ==i-1 else row.append(0)
    triangle.append(row)
    if i==0:
        continue
    for j in range(1,i//2+1):#i=2第三行才能进来
        #print(i,j)
        val = triangle[i-1][j-1]+triangle[i-1][j]
        row[j] =val
        #i为2，j为0,1,2，循环一次
        #i为3，j为0,1,2,3，循环一次
        #i为4，j为0,1,2,3,4，循环2次
        if i!=2*j:#奇数个数的中点跳过
            row[-j-1]=val
print(triangle

 上面的代码看似不错，但行初始化的代码明显繁琐了，进一步简化。

triangle = []
n = 6
for i in range(n):
    row = [1]*(i+1)#一次性开辟
    triangle.append(row)
    for j in range(1,i//2+1):#i=2第三行才能进来
        #print(i,j)
        val = triangle[i-1][j-1] +triangle[i-1][j]
        row[j] = val
        if i!=2*j:#奇数个数的中点跳过
            row[-j-1] = val
print(triangle)

单行覆盖（方法4）

方法2每次都要清除列表，有点浪费时间。能够用上方法3的对称性的同时，只开辟一个列表实现吗？

 首先我们明确的知道所求最大行的元素个数，例如前6行的最大行元素个数为6个。

下一行等于首元素不变。覆盖中间元素。

n = 6
row = [1]*n #一次性开辟足够的空间

for i in range(n):
    offset = n-i
    z = 1#因为会有覆盖影响计算，所以引入一个临时变量
    for j in range(1,i//2+1):#对称性
        val = z+row[j]
        row[j],z = val,row[j]
        if i!=2*j:
            row[-j-offset] = val
    print(row[:i+1])

结果为：
[1]
[1, 1]
[1, 2, 1]
[1, 3, 3, 1]
[1, 4, 6, 4, 1]
[1, 5, 10, 10, 5, 1]

#基本实现，方法1，下一行依赖上一行所有元素，是上一行所有元素的两两相加的和，再在两头各加1.
triangle = [[1],[1,1]]

for i in range(2,6):
    cur = [1]
    pre = triangle[i-1]
    for j in range(len(pre)-1):
        cur.append(pre[j]+pre[j+1])
    cur.append(1)
    triangle.append(cur)
print(triangle)