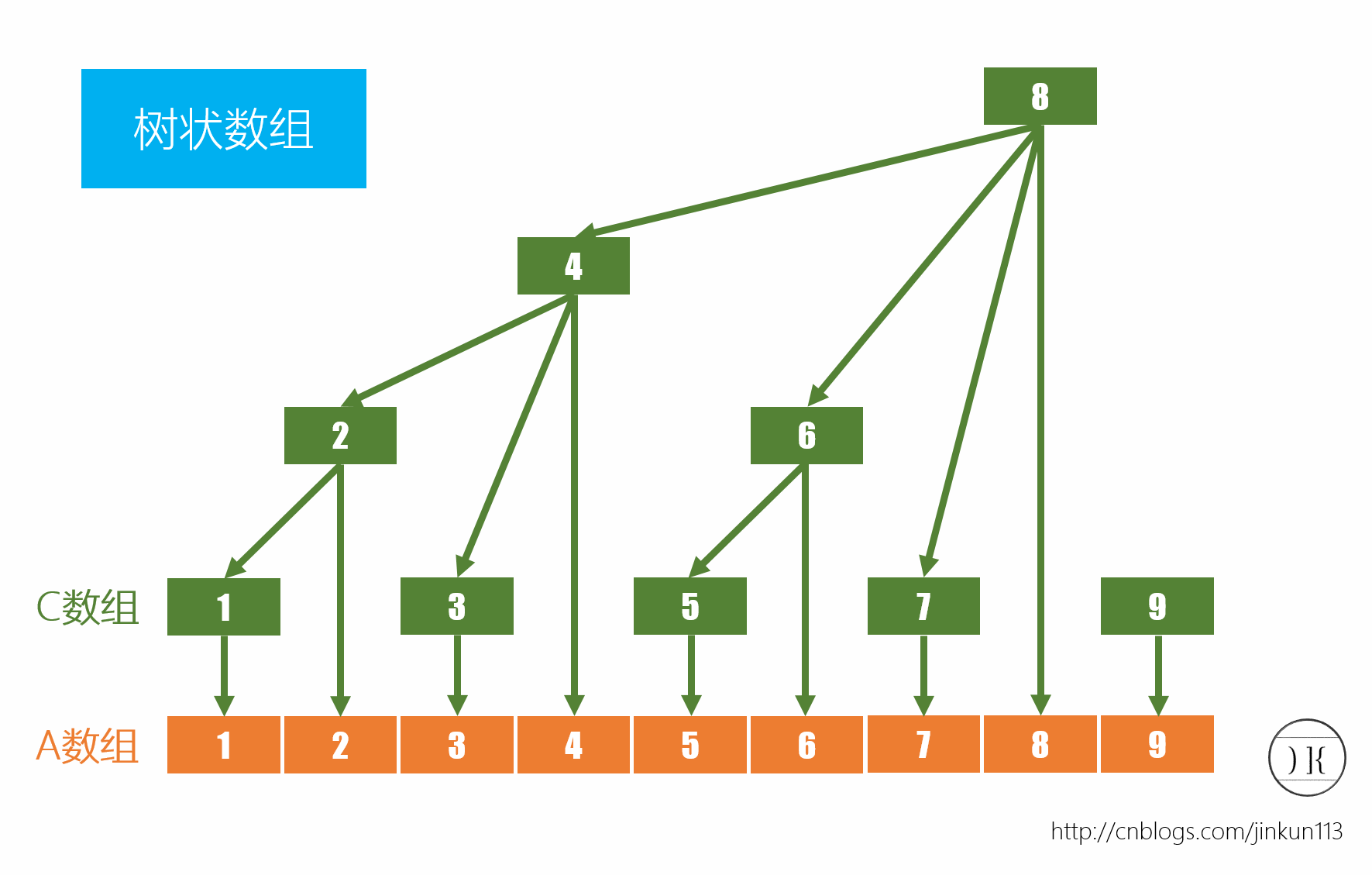
主要看图
i往上找就是i+=2^k; 往下就是减 k是i的二进制右边0的个数
2^k 直接等于i&(-i);
传送门:写的很好
总结
首先,明白树状数组所白了是按照二分对数组进行分组;维护和查询都是O(lgn)的复杂度,复杂度取决于最坏的情况,也是O(lgn);lowbit这里只是一个技巧,关键在于明白c数组的构成规律;分析的过程二进制一定要深入人心,当作心目中的十进制。
/*
树状数组
定义一个a数组一个c数组 记录和
c[i]=a[i-2^k+1]+...a[i] k位i的二进制右边0的个数
计算的时候计算a[1]+..a[r]-(a[1]+...a[l])的和 即为从l开始到r的和
用处有两个:
1.区间查询
2.单点更新
样例输入:
5
1 2 3 4 5 (数组元素)
2 4 (左区间和右区间)
输出:
9 (左右区间元素和)
*/
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<cstdio>
using namespace std;
int a[1000],c[1000];
int n;
int lowbit(int i){
return i&(-i);
}
//这样就可以直接算出2^k(k是2进制i中右边0的个数)
void change(int i,int x){
while(i<=n)//一直往上走 如 样例1->2->4->8 5->6->8
{
c[i]+=x;
i+=lowbit(i);
}
}
int getsum(int x){
int sum=0;
while(x>0){
sum+=c[x];
x-=lowbit(x);
}
return sum;
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
change(i,a[i]);
}
int l;int r;
scanf("%d%d",&l,&r);
//cout<<getsum(r)<<endl;
//cout<<getsum(l-1)<<endl;
cout<<getsum(r)-getsum(l-1)<<endl;
return 0;
}
更新元素计算
/*
树状数组 更新元素再求和
(更新数组中的元素 求左右区间内的元素和)
样例输入:
5
1 2 3 4 5 (数组元素)
2 4 (左区间和右区间)
1 (更新一组)
2 5(把二换成5)
输出:
12 (左右区间元素和)
*/
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<cstdio>
using namespace std;
int a[1000],c[1000];//一个a数组 一个c数组
int n;
int lowbit(int i){
return i&(-i);
}
//这样就可以直接算出2^k(k是2进制i中右边0的个数)
void change(int i,int x){
while(i<=n)
{
c[i]+=x;
i+=lowbit(i);
}
}
void deal(int i,int x){
int k=x-a[i];//差值
while(i<=n){
c[i]+=k;
i+=lowbit(i);
}
}
int getsum(int x){
int sum=0;
while(x>0){
sum+=c[x];
x-=lowbit(x);
}
return sum;
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);//一边读入一遍更新c数组
change(i,a[i]);
}
int l;int r;
scanf("%d%d",&l,&r);
int m;
scanf("%d",&m);//更新元素的组数
for(int i=1;i<=m;i++){
int p,q;//更新元素的位置和更新后的值
scanf("%d%d",&p,&q);
deal(p,q);
}
//cout<<getsum(r)<<endl;
//cout<<getsum(l-1)<<endl;
cout<<getsum(r)-getsum(l-1)<<endl;
return 0;
}
树状数组求逆序对
可见此网页
/*
样例
5
1 5 2 4 3
输出 4
*/
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<cstdio>
using namespace std;
int c[100010];
struct node{
int v,p;
}a[100010];
int n;
int lowbit(int i){
return i&(-i);
}
void update(int i){
while(i<=n)//一直往上走 如 样例1->2->4->8 5->6->8
{
c[i]++;
i+=lowbit(i);
}
}
int getsum(int x){
int sum=0;
while(x>0){
sum+=c[x];
x-=lowbit(x);
}
return sum;
}
bool cmp(node xx,node yy){
return xx.v<yy.v;
}
int main(){
scanf("%d",&n);
int ans=0;
for(int i=1;i<=n;i++){
scanf("%d",&a[i].v);
a[i].p=i;
}
sort(a+1,a+1+n,cmp);
//排序:离散化 如果a[i].v是10000000 那么c的内存就要到1000000 但是排序以后再找逆序对在内存和时间上更优
for(int i=1;i<=n;i++){
update(a[i].p);
ans+=i-getsum(a[i].p);
//cout<<i<<"-"<<getsum(a[i].p)<<"="<<ans<<endl;
}
cout<<ans;
return 0;
}