二叉树

二叉树是一种特殊的树，它的特点是每个结点最多有两个子树（即二叉树的度不能大于2），并且二叉树的子树有左右之分，其次序不能颠倒。

完美二叉树

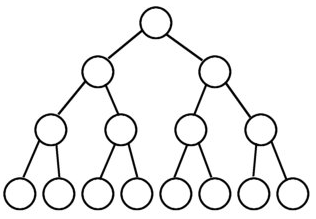
一棵深度为k 且有2^k -1 个结点的二叉树称为完美二叉树。

 

完全二叉树 

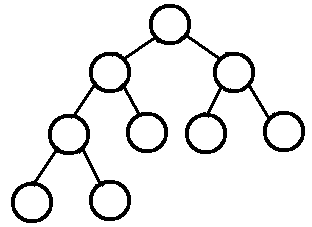
完全二叉树从root到 倒数第二层 之间形成是完美二叉树，而最后一层可以不是”满的“，也可以是”满的“，如果不是”满的“，则最后一层的结点必须靠左连续出现。

满二叉树

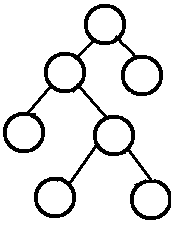
每一个结点要么度为0（是叶子结点），要么度为2（有2个孩子结点）。

遍历二叉树

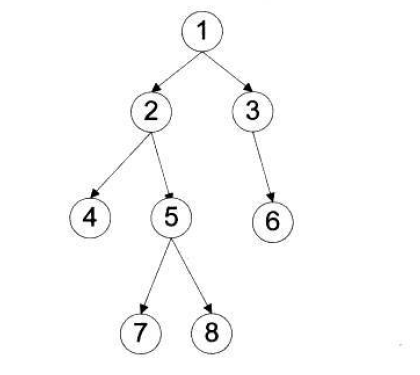
二叉树的遍历方式主要有：先序遍历、中序遍历、后序遍历、层次遍历。

 先序遍历：首先访问根结点然后遍历左子树，最后遍历右子树。在遍历左、右子树时，仍然先访问根结点，然后遍历左子树，最后遍历右子树，如果二叉树为空则返回。

1 2 4 5 7 8 3 6

中序遍历：中序遍历首先遍历左子树，然后访问根结点，最后遍历右子树。

4 2 7 5 8 1 3 6

后序遍历：后序遍历首先遍历左子树，然后遍历右子树，最后访问根结点，在遍历左、右子树时，仍然先遍历左子树，然后遍历右子树，最后遍历根结点。

4 7 8 5 2 6 3 1

层次遍历：1 2 3 4 5 6 7 8

例子一

将类似于'A(B(C(,),),E(,))'的字符串转化为二叉树结构

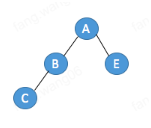
  var str = 'A(B(C(,),),E(,))';
  var node = new Node();
  var childNode;
  var reg1 = /w[(](S*)[)]/;
  var reg2 = /(w[(]S*[)])?(\,)(w[(]S*[)])?/;

  function Node(){
      this.data = '';
      this.left = null;
      this.right = null;
  }
  function build(str, node){
      if(apart(str)[0]){
          childNode = new Node();
          childNode.data = apart(str)[0].slice(0,1);
          node.left = childNode;
          build(apart(str)[0], childNode);
      }
      if(apart(str)[2]){
          childNode = new Node();
          childNode.data = apart(str)[2].slice(0,1);
          node.right = childNode;
          build(apart(str)[2], childNode);
      }
  }
  function apart(str){
      reg1.test(str);
      RegExp.$1;
      reg2.test(RegExp.$1);
      return [RegExp.$1, RegExp.$2, RegExp.$3];
  }
  node.data = str.slice(0,1);
  build(str, node);
  console.log(node);

输出：

例子二

  function Node() {        
    this.text = '';       
    this.leftChild = null;    
    this.rightild = null;    
  }
  var charecters = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z'];

  function buildBt1(node, i) {
    var leftIndex = 2*i+1,
      rightIndex = 2*i+2;            
    if(leftIndex < charecters.length) {       
      var childNode = new Node();       
      childNode.text = charecters[leftIndex];   
      node.leftChild = childNode;     
      buildBt1(childNode, leftIndex);    
    }
    if(rightIndex < charecters.length) {    
      var childNode = new Node();
      childNode.text = charecters[rightIndex];
      node.rightChild = childNode;
      buildBt1(childNode, rightIndex);
    }
  }

  var node = new Node();
  node.text = charecters[0];
  buildBt1(node, 0);
  console.log(node);

例子三

  function BinaryTree () {
    var Node = function (key) {
        this.key = key
        this.left = null
        this.right = null
    }
    var root = null
    this.rootNode = {}
    var insertNode = function (node,newNode) {
        if(newNode.key < node.key) {
            //左侧没有节点就插入
            if(node.left === null) {
                node.left = newNode
            }else {
                //递归比较进行插入
                insertNode(node.left,newNode)
            }
        }else {
            if(node.right === null) {
                node.right = newNode;
            }else {
                insertNode(node.right,newNode)
            }
        }
    }
    this.insert = function (key) {
        var newNode = new Node(key)
        if(root === null) {
            root = newNode
            this.rootNode = root
        }else {
            insertNode(root,newNode)
        }
    }
}
var nodesArr = [8,3,10,1,6,14,4,7,13]
var binaryTree = new BinaryTree();
nodesArr.forEach(key => binaryTree.insert(key))
console.log(binaryTree.rootNode)