【python-opencv】canny边缘检测

Canny Edge Detection是一种流行的边缘检测算法。它由John F. Canny发明，这是一个多阶段算法，我们将经历每个阶段。

1、降噪

由于边缘检测容易受到图像中噪声的影响，因此第一步是使用5x5高斯滤波器消除图像中的噪声。我们已经在前面的章节中看到了这一点。

2、查找图像的强度梯度

然后使用Sobel核在水平和垂直方向上对平滑的图像进行滤波，以在水平方向(Gx)和垂直方向(Gy)上获得一阶导数。从这两张图片中，我们可以找到每个像素的边缘渐变和方向。

渐变方向始终垂直于边缘。将其舍入为代表垂直，水平和两个对角线方向的四个角度之一。

3、非极大值抑制 在获得梯度大小和方向后，将对图像进行全面扫描，以去除可能不构成边缘的所有不需要的像素。为此，在每个像素处，检查像素是否是其在梯度方向上附近的局部最大值。查看下面的图片：

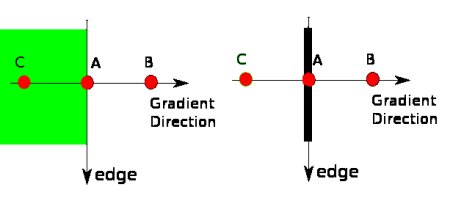
点A在边缘（垂直方向）上。渐变方向垂直于边缘。点B和C在梯度方向上。因此，将A点与B点和C点进行检查，看是否形成局部最大值。如果是这样，则考虑将其用于下一阶段，否则将其抑制（置为零）。 简而言之，你得到的结果是带有“细边”的二进制图像。 

4、磁滞阈值

该阶段确定哪些边缘全部是真正的边缘，哪些不是。为此，我们需要两个阈值minVal和maxVal。强度梯度大于maxVal的任何边缘必定是边缘，而小于minVal的那些边缘必定是非边缘，因此将其丢弃。介于这两个阈值之间的对象根据其连通性被分类为边缘或非边缘。如果将它们连接到“边缘”像素，则将它们视为边缘的一部分。否则，它们也将被丢弃，见下图：

边缘A在maxVal之上，因此被视为“确定边缘”。尽管边C低于maxVal，但它连接到边A，因此也被视为有效边，我们得到了完整的曲线。但是边缘B尽管在minVal之上并且与边缘C处于同一区域，但是它没有连接到任何“确保边缘”，因此被丢弃。因此，非常重要的一点是我们必须相应地选择minVal和maxVal以获得正确的结果。

opencv中的边缘检测：

OpenCV将以上所有内容放在单个函数cv.Canny()中。我们将看到如何使用它。第一个参数是我们的输入图像。第二个和第三个参数分别是我们的minVal和maxVal。第三个参数是perture_size。它是用于查找图像渐变的Sobel内核的大小。默认情况下为3。最后一个参数是L2gradient，它指定用于查找梯度幅度的方程式。如果为True，则使用上面提到的更精确的公式，否则使用以下函数：$Edge_Gradient ; (G) = |G_x| + |G_y|$。默认情况下，它为False。

import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt
img = cv.imread('dog2.jpg',0)
edges = cv.Canny(img,100,200)
plt.subplot(121),plt.imshow(img,cmap = 'gray')
plt.title('Original Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(edges,cmap = 'gray')
plt.title('Edge Image'), plt.xticks([]), plt.yticks([])
plt.show()

参考：http://woshicver.com/FifthSection/4_7_Canny%E8%BE%B9%E7%BC%98%E6%A3%80%E6%B5%8B/