这种类型问题三大要素:总重量、每件物品重量、每件物品价值,问最终能够塞进背包中的价值最大是多少?应该怎么选择物品?
当然也不一定是这些,例如上节所说的矿工挖矿:总人数、挖每座矿的人数、每座矿的金子数。
也就是说,只要出现了这三大要素,都可以视为0,1背包问题(物品不可拆分)
动态规划三要素:边界、最优子结构、状态转移方程。
我们一步步进行解析:
初始化:物品总重量:c=8,物品类别:n=['a','b','c','d'],物品重量:w=[2,4,5,3],物品价值:v=[5,4,6,2]
假设我们目前只有一个物品a,
- 背包的总重量为0,那么我们获得总价值为0
- 背包的总重量为1,那么我们获得总价值为1
- 背包的总重量为2,此时,正好可以放下物品a,因为它的重量正好是2,那么我们获得总价值为5
- 在这之后,我们可以获得的总价值均为5,因为总重量>2,且只有a一个物品
假设我们现在多了一个物品b,
- 背包总重量0,那么我们获得总价值为0
- 背包总重量1,那么我们获得总价值为0
- 背包总重量2,此时可以放进a,那么我们获得总价值为5
- 背包总重量3,仍只能放进a,那么我们获得总价值为5
- 背包总重量4,此时我们既可以放进a,也可以放进b,选价值最大的,也就是放进a,那么我们获得总价值为5
- 背包总重量5,那么我们获得总价值为5
- 背包总重量6,此时就可以放进a,b了,那么我们获得总价值为5+4=9
- 在这之后,我们可以获得的总价值均为9
假设我们现在多了一个物品c
- 背包总重量0,那么我们获得总价值为0
- 背包总重量1,那么我们获得总价值为0
- 背包总重量2,此时可以放进a,那么我们获得总价值为5
- 背包总重量3,仍只能放进a,那么我们获得总价值为5
- 背包总重量4,此时我们既可以放进a,也可以放进b,选价值最大的,也就是放进a,那么我们获得总价值为5
- 背包总重量5,此时我们可以放a,也可以放c,选最大的,也就是放进c,此时我们获得总价值为6
- 背包总重量6,此时可以放进a,b了,也可以只放进c,选最大的,那么我们获得总价值为5+4=9>6
- 在这之后,我们可以获得的总价值均为9

依此类推下去,看起来挺复杂,其实是有套路的,那我们应该如何实现。
对付这种问题,一般就直接初始化一个数组:dp[len(n)+1][c+1],即5行9列的二维数组(行代表物品种类,列代表总重量,多加一列和一行是为了更容易理解)
接下来,我们就从代码中一步步剖析:
n=['a','b','b','d'] c=8 w=[2,4,5,3] v=[5,4,6,2] def bag(c,w,v): #初始化数组,dp[i][j]表示总重量为j,物品种类为i,可以获得的最大价值 dp = [[0 for _ in range(c+1)] for _ in range(len(w)+1)] #定义边界,也就是当我们只有物品a,总重量依次由0-8 #也就是第一步我们所解释的 for i in range(1,c+1): if i>=w[0]: dp[1][i] = v[0] #遍历从第二行第一列开始 for i in range(2,len(w)+1): for j in range(1,c+1): #如果对于第i个物品,当前总重量放不下它,那么获得的最大值就是放下之前的i-1个 if j<w[i-1]: dp[i][j] = dp[i-1][j] #如果放得下,那么获得的最大值就是max(放下之前的i-1个,第i个物品的价值+ # (总重量-第i个物品的重量)在前i-1个物品的值) #注意下标,第i个物品的重量是w[i-1],价值是v[i-1] else: dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i-1]]+v[i-1]) return dp def show(c,w,dp): print("最大价值为:",dp[len(w)][c]) x = [False for _ in range(len(w)+1)] j = c #8 i = len(w) #4 while i>=0: if dp[i][j]>dp[i-1][j]: x[i]=True j=j-w[i-1] i-=1 print("选择的物品是:") for i in range(len(w)+1): if x[i]: print("第",i,"个",end='') print('') dp = bag(c,w,v) for i in range(len(w)+1): print(dp[i]) show(c,w,dp)
运行结果:
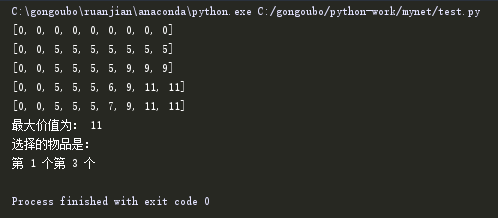
最后在输出第几个物品的时候采用由下往上,如果下面的值大于上面的值,说明这个物品被放置了,然后总重量减去该物品重量,继续判断,如蓝色所标记的。
总结:背包问题三步走:
(1)初始化dp数组,行为物品个数+1,列为总重量+1
(2)初始化边界,只放一个物品,在不同总重量下得到的价值
(3)遍历数组,依赖dp[i-1]更新dp[i]