P2467 [SDOI2010]地精部落
Description
Solution
神仙线性 \(dp\),然而还不会=-=
之前贺了一遍题解,现在又忘了,以后找机会再看看吧。
那么这里说一下 组合数 + \(dp\) 的方法:
设 \(dp_{i, 0/1}\) 表示长度为 \(i\) 且第一位为山峰/山谷的方案数,考虑如何转移。
我们枚举一个 \(j\),并假设第 \(j\) 位是最高的山峰,然后 \(1 \sim i\) 就被分成了 \(1 \sim j - 1\) 和 \(j + 1\sim i\),由于山峰山谷是交替的,所以我们可以根据 \(j\) 的奇偶性来判断第一位是山峰还是山谷从而决定更新 \(f_{i, 0}\) 还是 \(f_{i, 1}\)。
转移方程也比较好理解,假设第一位是 \(t \ (t = 0 或 1)\):
就是从 \(j\) 分开,根据乘法原理,两边的方案数相乘,这个组合数就是从剩下的 \(i - 1\) 个数中选择 \(j\) 个放到前面的方案数。
P2515 [HAOI2010]软件安装
Description
Solution
树上有依赖背包板子题,不过要先缩个点。
而且此题 \(O(n^3)\) 可过,不需要 dfs 序优化等方式进行优化。
dfs 里这样转移一下即可:
for(auto y : g[x]){
dfs(y);
for(int i = m; i >= wei[x]; --i)
for(int j = 0; j <= i - wei[x]; ++j)
dp[x][i] = max(dp[x][i], dp[y][j] + dp[x][i - j]);
}
P4822 [BJWC2012]冻结
Description
Solution
分层图最短路板子题,如果有不会的话,可以去看一下我博客里的 P4568 飞行路线(我一直以为这是板子,好吧其实差不多)的 题解。
P2303 [SDOI2012] Longge 的问题
Description
Solution
看到 \(gcd\) 这个东西,有个非常套路的转化,以本题为例:
我们改为枚举一个 \(d\),求 \(gcd(i, n) = d\) 的个数然后乘起来,写成式子就是:
然后右边这个 \(gcd(i, n) = d\) 又有一个很明显的转化:
所以答案就是:
P1955 [NOI2015] 程序自动分析
Description
Solution
第一眼以为是 2-sat 之类的,感觉这么难不应该绿吧。
然后看了一眼标签,发现,并查集……
那么这题就很水了,排个序,去重然后一个一个扔到并查集里就完了。
P4208 [JSOI2008]最小生成树计数
Descruption
Solution
表示并不会矩阵树定理……
然后去看了第一篇题解,暴力大法吼啊!
一个结论:
不管最小生成树怎么变,权值相同的边的个数是固定的。
然后就先一发 \(Kruskal\) 整个最小生成树出来,然后记录一下边,计算个数的时候爆搜一下权值相同的边,用乘法原理乘一下就完了。
注意:\(Kruskal\) 时不能路径压缩,不然 dfs 的时候就会乱。
P4105 [HEOI2014]南园满地堆轻絮
Description
Solution
高质量河北省省选题。
先二分一下最小值最大是多少,假设当前二分为 \(mid\)。
明显第一个数直接减去 \(mid\) 最优,然后依次判断 \(2 \sim n\)。
遇到一个数能减就减,如果减去 \(mid\) 之后依然大于前一个数,返回不行,调大 \(mid\)。
P3225 [HNOI2012]矿场搭建
Description
Solution
先用 \(Tarjan\) 找到所有割点,然后 dfs 一遍找到每一组点(由割点分割而成的不同组),一下我们按一个联通块讨论:
- 没有割点:需要建两个,如果有一个救援出口塌了还可以走另一个,
- 有一个割点:只需要建一个出口即可,且出口不在割点上。
- 有两个或以上割点:不需要建出口,可以直接到达其他组。
方案数用乘法原理乘一下即可。
有趣的家庭菜园
Solution
按高度从大到小排序,依次插入每一株草,每次查询一下当前草左右比它高的草的个数有多少,取较少值加到答案里。
树状数组维护一下,注意,相同高度也合法,所以对于相同高度的要先统计所有答案,再更新。
P3625 [APIO2009]采油区域
Descrption
Solution
神仙 \(dp\)。
很巧妙的一种思想:分类讨论
分为 6 种情况,如下图:
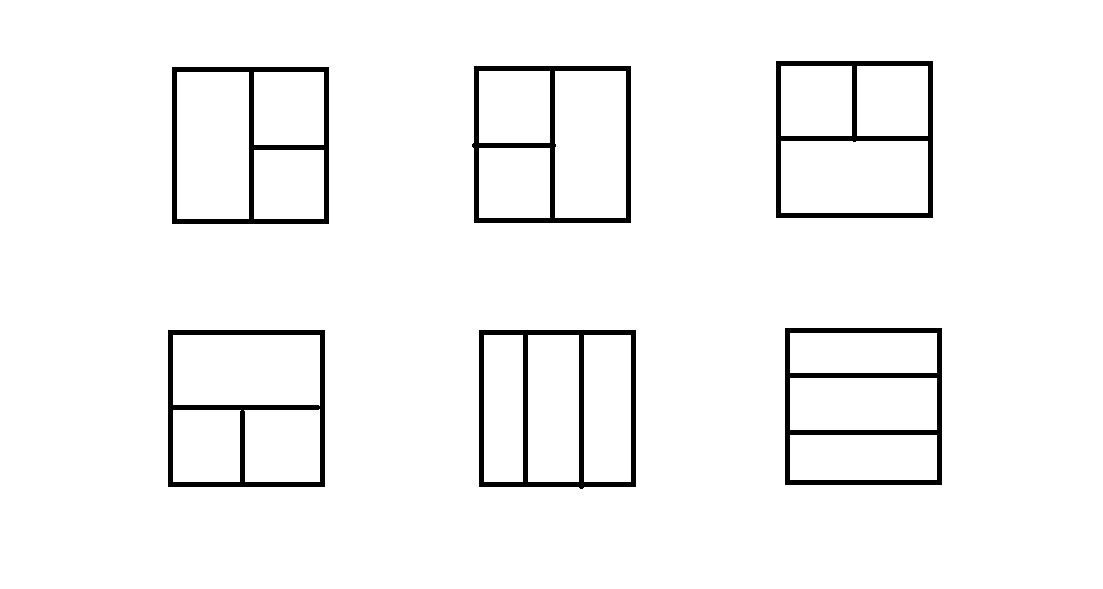
可以发现,每一张图都被分为了 3 块,我们就可以分别在这三个部分中各选择一个 \(k * k\) 的矩形,取最大值。
具体实现:
首先要进行预处理,设一个点为 \((x, y)\)
我们要预处理出以这个点为端点向左上,右上,左下,右下,四个方向分别的最大子矩阵。
然后我们枚举上图中每个矩形中的那两条线,再取最大值即可。
具体看代码吧。
P4053 [JSOI2007]建筑抢修
Description
Solution
反悔贪心经典题。
错误的贪心:先选截止时间靠前的,错误性显然。
我们还是要先按截止时间排序。
开一个大根堆,记录贪心选中的建筑所需的修理时间,显然堆顶是最劣解,即所需的修理时间最长。
考虑插入每一个建筑的过程(\(tim\) 是当前所用的时间):
- \(tim + T1_i \leq T2_i\):直接放到堆中,且 \(tim += T1_i\)。
- \(tim + T1_i > T2_i\):判断 \(T2_i\) 与堆顶元素的大小,并决定是否替换。
证明:
显然修理相同数量的建筑的情况下,所用的修理时间越少越好。
我们判断当前建筑所需的修理时间和堆顶元素的大小并决定是否替换就是为了满足这个贪心性质。
详见博客浅谈反悔贪心 - xixike
P4052 [JSOI2007]文本生成器
Description
Solution
AC 自动机上 \(dp\)。
首先给单词们建一个 \(AC\) 自动机。
计算可读文本的数量有些困难,考虑正难则反,用总数减去不可读的文本数量。
不可读的数量即为跑不到单词结尾的文本数量。
我们设 \(f_{i, j}\) 表示到长度 \(i\) 当前在节点 \(j\) 的不可读文本数量。
那么转移就是:
答案就是:\(ans = 26^m - \sum\limits_{i = 0}^{tot}f_{m, i}\)
P2319 [HNOI2006]超级英雄
Description
Solution
类似于连续攻击游戏,还是二分图匹配。
我们发现一个“锦囊妙计”对应两道题目,且只能使用一次。
我们把问题和”锦囊妙计“之间连边,从 1 枚举匹配一下,如果有无法匹配的直接break。
P1772 [ZJOI2006]物流运输
Description
Solution
设 \(dp_{i}\) 表示前 \(i\) 天最小的成本。
转移方程:\(dp_{i} = min\{dp_{j} + cost_{j + 1, i} * (i - j) + k \}\)
就是从 \(j + 1 \sim i\) 天都走同一条路,但与第 \(j\) 天不同。
\(cost_{i,j}\) 如何计算呢?
我们把 \(i \sim j\) 天封闭的码头都设为不可走,然后跑一遍最短路即可。