一、线性回归问题
1、线性回归问题介绍
(1)示例介绍
数据:工资和年龄(2个特征)
目标:预测银行会贷款多少钱(标签)
考虑:工资和年龄都会影响最终银行贷款的结果,那么它们各自有多大的影响?(参数)
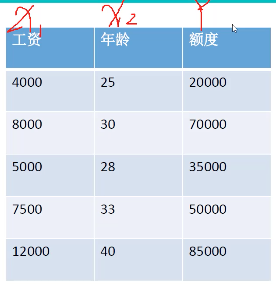
通过图表可以看出随着工资和年龄的增长,贷款额度也随之增长。X1和X2的数量级是不同的,因此需要增加两个因子:θ1x1+θ2x2=y ,在已知x1,x2,y的情况下建立回归方程。方程的目标就是求出最合适的θ1、θ2,这样就知道工资和年龄对贷款额度到底有多大的影响。
(2)通俗解释
X1、X2就是我们的两个特征(年龄、工资),Y是银行最终会借给我们多少钱。
找到最合适的一条线(想象一个高维)来最好的拟合我们的数据点。(无法满足所有,满足尽可能多的点)
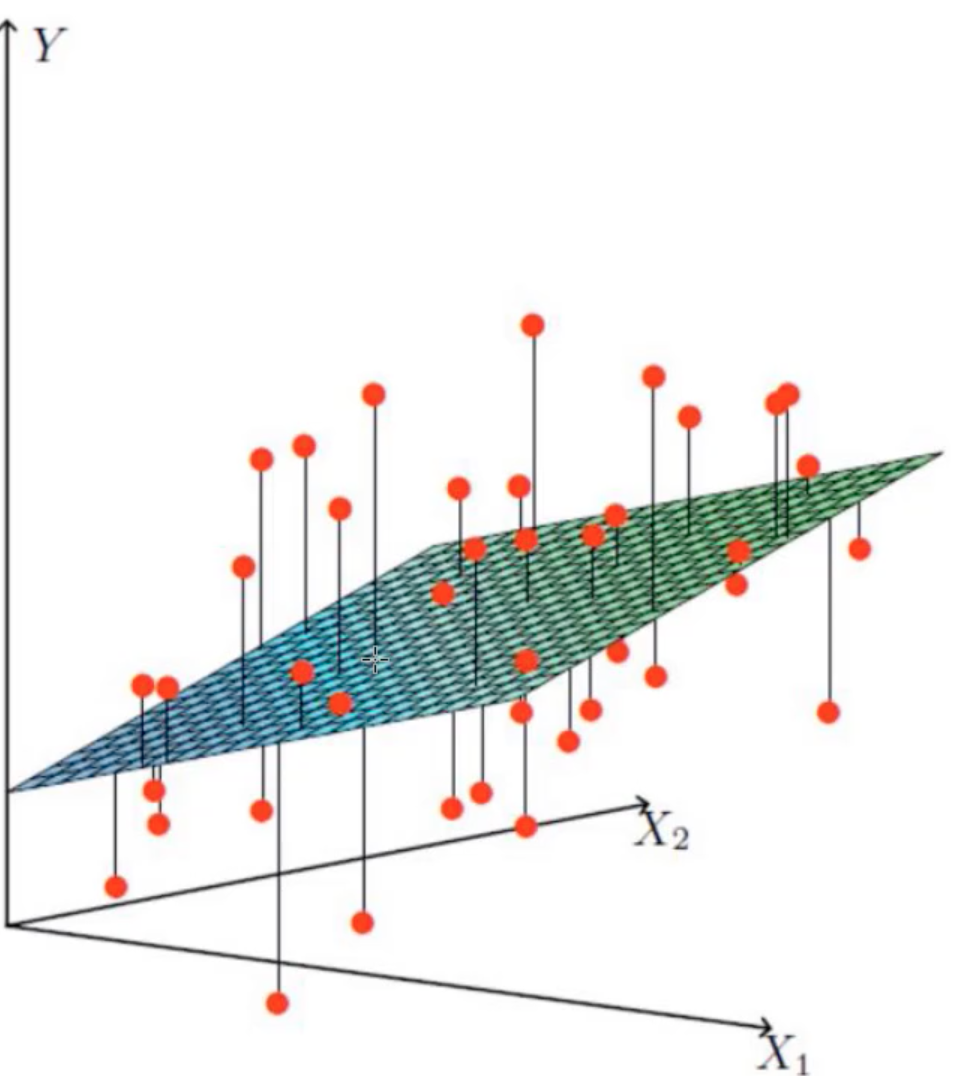
图中红点是样本数据,想根据给定的数据集拟合一个平面,使得各个样本数据到达平面的误差最小。
这个图就是机器如何进行预测的(回归)它会根据贷款的历史数据(年龄和工资分别对应于X1与X2)找出来最好的拟合线(面)来进行预测,这样新的数据来了之后直接带入进去就可以得出来该给多少钱了。
(3)进一步整合回归方程
整合是把偏置项和权重参数项放到了一起(加了个θ0让其都等于1)。
- 假设θ1是年龄的参数,θ2是工资的参数。
- 拟合的平面:hθ(x) = θ0 + θ1x1 + θ2x2 。参数θ1、θ2为权重项,对结果影响较大。θ0是偏置项。
- 整合:
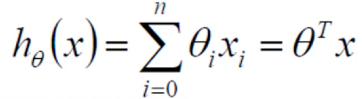
2、偏置项理解
一个传统的神经网络就可以看成多个逻辑回归模型的输出作为另一个逻辑回归模型的输入的“组合模型”。
因此,讨论神经网络中的偏置项b的作用,就近似等价于讨论逻辑回归模型中的偏置项b的作用。
(1)逻辑回归偏置项
逻辑回归模型本质:利用 y = WX + b 这个函数画决策面,其中W为模型参数,也是函数的斜率;b为函数的截距。
一维情况:W=[1],b=2,y=WX+b得到一个截距为2,斜率为1的直线如下所示:
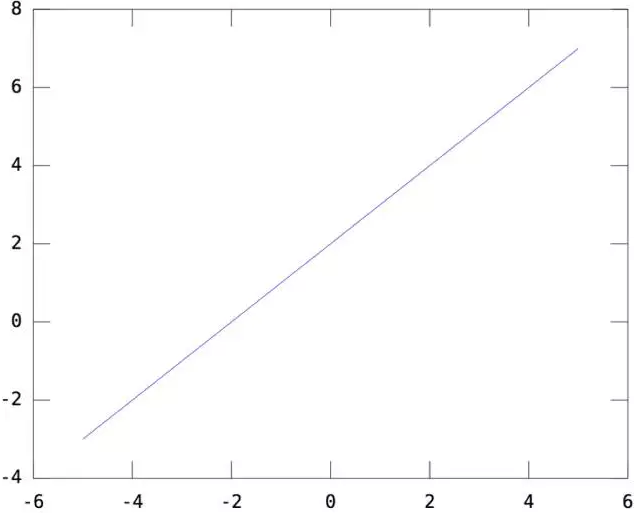
二维情况:W=[1 1],b=2,则 y=WX+b得到一个截距为2,斜率为[1 1]的平面如下所示:
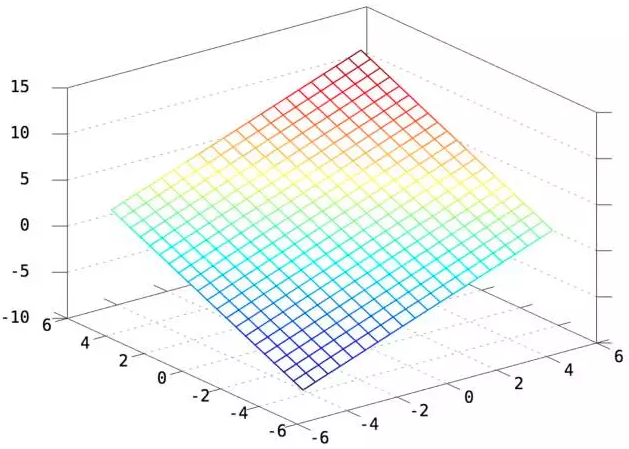
显然y=WX+b这个函数,就是2维/3维/更高维空间的直线/平面/超平面。如果没有偏置项b,则只能在空间里画过原点的直线/平面/超平面。
因此对于逻辑回归必须加上偏置项b,才能保证分类器可以在空间任何位置画决策面。
(2)神经网络偏置项
同理,对于多个逻辑回归组成的神经网络,更要加上偏置项b。
如果隐层有3个节点,那就相当于有3个逻辑回归分类器。这三个分类器各画各的决策面,那一般情况下它们的偏置项b也会各不相同。
复杂决策边界由三个隐层节点的神经网络画出如下:
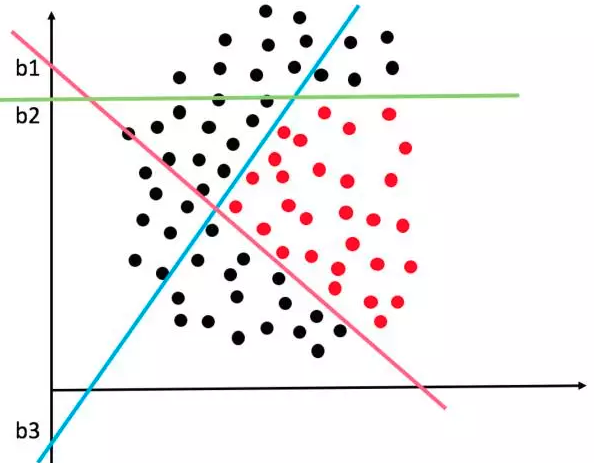
如何机智的为三个分类器(隐节点)分配不同的b呢?或者说如果让模型在训练的过程中,动态的调整三个分类器的b以画出各自最佳的决策面呢?
那就是先在X的前面加个1,作为偏置项的基底,(此时X就从n维向量变成了n+1维向量,即变成 [1, x1,x2…] ),然后,让每个分类器去训练自己的偏置项权重,所以每个分类器的权重就也变成了n+1维,即[w0,w1,…],其中,w0就是偏置项的权重,所以1*w0就是本分类器的偏置/截距啦。这样,就让截距b这个看似与斜率W不同的参数,都统一到了一个框架下,使得模型在训练的过程中不断调整参数w0,从而达到调整b的目的。
所以,如果在写神经网络的代码的时候,把偏置项给漏掉了,那么神经网络很有可能变得很差,收敛很慢而且精度差,甚至可能陷入“僵死”状态无法收敛。
3、误差项定义
银行的目标得让误差越小越好,这样才能够使得我们的结果是越准确的。
- 真实值和预测值之间肯定要存在差异——用 ε 来表示该误差。
- 对于每个样本:y(i) = θTx(i) + ε(i) ,y(i)是真实值,θTx(i)是预测值, ε(i)是差异值。
- 每一个样本的误差值是不同的:

4、误差规律——独立同分布
独立同分布(iid,independently identically distribution)在概率统计理论中,指随机过程中,任何时刻的取值都为随机变量,如果这些随机变量服从同一分布,并且互相独立,那么这些随机变量是独立同分布。
- 误差ε(i)是独立且具有相同分布,并且服从均值为0方差为θ2的高斯分布;
- 独立:张三和李四一起来贷款,他俩没有关系,即每个样本到拟合平面的距离都不相同;
- 同分布:他俩都来得是我们假定的同一家银行,所以它在预测的时候是按照同样的方式,数据是在同一个分布下去建模,尽可能来自相同的分布;
- 高斯分布:银行可能会多给,也可能会少给,但是绝大多数情况下,这个浮动不会太大,极小情况下浮动会比较大(有的多有的少,大概来看,均值为0)。

误差在0附近浮动的可能性较大,正负差距较大的可能性越来越小。符合概率统计中现实分布情况。
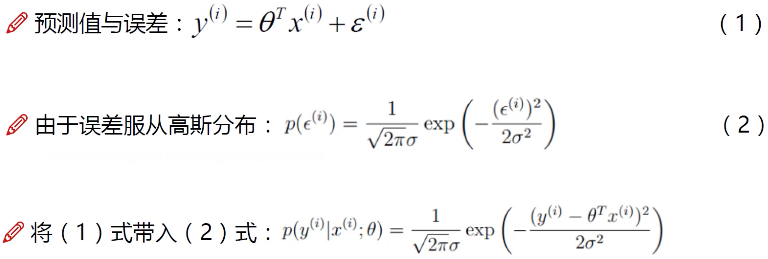
将(1)式转化为:ε(i) = y(i) - θTx(i) ,即:误差=实际值-预测值,然后带入高斯分布函数(2)式,就将误差项都替换为了x,y。
p(x;θ)代表:在给定θ的情况下x的取值;
p(y|x;θ)代表:在给定x的情况下,还给定某种参数θ的情况下,y的概率密度函数。
由于x和θ是一个定值,所以θTx(i) 可以理解为一个定值C。
5、似然函数
似然函数是一种关于模型中参数的函数,用来表示模型参数中的似然性。
已知样本数据x(x1,x2,...,xn)组合,要使用什么样的参数θ和样本数据组合后,可以恰好得到真实值?
要让误差项越小越好,则要让似然函数越大越好,由此将问题转为求L(θ)的最大值。
(1)引入似然函数
引入似然函数如下:(Π从...到...的积)
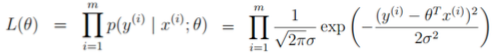
连续型变量相互独立的充要条件是联合概率密度等于边缘概率密度的乘积。因此变量符合独立同分布前提下,联合概率密度等于边缘概率密度的乘积成立。
p(y(i) | x(i);θ):什么样的x和θ组合完后,能成为y的可能性越大越好。m项的乘积非常难解,难以估计,因此要想办法转为加法。
对数似然:乘法难解,加法相对容易,对数里面乘法可以转换成加法,因此对式子左右两边取对数。
log(AB) = logA + logB
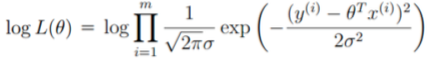
(2)为什么取对数?
首先,取对数不影响函数的单调性,保证输入对应的概率的最大最小值对应似然函数的最值。
其次,减少计算量,比如联合概率的连乘会变成加法问题,指数亦可。
最后,概率的连乘将会变成一个很小的值,可能会引起浮点数下溢,尤其是当数据集很大的时候,联合概率会趋向于0,非常不利于之后的计算。依据ln曲线可知,很小的概率(越接近0)经过对数转换会转变为较大的负数,解决下溢问题。
取对数虽然会改变极值,但不会改变极值点。任务依然是求极值,因此L(θ)和logL(θ)两者是等价的。
6、参数求解
(1)公式继续展开化简
继续处理: 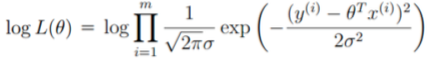 ,由于log A·B = logA + logB,因此可以将累乘转换为累加:
,由于log A·B = logA + logB,因此可以将累乘转换为累加: 。
。
进一步观察发现,可以将上面的式子看作是 和
和 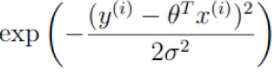 两部分的组合,即log A·B = logA + logB。
两部分的组合,即log A·B = logA + logB。
这里要求解是的 θ,因此其他的都可以看作是常数项。 因此可以把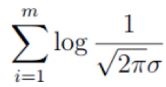 看作是m倍的常数项:
看作是m倍的常数项: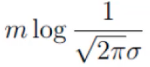 。
。
再观察另一个部分: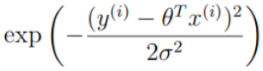 ,exp:高等数学里以自然常数e为底的指数函数,它同时又是航模名词,全称Exponential(指数曲线)。由于给对数取不同的底数只会影响极值,但不会影响极值点。
,exp:高等数学里以自然常数e为底的指数函数,它同时又是航模名词,全称Exponential(指数曲线)。由于给对数取不同的底数只会影响极值,但不会影响极值点。
将这一部分底数取e,则与exp(x)的以e为底的指数发生抵消,再将常数项提取出来,可以将公司转成这种累加形式: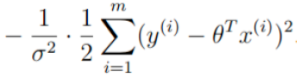
公式到这里就不能继续化简了,毕竟每个人的年龄(x)和每个有多少钱(y)是不同的,因此,必须从第一个样本迭代到第m个样本。最终简化为:
(2)目标:让似然函数越大越好
之前的目标:x和θ组合完后,成为y的可能性越大越好。因此现在要求得极大值点。A是一个恒为正的常数,B中包含平分因此也是一个正数。因此是两个正数间的减法。
如要求值越大越好,因此B: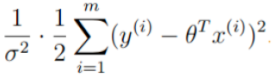 必须越小越好。
必须越小越好。
现在就将目标转换为求解最小二乘法。
二、求解最小二乘法
从上面的推导可以得出结论:要求让似然函数越大越好,可转化为求θ取某个值时使J(θ)最小的问题。
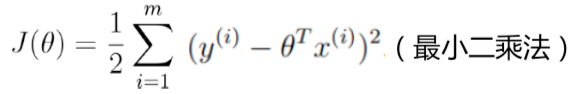
求解最小二乘法的方法一般为两种:矩阵式、梯度下降法。
1、矩阵式求解
数据集含有m个样本,每个样本有n个特征时:
- 数据x可以写成m*(n+1)维的矩阵(+1是添加一列1,用于与截断b相乘);
- θ则为n+1维的列向量(+1是截断b);
- y为m维的列向量代表每m个样本结果的预测值。
矩阵式的推导如下所示:
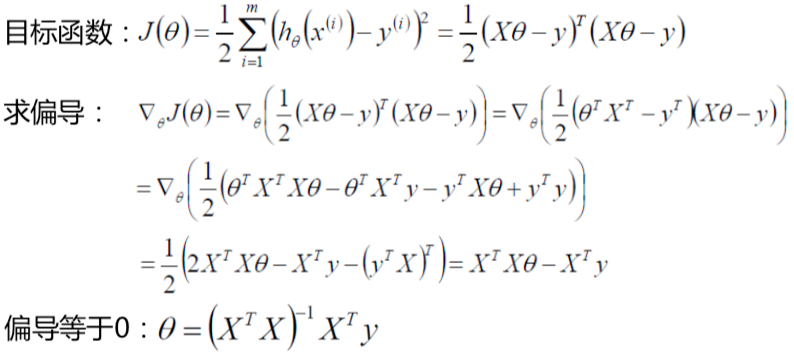
让J(θ)对θ求偏导,当偏导等于零时,则这个θ就是极值点。XT代表X矩阵的转置,XT与X的乘积一定会得到一个对称阵。
另外存在公式: θTXTXθ 等于 2XTXθ。
XTX的逆矩阵为:(XTX)-1 ,将这个逆矩阵分别乘到偏导结果等式两边,左边期望是零,推导得到:
0 = θ - (XTX)-1 · XTy,转换等式得到:θ=(XTX)-1XTy
这种方法存在的问题:不存在学习的过程;矩阵求逆不是一个必然成功的行为(存在不可逆);
2、梯度下降法(GD)
目标函数: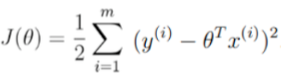
对于多元线性回归来说,拟合函数为: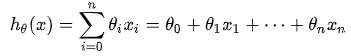
由于目标函数是由m个样本累加得到的,因此可以求一个平均得到损失函数: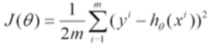
1)对损失函数求偏导数,批量梯度下降:
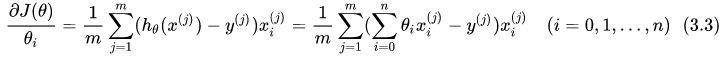
容易得到最优解,但是每次考虑所有样本,执行速度很慢。
2)每次只用一个样本,随机梯度下降:
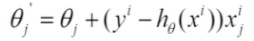
去除累加操作,每次抽样一个样本来计算,速度快,结果不准。
3)每次更新选择一部分数据,小批量梯度下降法:
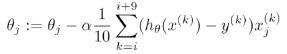
(1)为什么要使用梯度下降
当得到一个目标函数时,通常是不能直接求解的,线性回归能求出结果在机器学习中是一个特例。
机器学习常规套路:交给机器一堆数据,然后告诉它使用什么样的学习方式(目标函数),然后它朝着这个方向去学习。
算法优化:一步步完成迭代,每次优化一点点,积累起来就能获得大成功。
(2)梯度概念
在一元函数中叫做求导,在多元函数中就叫做求梯度。梯度下降是一个最优化算法,通俗的来讲也就是沿着梯度下降的方向来求出一个函数的极小值。比如一元函数中,加速度减少的方向,总会找到一个点使速度达到最小。
通常情况下,数据不可能完全符合我们的要求,所以很难用矩阵去求解,所以机器学习就应该用学习的方法,因此我们采用梯度下降,不断迭代,沿着梯度下降的方向来移动,求出极小值。
梯度下降法包括批量梯度下降法和随机梯度下降法(SGD)以及二者的结合mini批量下降法(通常与SGD认为是同一种,常用于深度学习中)。
(3)梯度下降法实验
对于梯度下降,我们可以形象地理解为一个人下山的过程。假设现在有一个人在山上,现在他想要走下山,但是他不知道山底在哪个方向,怎么办呢?显然我们可以想到的是,一定要沿着山高度下降的地方走,不然就不是下山而是上山了。山高度下降的方向有很多,选哪个方向呢?这个人比较有冒险精神,他选择最陡峭的方向,即山高度下降最快的方向。现在确定了方向,就要开始下山了。
又有一个问题来了,在下山的过程中,最开始选定的方向并不总是高度下降最快的地方。这个人比较聪明,他每次都选定一段距离,每走一段距离之后,就重新确定当前所在位置的高度下降最快的地方。这样,这个人每次下山的方向都可以近似看作是每个距离段内高度下降最快的地方。
现在我们将这个思想引入线性回归,在线性回归中,我们要找到参数矩阵 使得损失函数
最小。如果把损失函数
看作是这座山,山底不就是损失函数最小的地方吗,那我们求解参数矩阵
的过程,就是人走到山底的过程。
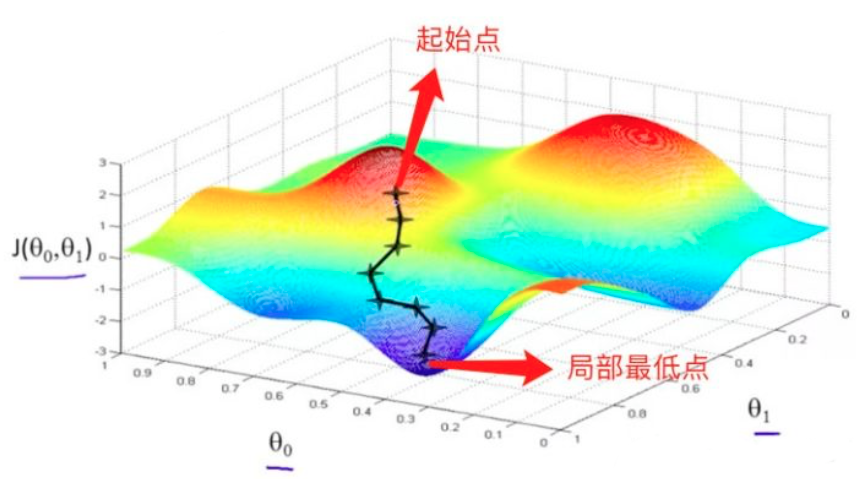
如图所示,这是一元线性回归(即假设函数 )中的损失函数图像,一开始我们选定一个起始点(通常是
),然后沿着这个起始点开始,沿着这一点处损失函数下降最快的方向(即该点的梯度负方向)走一小步,走完一步之后,到达第二个点,然后我们又沿着第二个点的梯度负方向走一小步,到达第三个点,以此类推,直到我们到底局部最低点。为什么是局部最低点呢?因为我们到达的这个点的梯度为 0 向量(通常是和 0 向量相差在某一个可接受的范围内),这说明这个点是损失函数的极小值点,并不一定是最小值点。

从梯度下降法的思想,我们可以看到,最后得到的局部最低点与我们选定的起始点有关。通常情况下,如果起始点不同,最后得到的局部最低点也会不一样。
(4)参数更新
每次更新参数的操作:

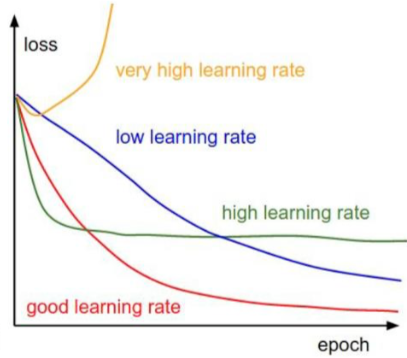
其中α为学习率(步长),对结果会产生巨大的影响,调节学习率这个超参数是建模中的重要内容。
选择方法:从小的开始,不行再小。
批处理数量:32、64、128比较常用,很多时候还要考虑内存和效率。
因为J(θ)是凸函数,所以GD求出的最优解是全局最优解。批量梯度下降法是求出整个数据集的梯度,再去更新θ,所以每次迭代都是在求全局最优解。
三、单特征回归建模
1、数据预处理
写一个prepare_for_training函数,对数据进行函数变换、标准化等操作。最后返回处理过的数据,以及均值和标准差。
import numpy as np from .normalize import normalize from .generate_sinusoids import generate_sinusoids from .generate_polynomials import generate_polynomials """数据预处理""" def prepare_for_training(data, polynomial_degree=0, sinusoid_degree=0, normalize_data=True): # 计算样本总数 num_examples = data.shape[0] data_processed = np.copy(data) # 预处理 features_mean = 0 features_deviation = 0 data_normalized = data_processed if normalize_data: ( data_normalized, features_mean, features_deviation ) = normalize(data_processed) data_processed = data_normalized # 特征变换sinusoid if sinusoid_degree > 0: sinusoids = generate_sinusoids(data_normalized, sinusoid_degree) data_processed = np.concatenate((data_processed, sinusoids), axis=1) # 特征变换polynomial if polynomial_degree > 0: polynomials = generate_polynomials(data_normalized, polynomial_degree) data_processed = np.concatenate((data_processed, polynomials), axis=1) # 加一列1 data_processed = np.hstack((np.ones((num_examples, 1)), data_processed)) return data_processed, features_mean, features_deviation
2、线性回归模块
写一个LinearRegression类,包含线性回归相关的方法。
import numpy as np from utils.features.prepare_for_training import prepare_for_training """线性回归""" class LinearRegression: def __init__(self, data, labels, polynomial_degree=0, sinusoid_degree=0, normalize_data=True): """ 1.对数据进行预处理操作 2.先得到所有的特征个数 3.初始化参数矩阵 """ (data_processed, features_mean, features_deviation) = prepare_for_training(data, polynomial_degree, sinusoid_degree) self.data = data_processed self.labels = labels self.features_mean = features_mean self.features_deviation = features_deviation self.polynomial_degree = polynomial_degree self.sinusoid_degree = sinusoid_degree self.normalize_data = normalize_data # 获取多少个列作为特征量 num_features = self.data.shape[1] # 1是列个数,0是样本个数 self.theta = np.zeros((num_features, 1)) # 构建θ矩阵 def train(self, alpha, num_iterations=500): """ 训练模块,执行梯度下降 :param alpha: α为学习率(步长) :param num_iterations: 迭代次数 :return: """ cost_history = self.gradient_descent(alpha, num_iterations) return self.theta, cost_history def gradient_descent(self, alpha, num_iterations): """ 梯度下降,实际迭代模块 :param alpha: 学习率 :param num_iterations: 迭代次数 :return: """ cost_history = [] # 保存损失值 for _ in range(num_iterations): # 每次迭代参数更新 self.gradient_step(alpha) cost_history.append(self.cost_function(self.data, self.labels)) return cost_history def gradient_step(self, alpha): """ 梯度下降参数更新计算方法(核心代码,矩阵运算) :param alpha: 学习率 :return: """ num_examples = self.data.shape[0] # 样本数 prediction = LinearRegression.hypothesis(self.data, self.theta) # 预测值 # 参差=预测值-真实值 delta = prediction - self.labels theta = self.theta # theta值更新,.T是执行转置 theta = theta - alpha * (1/num_examples)*(np.dot(delta.T, self.data)).T self.theta = theta def cost_function(self, data, labels): """ 损失计算 :param data: 数据集 :param labels: 真实值 :return: """ num_examples = data.shape[0] # 样本个数 # 参差=预测值-真实值 delta = LinearRegression.hypothesis(self.data, self.theta) - labels cost = (1/2)*np.dot(delta.T, delta) print(cost.shape) print(cost) return cost[0][0] @staticmethod def hypothesis(data, theta): """ 预测函数 :param data: :param theta: :return: """ # 如果处理的是一维数组,则得到的是两数组的內积;如果处理的是二维数组(矩阵),则得到的是矩阵积 predictions = np.dot(data, theta) return predictions def get_cost(self, data, labels): """ 计算当前损失 :param data: :param labels: :return: """ # 经过处理了的数据 data_processed = prepare_for_training(data, self.polynomial_degree, self.sinusoid_degree, self.normalize_data)[0] return self.cost_function(data_processed, labels) # 返回损失值 def predict(self, data): """ 用训练的数据模型,预测得到回归值结果 :param data: :return: """ # 经过处理了的数据 data_processed = prepare_for_training(data, self.polynomial_degree, self.sinusoid_degree, self.normalize_data)[0] predictions = LinearRegression.hypothesis(data_processed, self.theta) return predictions # 返回预测值
3、训练线性回归模型
对 LinearRegression类进行建模、预测、计算损失等。
import numpy as np import pandas as pd import matplotlib.pyplot as plt from linear_regression import LinearRegression """单变量线性回归""" data = pd.read_csv('../data/world-happiness-report-2017.csv') # 得到训练和测试数据集 train_data = data.sample(frac = 0.8) # sample:随机选取若干行 test_data = data.drop(train_data.index) # 将训练数据删除即为测试数据 # 数据和标签定义 input_param_name = "Economy..GDP.per.Capita." output_param_name = "Happiness.Score" x_train = train_data[[input_param_name]].values y_train = train_data[[output_param_name]].values x_test = test_data[[input_param_name]].values y_test = test_data[[output_param_name]].values plt.scatter(x_train, y_train, label="Train data") plt.scatter(x_test, y_test, label="Test data") plt.xlabel(input_param_name) plt.ylabel(output_param_name) plt.title('Happy') # 指定名字 plt.legend() plt.show() # 训练线性回归模型 num_iterations = 500 learning_rate = 0.01 # 学习率 linear_regression = LinearRegression(x_train, y_train) # 线性回归 (theta, cost_history) = linear_regression.train(learning_rate, num_iterations) # 执行训练 print('开始时的损失', cost_history[0]) print('训练后的损失', cost_history[-1]) # 最后一个 plt.plot(range(num_iterations), cost_history) plt.xlabel('Iteration') plt.ylabel('Cost') plt.title('GD') plt.show() # 测试 predications_num = 100 x_predications = np.linspace(x_train.min(), x_train.max(), predications_num).reshape(predications_num,1) y_predications = linear_regression.predict(x_predications) plt.scatter(x_train, y_train, label="Train data") plt.scatter(x_test, y_test, label="Test data") plt.plot(x_predications, y_predications, 'r', label="预测值") plt.xlabel(input_param_name) plt.ylabel(output_param_name) plt.title("Happy test") plt.legend() plt.show()
运行结果如下:
开始时的损失 1791.3527192463505
训练后的损失 26.382344732117332
输出图表:
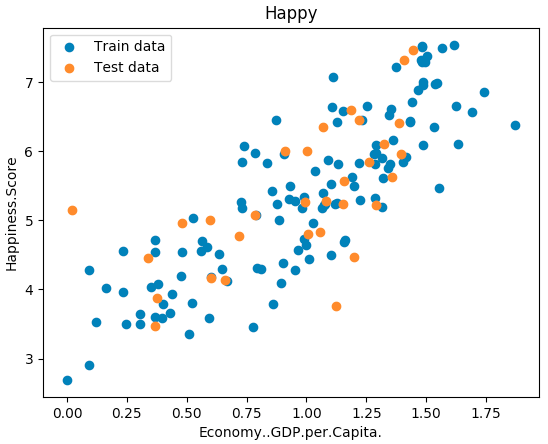
损失值:

线性回归方程:
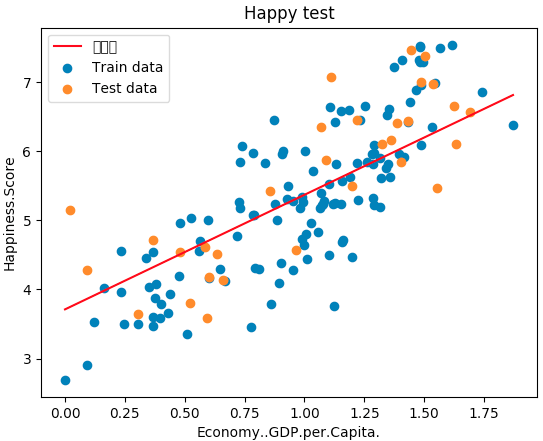
四、多特征回归模型
多特征建模,观察与单特征建模效果对比。
1、plotly工具包
Plotly 是一款用来做数据分析和可视化的在线平台,功能非常强大,可以在线绘制很多图形比如条形图、散点图、饼图、直方图等等。而且还是支持在线编辑,以及多种语言python、javascript、matlab、R等许多API。使用Plotly可以画出很多媲美Tableau的高质量图:
from plotly.graph_objs import Scatter,Layout import plotly import plotly.offline as py import numpy as np import plotly.graph_objs as go #setting offilne plotly.offline.init_notebook_mode(connected=True)
制作散点图:
trace1 = go.Scatter( y = np.random.randn(500), mode = 'markers', marker = dict( size = 16, color = np.random.randn(500), colorscale = 'Viridis', showscale = True ) ) data = [trace1] py.iplot(data)
把mode设置为markers就是散点图,然后marker里面设置一组参数,比如颜色的随机范围,散点的大小,还有图例等等。
推荐最好在jupyter notebook中使用,pycharm操作不是很方便。
2、代码实现
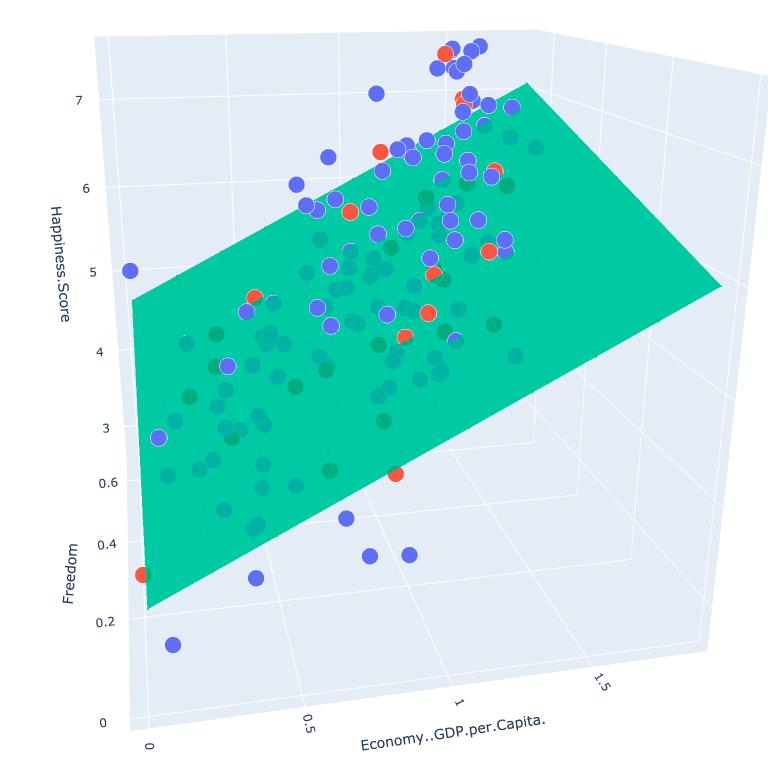
import numpy as np import pandas as pd import matplotlib.pyplot as plt import plotly # 交互式界面展示 import plotly.graph_objs as go plotly.offline.init_notebook_mode() from linear_regression import LinearRegression """单变量线性回归""" data = pd.read_csv('../data/world-happiness-report-2017.csv') # 得到训练和测试数据集 train_data = data.sample(frac = 0.8) # sample:随机选取若干行 test_data = data.drop(train_data.index) # 将训练数据删除即为测试数据 # 数据和标签定义 input_param_name_1 = "Economy..GDP.per.Capita." input_param_name_2 = "Freedom" output_param_name = "Happiness.Score" x_train = train_data[[input_param_name_1, input_param_name_2]].values y_train = train_data[[output_param_name]].values x_test = test_data[[input_param_name_1, input_param_name_2]].values y_test = test_data[[output_param_name]].values # 训练集 plot_training_trace = go.Scatter3d( x=x_train[:, 0].flatten(), y=x_train[:, 1].flatten(), z=y_train.flatten(), name="Training Set", mode="markers", marker={ 'size': 10, 'opacity': 1, 'line': { 'color': 'rgb(255, 255, 255)', 'width': 1 } } ) # 测试集 plot_test_trace = go.Scatter3d( x=x_test[:, 0].flatten(), y=x_test[:, 1].flatten(), z=y_test.flatten(), name="Test Set", mode="markers", marker={ 'size': 10, 'opacity': 1, 'line': { 'color': 'rgb(255, 255, 255)', 'width': 1 } } ) # 布局 plot_layout = go.Layout( title = 'Date Sets', scene = { 'xaxis': {'title': input_param_name_1}, 'yaxis': {'title': input_param_name_2}, 'zaxis': {'title': output_param_name} }, margin={'l': 0, 'r': 0, 'b': 0, 't': 0} ) plot_data = [plot_training_trace, plot_test_trace] plot_figure = go.Figure(data=plot_data, layout=plot_layout) plotly.offline.plot(plot_figure) # 弹出浏览器网页展示 num_iterations = 500 learning_rate = 0.01 # 学习率 polynomial_degree = 0 sinusoid_degree = 0 linear_regression = LinearRegression(x_train, y_train, polynomial_degree, sinusoid_degree) (theta, cost_history) = linear_regression.train( learning_rate, num_iterations ) print('开始损失', cost_history[0]) print('结束损失', cost_history[-1]) plt.plot(range(num_iterations), cost_history) plt.xlabel('Iterations') plt.ylabel('Cost') plt.title('Gradient Descent Progress') plt.show() predictions_num = 10 x_min = x_train[:, 0].min() x_max = x_train[:, 0].max() y_min = x_train[:, 1].min() y_max = x_train[:, 1].max() x_axis = np.linspace(x_min, x_max, predictions_num) y_axis = np.linspace(y_min, y_max, predictions_num) x_predictions = np.zeros((predictions_num * predictions_num, 1)) y_predictions = np.zeros((predictions_num * predictions_num, 1)) x_y_index = 0 for x_index, x_value in enumerate(x_axis): for y_index, y_value in enumerate(y_axis): x_predictions[x_y_index] = x_value y_predictions[x_y_index] = y_value x_y_index += 1 z_predictions = linear_regression.predict(np.hstack((x_predictions, y_predictions))) plot_predictions_trace = go.Scatter3d( x=x_predictions.flatten(), y=y_predictions.flatten(), z=z_predictions.flatten(), name='Prediction Plane', marker={ 'size': 1, }, opacity=0.8, surfaceaxis=2 ) plot_data = [plot_training_trace, plot_test_trace, plot_predictions_trace] plot_figure = go.Figure(data=plot_data, layout=plot_layout) plotly.offline.plot(plot_figure)
展示结果:
五、非线性回归模型
"""非线性回归""" import numpy as np import pandas as pd import matplotlib.pyplot as plt from linear_regression import LinearRegression data = pd.read_csv('../data/non-linear-regression-x-y.csv') x = data['x'].values.reshape((data.shape[0], 1)) y = data['y'].values.reshape((data.shape[0], 1)) data.head(10) # visualize the training and test datasets to see the shape of the data plt.plot(x, y) plt.show() # Set up linear regression parameters. num_iterations = 50000 learning_rate = 0.02 polynomial_degree = 15 # The degree of additional polynomial features. sinusoid_degree = 15 # The degree of sinusoid parameter multipliers of additional features. normalize_date = True # Init linear regression instance. # linear_regression = LinearRegression(x, y, normalize_date) # 线性回归 linear_regression = LinearRegression(x, y, polynomial_degree, sinusoid_degree, normalize_date) # Train linear regression (theta, cost_history) = linear_regression.train( learning_rate, num_iterations ) print('开始损失: {:.2f}'.format(cost_history[0])) print('结束损失: {:.2f}'.format(cost_history[-1])) theta_table = pd.DataFrame({'Model Parameters': theta.flatten()}) # Plot gradient descent progress. plt.plot(range(num_iterations), cost_history) plt.xlabel('Iterations') plt.ylabel('Cost') plt.title('Gradient Descent Progress') plt.show() # Get model predictions for the trainint set. predictions_num = 1000 x_predictions = np.linspace(x.min(), x.max(), predictions_num).reshape(predictions_num,1) y_predictions = linear_regression.predict(x_predictions) # Plot training data with predictions. plt.scatter(x, y, label='Training Dataset') plt.plot(x_predictions, y_predictions, 'r', label='Prediction') plt.show()
执行效果:
开始损失: 580629.11
结束损失: 8777.68
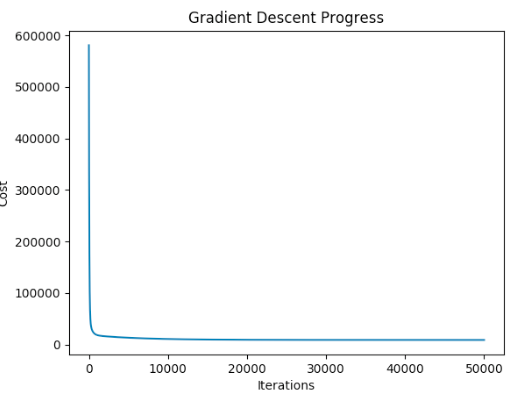
非线性回归方程:
