Ex 7_17 考虑如下的网络(其中数字为对应边的容量)...第十三次作业

(a) 利用ford-fulkerson算法即可求出最大流和最小分割。

(b) 剩余网络为

由S可达的顶点为A、B。可达T的顶点为C。

(c) 瓶颈边有e(A,C),e(B,C)。

(d) 下图中不包含瓶颈边。

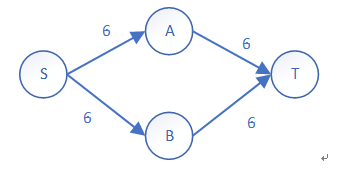
(e) 如果一条边e(u,v)是瓶颈边,首先这条边必须存在原图中,同时，在残量图中存在S到u的路径并且存在v到T的路径，所以在残量图中增加一条边e(u,v)后将使最大流的规模增加。首先在残量图中从S开始进行一次DFS求出从源点S可以到达的顶点集合W,然后在残量图的反向图中从T开始进行DFS求出可以到达T的顶点集合Y。最后遍历原图中的所有边e(u,v)，若uW并且vY，则e(u,v)是一条瓶颈边。

package org.xiu68.ch07.ex13;

import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.HashSet;
import java.util.Iterator;

public class Ex7_17 {

    public static void main(String[] args) {
        // TODO Auto-generated method stub
        int[][] c=new int[][]{
            {0,7,6,0,0,0},
            {0,0,0,4,2,0},
            {0,0,0,2,3,0},
            {0,0,0,0,0,9},
            {0,0,0,0,0,5},
            {0,0,0,0,0,0}
        };
        String[] vexs=new String[]{"S","A","B","C","D","T"};
        MGraph<String> m1=new MGraph<String>(c, vexs);
        m1.fordFulkerson(0, 5);
    }

}

class MGraph<T>{
    private int[][] c;        //容量矩阵
    private int[][] e;        //残量矩阵
    private int[][] f;        //当前流矩阵
    private int vexNum;        //顶点数量
    private String[] vexs;    //顶点表
    
    public MGraph(int[][] c,String[] vexs){
        this.c=c;
        this.vexNum=c.length;
        this.e=new int[vexNum][vexNum];
        this.f=new int[vexNum][vexNum];
        this.vexs=vexs;
        
        //刚开始时残量矩阵等于容量矩阵
        for(int i=0;i<vexNum;i++){
            System.arraycopy(c[i], 0, e[i], 0, c[i].length);
        }
        
    }
    
    //fordFulkerson算法
    public void fordFulkerson(int s,int t){
        int[] route=new int[vexNum];    //s到t的路径数组,route[i]表示i的前一个顶点
        
        while(bfs(s,t,route)){             //若还能找到一条路径
            
            //寻找路径中流最小的边的大小(在残量矩阵中)
            int min=Integer.MAX_VALUE;
            int tail=t;
            int head=route[t];

            while(head!=-1){
                if(e[head][tail]<min){
                    min=e[head][tail];
                }
                tail=head;
                head=route[head];
            }        
            
            //更新当前流矩阵和残量矩阵
            int tail1=t;
            int head1=route[tail1];
            while(head1!=-1){
                //更新当前流矩阵
                if(c[head1][tail1]!=0){        
                    f[head1][tail1]+=min;        //容量矩阵中存在边,增加head1到tail1的流的大小为min
                }else{
                    f[head1][tail1]-=min;        //容量矩阵中不存在边，撤销head1到tail1的流的大小为min
                }
                //更新残量矩阵
                e[head1][tail1]-=min;            //head1到tail1的流量减少min
                e[tail1][head1]+=min;            //tail1到head1的流量增加min
                
                tail1=head1;
                head1=route[head1];
            }//while
            //route=new int[vexNum];
            Arrays.fill(route, 0);                 //初始化路径数组
        }//while 还能找到一条s到t的路径
        
        //输出最大流
        int maxFlow=0;
        for(int i=0;i<vexNum;i++)                //最大流为  当前流矩阵中  从s流出的量
            maxFlow+=f[s][i];
        System.out.println("最大流为:"+maxFlow);
        
        //输出最小割
        System.out.print("最小割为(集合S)：");
        HashSet<Integer> cut=cut(s);
        for(Iterator<Integer> iter=cut.iterator();iter.hasNext();){
            System.out.print(vexs[iter.next()]+" ");
        }
        System.out.println();
        
        //输出瓶颈边
        System.out.println("瓶颈边有");
        HashSet<Edge> bottleneckEdgeSet=bottleneckEdge(s,t);
        for(Iterator<Edge> be=bottleneckEdgeSet.iterator();be.hasNext();){
            Edge ed=be.next();
            System.out.print("e("+vexs[ed.getHead()]+","+vexs[ed.getTail()]+") ");
        }
    }
    
    //广度优先搜索在残量图e中寻找s到t的路径
    public boolean bfs(int s,int t,int[] route){
        boolean[] visited=new boolean[vexNum];        //访问数组
        visited[s]=true;
        
        ArrayDeque<Integer> queue=new ArrayDeque<>();
        route[s]=-1;                                //设s的前一个顶点为-1
        
        for(int i=0;i<vexNum;i++){
            if(e[s][i]!=0 && !visited[i]){            //在残量矩阵中s到i存在一条路径
                queue.add(i);
                route[i]=s;
                visited[i]=true;
            }
        }
        
        while(!queue.isEmpty()){
            int middleVex=queue.poll();
            if(middleVex==t){
                return true;
            }else{
                for(int i=0;i<vexNum;i++){
                    if(e[middleVex][i]!=0 && !visited[i]){
                        queue.add(i);
                        route[i]=middleVex;
                        visited[i]=true;
                    }
                }
            }
        }//while
        return false;
    }
    
    //求最小割
    //在残量矩阵中,从s开始做一次搜索,从s能达到的所有的顶点都属于集合S
    public HashSet<Integer> cut(int s){
        boolean[] visited=new boolean[vexNum];
        HashSet<Integer> cut=new HashSet<>();    //保存最小割,集合S
        dfs(e,visited,cut,s);
        return cut;
    }
    //求瓶颈边
    public HashSet<Edge> bottleneckEdge(int s,int t){
        
        HashSet<Integer> w=new HashSet<>();        //从顶点S可以到达的顶点集合
        boolean[] visitedS=new boolean[vexNum];
        dfs(e,visitedS,w,s);                    //从顶点s开始进行深度优先搜索,求从顶点S可以到达的顶点集合
        
        
        //求残量图的反向图
        int[][] reverseE=new int[vexNum][vexNum];
        for(int i=0;i<vexNum;i++){
            for(int j=i+1;j<vexNum;j++){
                reverseE[i][j]=e[j][i];
                reverseE[j][i]=e[i][j];
            }
        }
        HashSet<Integer> y=new HashSet<>();        //从顶点S可以到达的顶点集合
        boolean[] visitedT=new boolean[vexNum];    
        dfs(reverseE,visitedT,y,t);                //从顶点t开始进行深度优先搜索,求从顶点T可以到达的顶点集合
        
        
        HashSet<Edge> bottleneckEdgeSet=new HashSet<>();
        //遍历原图中的所有边e(u,v),求u属于集合w，v属于集合y的边
        for(int i=0;i<vexNum;i++){
            for(int j=0;j<vexNum;j++){
                if(c[i][j]!=0 && w.contains(i) && y.contains(j)){
                    bottleneckEdgeSet.add(new Edge(i,j));
                }
            }
        }
        return bottleneckEdgeSet;
    }
    //深度优先搜索,记录搜索到的所有顶点
    private void dfs(int[][] edges,boolean[] visited,HashSet<Integer> set,int v){
        set.add(v);
        visited[v]=true;    
        for(int i=0;i<vexNum;i++){
            if(edges[v][i]!=0 && !visited[i]){
                dfs(edges,visited,set,i);
            }
        }
    }
}

class Edge{
    private int head;        //边的头
    private int tail;        //边的尾
    public Edge(int head, int tail) {
        super();
        this.head = head;
        this.tail = tail;
    }
    public int getHead() {
        return head;
    }
    public void setHead(int head) {
        this.head = head;
    }
    public int getTail() {
        return tail;
    }
    public void setTail(int tail) {
        this.tail = tail;
    }
    
}