【问题描述】
建立一个从源点S到终点E的有向无环图,设计一个动态规划算法求出从S到E的最短路径值,并输出相应的最短路径。
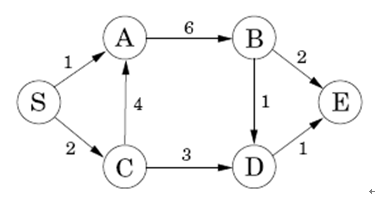
解:


1 package org.xiu68.exp.exp4; 2 3 import java.util.ArrayDeque; 4 import java.util.Stack; 5 6 public class Exp4_2 { 7 //建立一个从源点S到终点E的有向无环图,设计一个动态规划算法求出从S到E的最短路径值,并输出相应的最短路径。 8 public static void main(String[] args) { 9 int m=Integer.MAX_VALUE; 10 int[][] edges=new int[][]{ 11 {m,1,m,2,m,m}, 12 {m,m,6,m,m,m}, 13 {m,m,m,m,1,2}, 14 {m,4,m,m,3,m}, 15 {m,m,m,m,m,1}, 16 {m,m,m,m,m,m} 17 }; 18 MGraph1 m1=new MGraph1(edges); 19 m1.minPath(0, 5); 20 //输出 21 // 0 to 5 is 6 22 // the path is:0-->3-->4-->5 23 24 } 25 } 26 27 class MGraph1{ 28 private int[][] edges; //有向无环图 29 private int vexNum; //顶点数量 30 31 public MGraph1(int[][] edges){ 32 this.edges=edges; 33 this.vexNum=edges.length; 34 } 35 36 public void minPath(int start,int end){ 37 38 int[] dist=new int[vexNum]; //源点到该点的最短路径 39 for(int i=0;i<vexNum;i++) 40 dist[i]=Integer.MAX_VALUE; 41 dist[start]=0; 42 43 int[] pre=new int[vexNum]; //最短路径中该点的前一个顶点 44 pre[start]=-1; 45 46 Stack<Integer> queue=new Stack<>(); //存放拓扑排序序列 47 topoSort(queue); 48 49 while(!queue.isEmpty()){ 50 int j=queue.pop(); 51 52 for(int i=0;i<vexNum;i++){ 53 if(edges[i][j]!=Integer.MAX_VALUE && dist[j]>dist[i]+edges[i][j]){ 54 dist[j]=dist[i]+edges[i][j]; 55 pre[j]=i; 56 } 57 }//for 58 }//while 59 60 //打印最短路径 61 System.out.println(start+" to "+end+" is "+dist[end]); 62 63 String path=""+end; 64 int preVex=pre[end]; 65 66 while(preVex!=-1){ 67 path=preVex+"-->"+path; 68 preVex=pre[preVex]; 69 } 70 System.out.println("the path is:"+path); 71 72 } 73 74 //拓扑排序 75 public void topoSort(Stack<Integer> queue){ 76 boolean[] visited=new boolean[vexNum]; 77 for(int i=0;i<vexNum;i++){ 78 if(!visited[i]) 79 dfs(queue,i,visited); 80 } 81 } 82 83 //利用深度优先搜索进行拓扑排序 84 public void dfs(Stack<Integer> queue,int v,boolean[] visited){ 85 visited[v]=true; 86 for(int i=0;i<vexNum;i++){ 87 if(edges[v][i]!=Integer.MAX_VALUE && !visited[i]) 88 dfs(queue,i,visited); 89 } 90 queue.push(v); 91 } 92 }
