前言
上一篇博客为大家介绍了数组与链表这两种数据结构,虽然它们在某些方面有着自己的一些优点,但是也存在着一些自身的缺陷,本篇博客为将为大家介绍一下数据结构---二叉树,它在保留数组和链表的优点的同时也改善了它们的缺点(当然它也有着自己的缺点,同时它的实现也比较复杂).
1. 数组和链表的特点
数组的优点:
- 简单易用.
- 无序数组的插入速度很快,效率为O(1)
- 有序数组的查找速度较快(较无序数组),效率为O(logN)
数组的缺点:
- 数组的查找、删除很慢
- 数组一旦确定长度,无法改变
链表的优点:
- 可以无限扩容(只要内存够大)
- 在链表头的新增、删除很快,效率为O(1)
链表的缺点:
- 查找很慢
- 在非链表头的位置新增、删除很慢,效率为O(N)
2.树和二叉树
树是一种数据结构,因为它数据的保存形式很像一个树,所以得名为树(树状图).
而二叉树是一种特殊的树,它的每个节点最多含有两个子树,现实世界中的二叉树:

图1
但是实际中的二叉树却是倒挂的,如图:

图2
二叉树的名词解释:
- 根:树顶端的节点称为根。一棵树只有一个根,如果要把一个节点和边的集合称为树,那么从根到其他任何一个节点都必须有且只有一条路径。A是根节点。
- 父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;B是D的父节点。
- 子节点:一个节点含有的子树的根节点称为该节点的子节点;D是B的子节点。
- 兄弟节点:具有相同父节点的节点互称为兄弟节点;比如上图的D和E就互称为兄弟节点。
- 叶节点:没有子节点的节点称为叶节点,也叫叶子节点,比如上图的E、H、L、J、G都是叶子节点。
- 子树:每个节点都可以作为子树的根,它和它所有的子节点、子节点的子节点等都包含在子树中。
- 节点的层次:从根开始定义,根为第一层,根的子节点为第二层,以此类推。
- 深度:对于任意节点n,n的深度为从根到n的唯一路径长,根的深度为0;
- 高度:对于任意节点n,n的高度为从n到一片树叶的最长路径长,所有树叶的高度为0;
深度与高度的区别在于: 深度为根到节点的距离,而高度是节点到叶的距离(记住根深叶高)。
3.二叉搜索树以及它是通过什么方式改善的数组、链表的问题
二叉搜索树是一种特殊的二叉树,除了它的子节点不能超过两个以外,它还拥有如下特点:
- 一个节点的左子节点的关键字的值永远小于该节点的值
- 一个节点的右子节点的关键字的值永远大于等于该节点的值
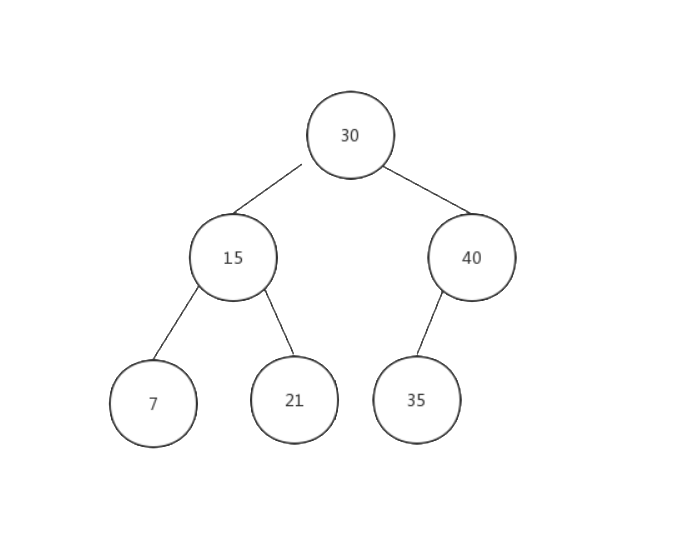
图3 - 二叉搜索树关键字的排序方式
从图3还可以看出,二叉搜索树的最小值就是它的最左节点的关键字的值,而最大值则是它的最右节点的值.
二叉搜索树的查找、新增、删除的效率为O(logN)(这是理想状态下,如果树是不平衡的效率会降到O(N),后面会介绍).
二叉搜索树之所以效率高就在于:
- 它的数据是按照上述的有序的方式排列的.
- 进行新增、查找、删除的时候使用了二分查找法.
4. 二叉树的实现
二叉树中数据是保存在一个个的节点中的,下面是保存数据的节点类:
/**
* @author liuboren
* @Title: 节点类
* @Description:
* @date 2019/11/28 9:33
*/
public class Node {
// 用来进行排序的关键字数组
int sortData ;
// 其他类型的数据
int other;
// 该节点的左子节点
Node leftNode;
// 该节点的右子节点
Node rightNode;
public static void main(String[] args) {
Node node = new Node();
System.out.println("node.leftNode = " + node.leftNode);
System.out.println(node.leftNode);
}
}
在二叉搜索树这个类中新增、修改、删除数据:
public class Tree {
// 根节点
Node root;
public Tree(Node root) {
this.root = root;
}
// 新增、查找、删除 暂时省略,下面会一一介绍
}
4.1 新增数据
在二叉树中插入数据的流程如下:
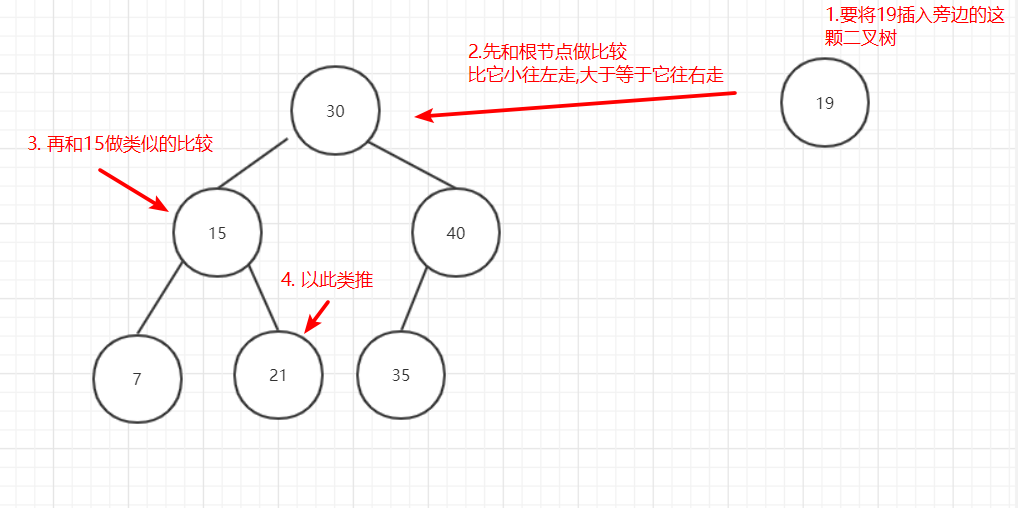
图4
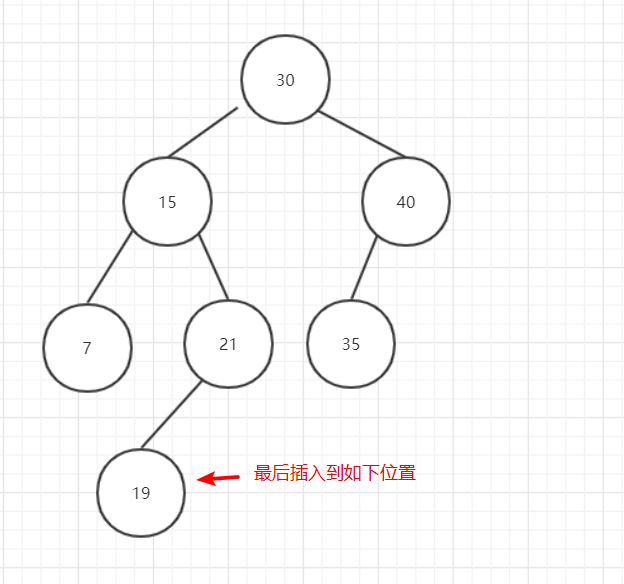
图5
Java代码:
/*新增数据*/
public void insertData(Node node) {
int currentSortData = root.sortData;
Node currentNode = root;
Node currentLeftNode = root.leftNode;
Node currentRightNode = root.rightNode;
int insertSortData = node.sortData;
while (true) {
if (insertSortData < currentSortData) {
if (currentLeftNode == null) {
currentNode.leftNode = node;
break;
} else {
currentNode = currentNode.leftNode;
currentLeftNode = currentNode.leftNode;
currentRightNode = currentNode.rightNode;
currentSortData = currentNode.sortData;
}
} else {
if (currentRightNode == null) {
currentNode.rightNode = node;
break;
} else {
currentNode = currentNode.rightNode;
currentSortData = currentNode.sortData;
currentLeftNode = currentNode.leftNode;
currentRightNode = currentNode.rightNode;
}
}
}
System.out.println("root = " + root);
}
4.3 查找方法
流程与插入方法类似.
Java代码:
public void query(int sortData) {
Node currentNode = root;
while (true) {
if (sortData != currentNode.sortData) {
if (sortData < currentNode.sortData) {
if (currentNode.leftNode != null) {
currentNode = currentNode.leftNode;
} else {
System.out.println("对不起没有查询到数据");
}
} else {
if (currentNode.rightNode != null) {
currentNode = currentNode.rightNode;
} else {
System.out.println("对不起没有查询到数据");
}
}
} else {
System.out.println("二叉树中有该数据");
}
}
}
4.3 删除方法
删除节点要分三种情况.
- 删除节点无子节点的情况
- 删除节点有一个子节点的情况
- 删除节点有两个子节点的情况
删除节点无子节点的情况是最简单的,直接将该节点置为null就可以了:
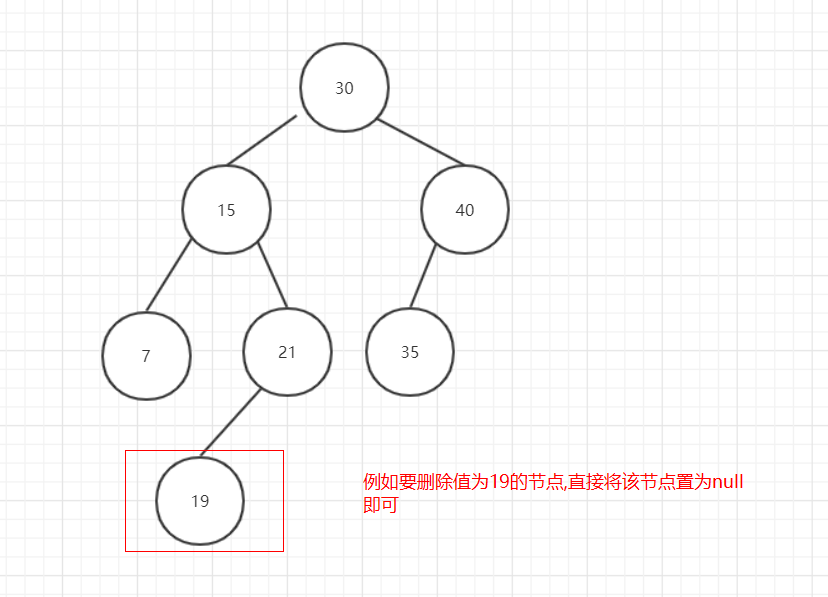
图6
删除节点有一个子节点的情况:

图7
删除后:
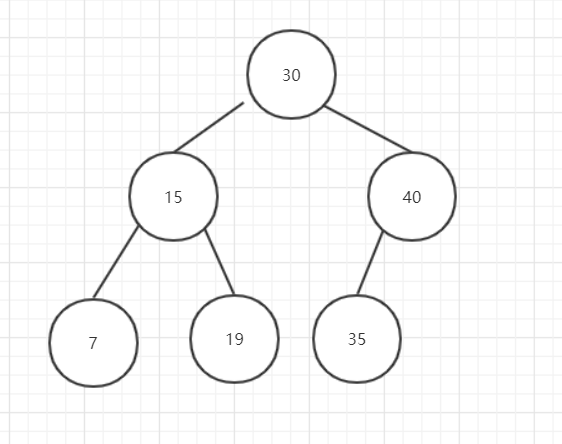
图8
最复杂的删除节点有两个子节点的情况,删除流程如下:
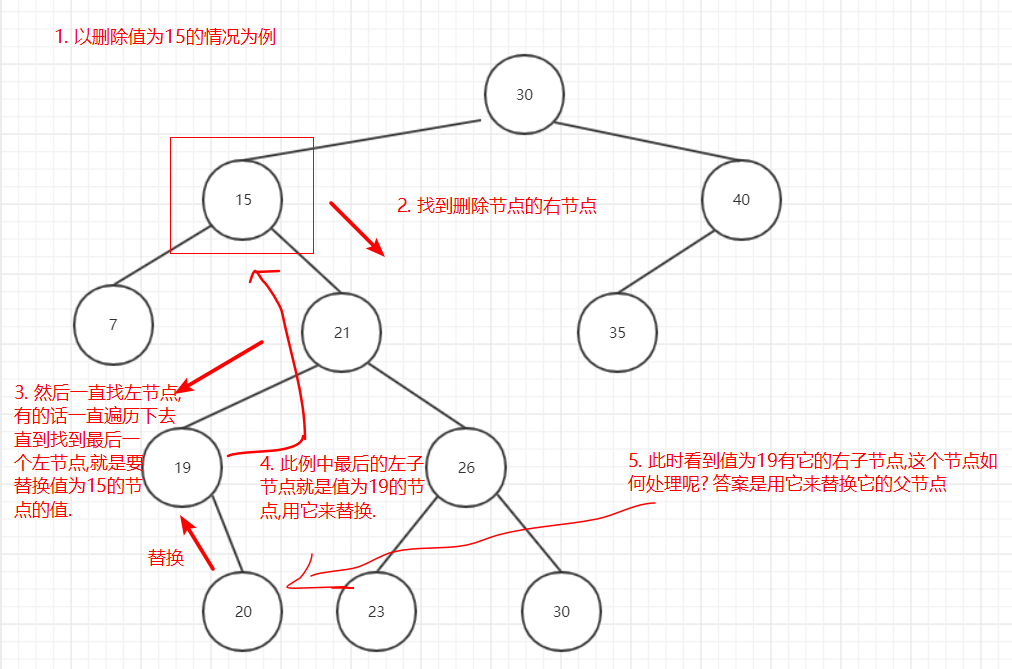
图9
删除后:
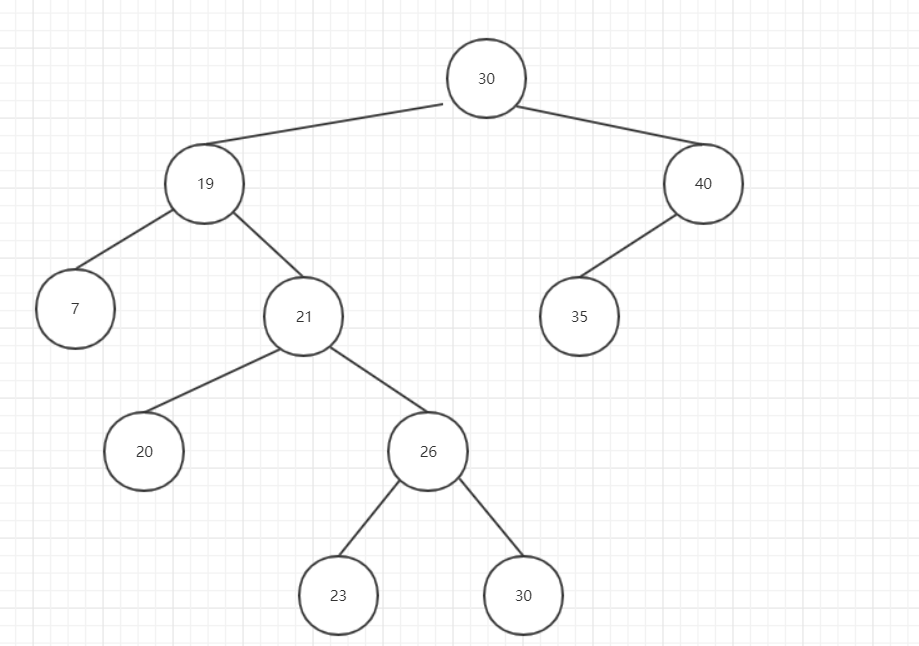
图10
为什么要以这种方式删除节点呢? 再次回顾一下二叉搜索树的特点:
- 一个节点的左子节点的关键字的值永远小于该节点的值
- 一个节点的右子节点的关键字的值永远大于等于该节点的值
之所以要找删除节点的右子节点的最后一个左节点,是因为这个值是删除节点的子节点中最小的值,为了满足上面的这两个特点,所以删除要以这种算法去实现.
Java代码:
public boolean delete(int deleteData) {
Node curr = root;
Node parent = root;
boolean isLeft = true;
while (deleteData != curr.sortData) {
if (deleteData <= curr.sortData) {
isLeft = true;
if (curr.leftNode != null) {
parent = curr;
curr = curr.leftNode;
}
} else {
isLeft = false;
if (curr.rightNode != null) {
parent = curr;
curr = curr.rightNode;
}
}
if (curr == null) {
return false;
}
}
// 删除节点没有子节点的情况
if (curr.leftNode == null && curr.rightNode == null) {
if (curr == root) {
root = null;
} else if (isLeft) {
parent.leftNode = null;
} else {
parent.rightNode = null;
}
//删除节点只有左节点
} else if (curr.rightNode == null) {
if (curr == root) {
root = root.leftNode;
} else if (isLeft) {
parent.leftNode = curr.leftNode;
} else {
parent.rightNode = curr.leftNode;
}
//如果被删除节点只有右节点
} else if (curr.leftNode == null) {
if (curr == root) {
root = root.rightNode;
} else if (isLeft) {
parent.leftNode = curr.rightNode;
} else {
parent.rightNode = curr.rightNode;
}
} else {
Node successor = getSuccessor(curr);
if (curr == root) {
root = successor;
} else if (curr == parent.leftNode) {
parent.leftNode = successor;
} else {
parent.rightNode = successor;
}
successor.leftNode = curr.leftNode;
}
return true;
}
public Node getSuccessor(Node delNode) {
Node curr = delNode.rightNode;
Node successor = curr;
Node sucParent = null;
while (curr != null) {
sucParent = successor;
successor = curr;
curr = curr.leftNode;
}
if (successor != delNode.rightNode) {
sucParent.leftNode = successor.rightNode;
successor.rightNode = delNode.rightNode;
}
return successor;
}
5. 遍历
遍历二叉树中的数据,有三种遍历方式:
- 前序
- 中序(最常用)
- 后续
前序、中序和后序三种遍历方式的步骤是相同的,只是顺序不同.
前序遍历顺序:
- 先输出当前节点
- 再遍历左子节点
- 再遍历右子节点
中序遍历顺序:
- 先遍历左子节点
- 再输出当前节点
- 再遍历右子节点
后序遍历顺序:
- 先遍历左子节点
- 再遍历又子节点
- 再输出当前节点
什么当前节点?什么左右子节点?太抽象!!!!没关系继续看图.
前序遍历输出顺序图:
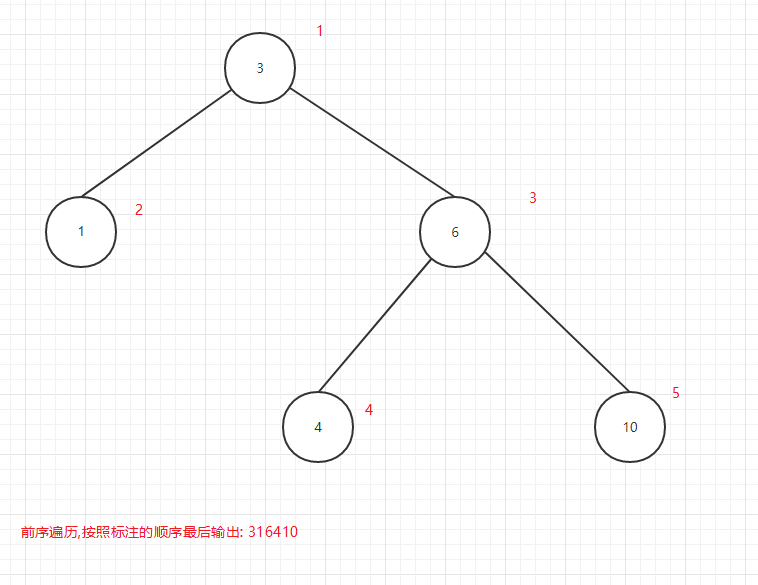
图11
中序遍历输出顺序图:
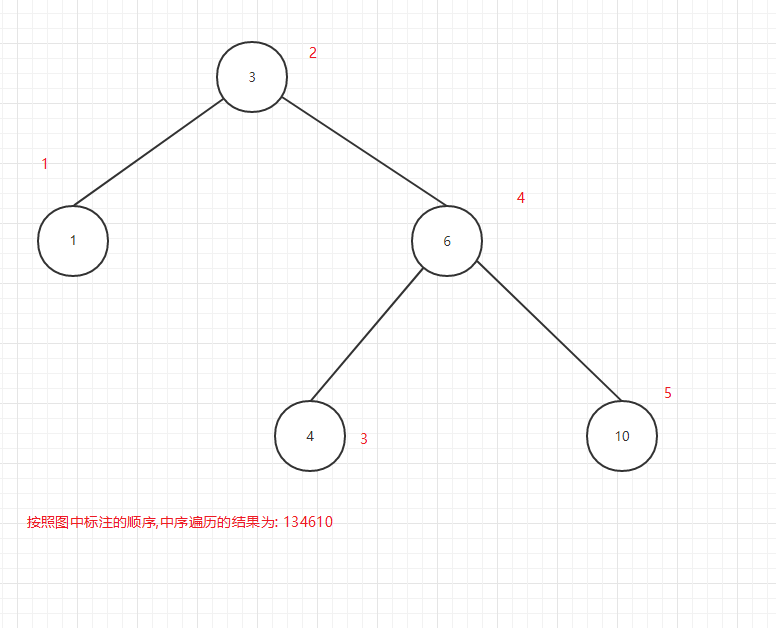
图12
后序遍历输出顺序图:
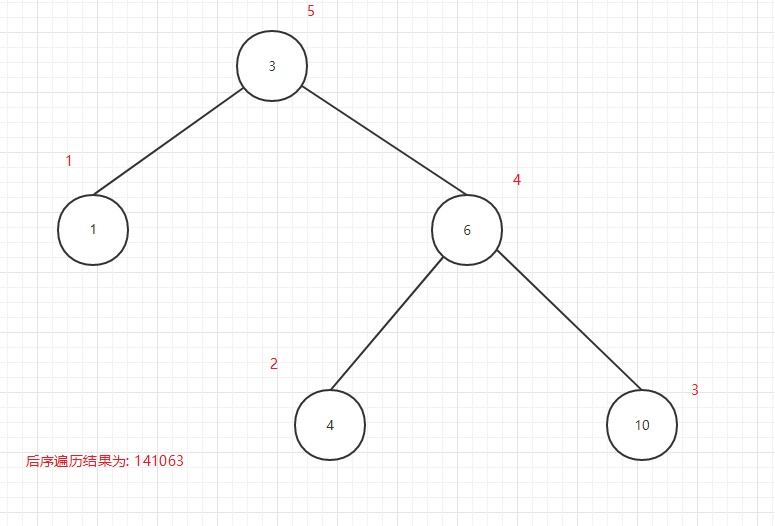
图13
可以看出所谓的前中后序是输出当前节点的顺序,前序是在第一个输出当前节点,中序是第二个输出当前节点,后序是第三个当前节点.
又因为中序遍历是按照关键值由小到大的顺序输出的,所以中序遍历最为常用.
前、后序遍历在解析或分析二叉树(不是二叉搜索树)的算术表达式的时候比较有用,用的不太多,看下图:
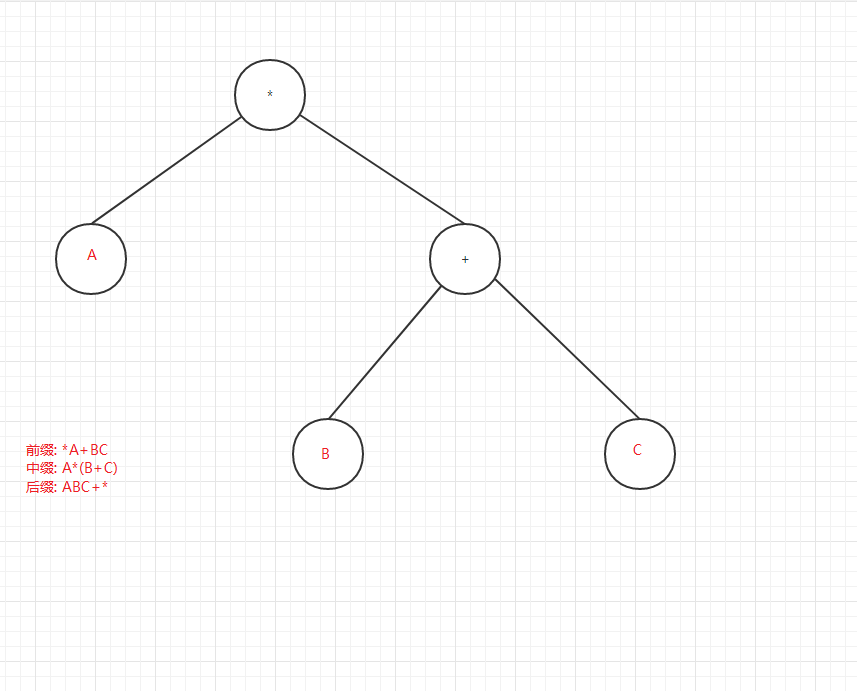
6. 二叉树的效率
我们用二叉树与数组和链表进行对比,在有100w个数据项的无序数组或链表中,查找数据项平均会比较50w次,但在有100w个节点的树中,只需要20(或更少)次的比较.
有序数组可以很快的找到数据项,但插入数据项平均需要移动50w个数据项,在100w个节点的树中插入数据项需要比较20或更少次的比较,再加上很短的时间来连接数据项.
同样,从有100w个数据项的数组中删除一个数据项需要平均移动50w个数据项,而在100w个节点的树中删除节点只需要20次或更少的比较来找到它,再加上(可能的话)一点比较的时间来找到它的后继,一点时间来断开这个节点的链接,以及连接它的后继.
结论: 树对所有常用的数据存储操作都有很高的效率
遍历不如其他操作快. 但是,遍历在大型数据库中不是常用的操作.它更长用于程序中的辅助方法来解析算术或其他的表达式,而且表达式一般都不会很长.
如果二叉树是平衡的,它的效率为: O(logN),如果二叉树是不平衡的(最极端的情况,存入树中的数据是升序或降序排列的,那么二叉树就是链表),效率为: O(N)
所以二叉搜索树在保存随机数值的时候,效率才是最高的
7. 二叉树的缺点
如果二叉树是极端不平衡的(此时的二叉树就是一个链表),它的效率为O(N),即使数值是随机的,如果数据的量够大,也有可能有一部分的数值是有序的(就像你抛硬币的时间足够长,会有一段时间出现一直抛正面或反面),造成二叉树会变成是局部不平衡的,这样它的效率会介于O(logN)到O(N).
如何使二叉树的效率始终保持在O(logN)呢? 下篇博客为您介绍红黑树.