题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=3551
题意:有一个n个点,m条边的图 ,给出每个点的度数,问是否可以成为该图的子图。
不看大佬的博客是真的想不出来。。。
思路:主要是建图,建完只要跑下一般图最大匹配就可以。但是这个图真难啊!!!
将每个度数拆成一个个点,重新编号,拆完的点连向对应的x,y点。
例如例题1:
4 4
1 2
3 4
2 3
1 4
1
2
1
0
按照 度数将 1的1个度编号为1, 2的2个度编号为2和3, 3的一个度编号为4
在根据原图连接拆点(当然边也要拆点)。
由 第一条边1---2: 将1点变成 5, 2变成 6 将每个度的拆点与其对应边的拆点连接
就是现在1的度拆点1和边拆5相连 2的度拆点 2和3 与边拆点 6相连
连接方式: 1--5 2--6 3--6 当然 5---6
第二条边 3---4 将3点变成 7, 4变成8
连边方式:4---7 7---8
第三条边 2---3 将2点变成 9, 3变成10
连边方式:2---9 3---9 4---10 9---10
第四条边 1---4 将1点变成11, 4变成12
连边方式:1---11 11---1
图如下:
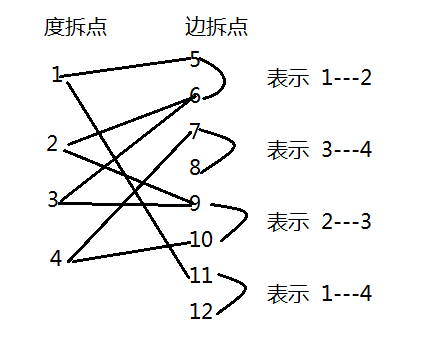
最大匹配: 1---5 2---6 3---9 4---10 7---8 11---12 达到完美匹配所以是可以成为子图的
再求最大匹配,如果是完美匹配就是子图。
为什么?
如果达到完美匹配,这条边的另一头必定匹配着另一个点的一个度,表示拆点原点相连,这样一条边的匹配是合乎要求的。
例如上面 1--5 2--6 就是1的一个度连接2的一个度 3--9 4--10就是2的一个度连接3的一个度
而7---8 11---12表示 应该删除原先边3---4 1---4. 就是子图的样子即子图 1---2 2---3
即最大匹配中度的拆点与边的拆点匹配时就是子图中连接边的一个点 而通过边拆点的连接连向另一个点, 而只有边的拆点与边的拆点相连 就是删除的边
代码:
#include<iostream> #include<algorithm> #include<cstdio> #include<cstring> #include<queue> #define inf 0x3f3f3f3f using namespace std; typedef long long ll; const int maxn=1050; bool g[maxn][maxn],inque[maxn],inpath[maxn]; bool inhua[maxn]; int st,ed,newbase,ans,n; int base[maxn],pre[maxn],match[maxn]; int head,tail,que[maxn]; int x[maxn],y[maxn],f[maxn],mp[maxn][maxn],ne,np; void Push(int u) { que[tail]=u; tail++; inque[u]=1; } int Pop() { int res=que[head]; head++; return res; } int lca(int u,int v)//寻找公共花祖先 { memset(inpath,0,sizeof(inpath)); while(1) { u=base[u]; inpath[u]=1; if(u==st) break; u=pre[match[u]]; } while(1) { v=base[v]; if(inpath[v]) break; v=pre[match[v]]; } return v; } void reset(int u)//缩环 { int v; while(base[u]!=newbase) { v=match[u]; inhua[base[u]]=inhua[base[v]]=1; u=pre[v]; if(base[u]!=newbase) pre[u]=v; } } void contract(int u,int v)// { newbase=lca(u,v); memset(inhua,0,sizeof(inhua)); reset(u); reset(v); if(base[u]!=newbase) pre[u]=v; if(base[v]!=newbase) pre[v]=u; for(int i=1;i<=n;i++) { if(inhua[base[i]]){ base[i]=newbase; if(!inque[i]) Push(i); } } } void findaug() { memset(inque,0,sizeof(inque)); memset(pre,0,sizeof(pre)); for(int i=1;i<=n;i++)//并查集 base[i]=i; head=tail=1; Push(st); ed=0; while(head<tail) { int u=Pop(); for(int v=1;v<=n;v++) { if(g[u][v]&&(base[u]!=base[v])&&match[u]!=v) { if(v==st||(match[v]>0)&&pre[match[v]]>0)//成环 contract(u,v); else if(pre[v]==0) { pre[v]=u; if(match[v]>0) Push(match[v]); else//找到增广路 { ed=v; return ; } } } } } } void aug() { int u,v,w; u=ed; while(u>0) { v=pre[u]; w=match[v]; match[v]=u; match[u]=v; u=w; } } void edmonds()//匹配 { memset(match,0,sizeof(match)); for(int u=1;u<=n;u++) { if(match[u]==0) { st=u; findaug();//以st开始寻找增广路 if(ed>0) aug();//找到增广路 重新染色,反向 } } } //以上是带花树求最大匹配算法 不用看 void create()//建图 { n=0; memset(g,0,sizeof(g)); for(int i=1;i<=np;i++) for(int j=1;j<=f[i];j++) mp[i][j]=++n;//拆点,给每个度的点编号 for(int i=0;i<ne;i++) {//此时n+1代表x,n+2代表y for(int j=1;j<=f[x[i]];j++) g[mp[x[i]][j]][n+1]=g[n+1][mp[x[i]][j]]=1;//每个度的点与对应的x,y相连 for(int j=1;j<=f[y[i]];j++) g[mp[y[i]][j]][n+2]=g[n+2][mp[y[i]][j]]=1; g[n+1][n+2]=g[n+2][n+1]=1;//x与y相连 n+=2; } } void print() { ans=0; for(int i=1;i<=n;i++) if(match[i]!=0) { ans++; // if(match[i]>i) // cout<<"_____"<<i<<' '<<match[i]<<endl; } //cout<<"******"<<ans<<' '<<n<<endl; if(ans==n) printf("YES "); else printf("NO "); } int main() { int t,k=0; scanf("%d",&t); while(t--) { scanf("%d%d",&np,&ne); for(int i=0;i<ne;i++) scanf("%d%d",&x[i],&y[i]); for(int i=1;i<=np;i++) scanf("%d",&f[i]); printf("Case %d: ",++k); create(); edmonds(); print(); } return 0; }