| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 3018 | Accepted: 1010 |
Description
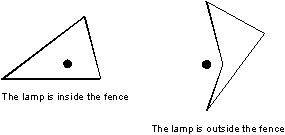
Input
Output
Sample Input
0.5 1.7 3 1.0 3.0 2.0 -1.0 -4.0 -1.0
Sample Output
5.34
题目大意:求一个用篱笆围成的多边形对灯泡发出的光单位时间吸收的能量,灯泡发出的光射到篱笆上不穿透,不反射,不衍射(即篱笆受到的光能全部吸收)。
光照强度公式:I0=k/r(I0光照强度,k固定系数,r光照点到光源的距离)
对于某一小段线段的光能量公式:dI=I0*|cosα|*dl*h(di单位时间吸收的光能,I0此处的光照强度,dl一小段篱笆的长度,h篱笆的高度,α光在这小段篱笆上的入射角的余角(设b为入射角,那么α=90-b))
设光源到这条边的距离为t:
dI=I0*|cosα|*dl*h (cosα=t/r)
=k/r*t/r*h*dl
=h*k*t/(r*r)*dl
=hkt/(t*t+l*l)*dl
l是自变量,hkt是定量,对1/(t*t+l*l)*dl积分。
根据定积分可求出这一条篱笆单位时间吸收的能量:
∫1/(t^2+l^2)dl
根据定积分公式:∫1/(a^2+x^2)dx=1/a*arctan(x/a)+c
得:∫1/(t^2+l^2)dl=1/t*arctan(l/t)+c
所以 ∫kht/(t^2+l^2)dl=kh*arctan(l/t)+c
tan(a)=l/t
接下来求原点光源发散出的光被边覆盖的总弧度和。 每条边都有它的起始极角跟终点极角,它们的角度差就为这条变覆盖光的弧度大小, 由于光不能穿透,所以有重叠的地方只能计算一遍,以x轴正方向为起始位置,光源周围的范围为(0-2*PI),每条边都有他的范围,接下来求区间覆盖就行了。 需要注意的地方:有些边穿过x正半轴这样不好处理,因此把这样的边以x正半轴切成两条边(使得每条边的起始极角都<=0,便于求区间覆盖问题)
真JB操蛋,多组案例输入就一直WA。
#include <iostream>
#include <cmath>
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
struct Point{
double x,y;
Point(){}
Point(double x,double y):x(x),y(y){}
};
struct Seg{
double s,e;
};
typedef Point Vector;
Vector operator +(Vector A,Vector B){return Vector(A.x+B.x,A.y+B.y);}
Vector operator -(Vector A,Vector B){return Vector(A.x-B.x,A.y-B.y);}
Vector operator *(Vector A,double p){return Vector(A.x*p,A.y*p);}
Vector operator /(Vector A,double p){return Vector(A.x/p,A.y/p);}
bool operator < (const Point &a,const Point &b)
{
return a.x<b.x||(a.x==b.x&&a.y<b.y);
}
const double eps=1e-10;
const double PI=acos(-1*1.0);
int dcmp(double x)
{
if(fabs(x)<eps) return 0;
else return x<0?-1:1;
}
bool operator == (const Point &a,const Point &b){
return (dcmp(a.x-b.x)==0 && dcmp(a.y-b.y)==0);
}
double Dot(Vector A,Vector B){return A.x*B.x+A.y*B.y;}//点积
double Length(Vector A){return sqrt(Dot(A,A));}//向量长度
double Angle(Vector A,Vector B){return acos(Dot(A,B)/Length(A)/Length(B));}//两向量的夹角
double Cross(Vector A,Vector B){ return A.x*B.y-A.y*B.x;}//叉积
double angle(Point p){ return atan2(p.y,p.x);}
double DistanceToLine(Point P,Point A,Point B)//点到直线的距离
{
Vector v1=B-A,v2=P-A;
return fabs(Cross(v1,v2)) / Length(v1);
}
Point read_point()
{
Point P;
scanf("%lf %lf",&P.x,&P.y);
return P;
}
vector<Point> p;
vector<Seg> s;
bool mycomp(const Seg &a,const Seg &b)
{
if(dcmp(a.s-b.s) != 0) return a.s<b.s;
else return a.e<b.e;
}
void swap(double &a,double &b)
{
double t=a;
a=b;b=t;
}
double GetAngle(Point a)
{
double ang=angle(a);
if(dcmp(ang) < 0) ang+=2*PI;
return ang;
}
void SegmentDeal()
{
int i,j,n=p.size();
Seg s1,s2;
for(i=0;i<n;i++)
{
j=(i+1)%n;
s1.s=GetAngle(p[i]);s1.e=GetAngle(p[j]);
if(dcmp(s1.s-s1.e) > 0) swap(s1.s,s1.e);
if(dcmp(s1.e-s1.s-PI) > 0)
{
s2.s=0;s2.e=s1.s;
s1.s=s1.e;s1.e=2*PI;
s.push_back(s2);
}
s.push_back(s1);
}
sort(s.begin(),s.end(),mycomp);
}
double solve()
{
int i,n;
double L,R;
double ans=0;
SegmentDeal();
n=s.size();L=s[0].s;R=s[0].e;
for(i=1;i<n;i++)
{
if(dcmp(s[i].s-R) <= 0)
{
if(dcmp(s[i].e-R) > 0) R=s[i].e;
}
else
{
ans=R-L;
L=s[i].s;
R=s[i].e;
}
}
ans+=R-L;
return ans;
}
int main()
{
int n,i;
double h,k,ans;
scanf("%lf %lf %d",&k,&h,&n);
p.clear();s.clear();
for(i=0;i<n;i++) p.push_back(read_point());
ans=solve();
printf("%.2lf
",ans*h*k);
return 0;
}