作者：桂。
时间：2017-09-09 12:48:45
链接：http://www.cnblogs.com/xingshansi/p/7498175.html
一、复数相乘
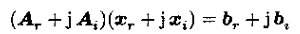
可以表示为分块的形式：
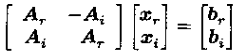
二、范数
A-范数基本定义
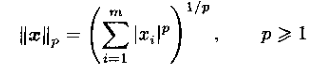
p = 0，0范数，对应非零元素个数；
p = 1，1范数，也成和范数；
p = 2，常称为Euclidean范数，也成Frobenius范数
p = ∞， 无穷范数，也称极大范数。
直接定义p，则p范数或Minkowski p范数，也叫Holder范数。
B-其他常用范数
1-谱范数（spectrum norm）
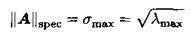
其中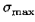
是矩阵A的最大奇异值，即
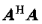最大特征值的正平方根。
谱范数也称最大奇异值范数或者算子范数（operator norm）。
2-Mahalanobis范数
其中
是正定矩阵。
三、矩阵的迹
A-迹的一般性质
迹等于特征值之和：
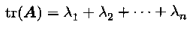
而根据SVD分解特性（PCA、KL变换均有用到），可知特征值体现的是能量，故矩阵的迹可以与Euclidean范数建立联系：
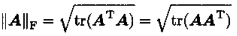
B-迹的其他特性
其实矩阵的迹，借助矩阵分解来理解会容易很多，迹的其他特性：
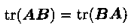
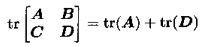
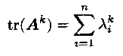
由于1标量可以，其本身看作与迹等价，从而有（tr(AB)=tr(BA)、对角和=迹，借助这两条性质可证）：
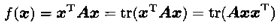
C-迹的微分特性
1）若W是mxm的矩阵：
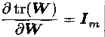
2）若W可逆：
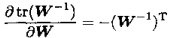
3）对于矩阵W、A，有
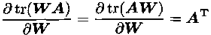
4）若W非奇异，
5）对于矩阵W、A：
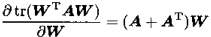
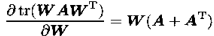
6）对于矩阵W、A、B，且W非奇异：
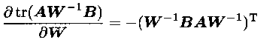
四、行列式
给出行列式定义：
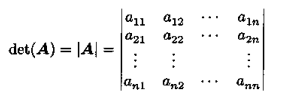
对于一个三角矩阵A：
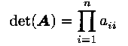
另外，
五、矩阵求逆
A-矩阵求逆基本性质
若ABC可逆：
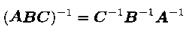
若A为对角阵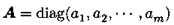
：
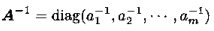
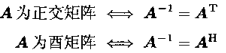
若A非奇异：
B-矩阵求逆引理
求逆引理，也称Sherman-Morrison公式：若A是一个nxn的可逆矩阵，且x和y是两个nx1的向量，使得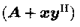 
可逆，则：
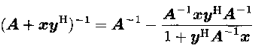
该引理可进一步推广为矩阵之和的求逆公式：
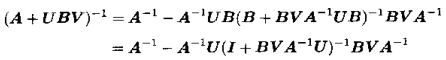
简化的形式：
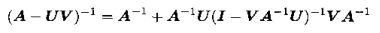
分块矩阵求逆：
1）若A可逆：
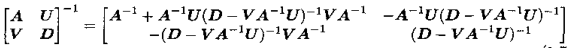
2）若A、D均可逆：
C-广义逆矩阵
广义逆矩阵参考之前的博文。
六、Hadamard积与Kronecker积
A-矩阵的直和
mxm的矩阵A与nxn的矩阵B，其直和记作：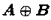
，它是一个(m+n)x(m+n)的矩阵，
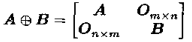
B-Hadamard积
Hadamard积其实就是对应元素相乘。
两个mxn的矩阵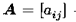
、
，其Hadamard积记作：
，
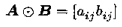
C-Kronecker积
Kronecker积表示的是矩阵元素与另一矩阵相乘的运算，用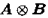
表示。
1）右Kronecker积：mxn矩阵A和pxq的矩阵B：
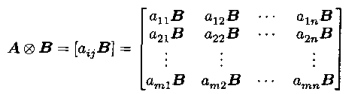
2）左Kronecker积：mxn矩阵A和pxq的矩阵B：
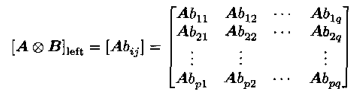
其中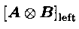
同样可以写为
。
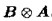七、矩阵梯度
一个基本形式是：
借助该形式，即可完成一般的梯度求解：
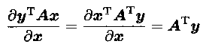
同时，结合梯度的四个基本法则，便可完成常用的梯度求解。
1）线性法则
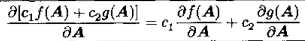
2）乘积法则
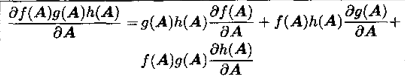
3）商法则
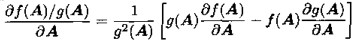
4）链式法则
