作者:桂。
时间:2017-03-17 12:18:15
链接:http://www.cnblogs.com/xingshansi/p/6557665.html

前言
本文为曲线与分布拟合一文的补充,由于混合分布的推导中用到EM算法,在此梳理一下。全文主要包括:
1)EM算法背景介绍;
2)EM算法原理推导;
3)EM应用
内容多有借鉴他人,最后一并附上链接。
一、背景介绍
A-硬币第一抛
本文以最大似然估计(MLE)为例(MAP等同样有效)。盒子里仅有硬币A,假设其正面出现的概率为$p$,并将出现正面记作1,反面记作0。进行$N$次独立重复试验(取$N=10$),
得到结果为:$y = ${1,1,0,1,0,0,1,1,1,1}。利用最大似然估计:
$Jleft( p ight) = mathop prod limits_{i = 1}^N {p^{{y_i}}}{left( {1 - p} ight)^{1 - {y_i}}} Rightarrow sumlimits_{i = 1}^N {{y_i}ln p + left( {1 - {y_i}} ight)} ln left( {1 - p} ight)$
将$y_i$的结果值代入,得:
$Lleft( p ight) = ln Jleft( p ight) = 7ln p + 3ln left( {1 - p} ight)$
求解:$p = frac{7}{10}$。
题外话:
MLE:所见即所得,$y_i = 1$个数为7,事实上统计概率$7/10$就是$p$的最佳估计。
MLE与熵(Entropy)同样存在联系,重写代价函数:
$Lleft( p ight) = ln Jleft( p ight) = 7ln p + 3ln left( {1 - p} ight)$
微调:
$Lleft( p ight) = ln Jleft( p ight) = 7/10ln p + 3/10ln left( {1 - p} ight) = qln p + left(1-q ight)ln left( {1 - p} ight)$
若要熵最大,有$q = p$,$p$为待估计的概率,$q$为统计概率0.7。
B-硬币第二抛
回到抛硬币的问题,接着抛硬币:盒子里仅有硬币B,假设其正面出现的概率为$s$,并将出现正面记作1,反面记作0,进行$N$次独立重复试验(取$N=10$),
得到结果为:$y = ${1,0,0,1,0,0,1,0,0,1}。利用最大似然估计,同样可以估计出:$s = 0.4$.
从这两次抛硬币来看,最大似然估计MLE都让问题得到解决。下面进行第三抛,MLE能否胜任呢?接着往下看。
C-硬币第三抛
可能是因为赶时间,这次拿出硬币就抛了,却没有留意硬币A、B都在盒子里!将出现正面记作1,反面记作0,进行$N$次独立重复试验(取$N=10$),得到观测结果为:$y = ${1,1,0,1,0,0,1,0,1,1},下面问题来了:根据观测数据$y$,分别估计A、B硬币正面的出现概率$p、s$?连哪一次是A、哪一次是B都不知道,怎么估计概率呢?MLE仍然不死心:假设A、B两枚硬币,拿出A的概率记为$pi$,拿出B的概率为$1-pi$,得到准则函数:
$Jleft( {pi,p,s} ight) = mathop prod limits_{i = 1}^N left[ {pi {p^{{y_i}}}{{left( {1 - p} ight)}^{1 - {y_i}}} + left( {1 - pi } ight){s^{{y_i}}}{{left( {1 - s} ight)}^{1 - {y_i}}}} ight]$
这个问题涉及三个未知参数$ heta = (pi,p,s)$,MLE强行优化准则:
$hat heta = arg mathop {max }limits_ heta log Jleft( {pi ,p,s} ight)$
再求偏导看看?MLE略显沮丧,EM走过来拍了拍他的肩膀:困难总会有解决办法,不是吗?
二、原理推导
A-算法步骤
硬币第三抛的问题可以简化为:
输入:观测变量数据Y,隐变量数据Z(可以将从盒中选A/B的概率看作是抛硬币Z决定,例如选硬币A的概率为$pi$,选硬币B的概率为$1-pi$,则等价为:抛硬币Z,正面则选择抛A,反面则选择抛B,且Z的正面概率为$pi$,反面概率为$1-pi$,由于观测不到Z,硬币Z就是隐变量数据。)联合分布P(Y,Z|$ heta$),条件分布P(Z,|Y,$ heta$);
输出:模型参数$ heta$.
对于输入模型,求解似然函数:
![]()
对于只有观测变量的情形(记为:完全数据情形),准则函数L借助MLE可解;但隐变量$Z$的存在(记为:缺失数据情形),$L( heta)$求解没有闭式解,但如果$P(Z| heta)$变为一个常数呢?即可将缺失数据情形转化为完全数据情形,从而借助MLE求解。按下面的步骤求解:
山寨版EM算法——
步骤1:给定一个初始值$P(Z| heta)$;
步骤2:利用MLE:对$L( heta)$求偏导,借助梯度下降求解$ heta$;
步骤3:再将求解的$ heta$看作常数,对$L( heta)$关于$P(Z| heta)$求解,得出新的$P(Z| heta)$估计;
步骤4:重复步骤1,直到满足收敛条件。
山寨版EM算法,利用了循环迭代的算法优化$L( heta)$,对数$log(.)$形式的求导造成分母有求和/积分项,可见即使转化为完全数据情形,求解也非常困难。
观察隐变量特性:通常$Z$一种取值决定了一组$ heta$,如$Z$取正面则观测数据影响$A$的概率求解,$Z$取反面则观测数据影响$B$的概率求解,如图所示:
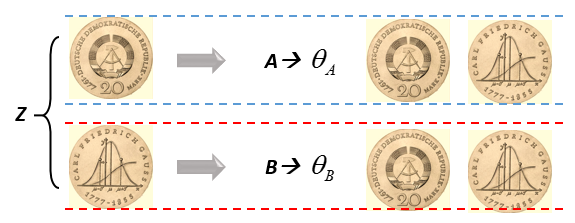
如果将 对数{关于Z求和}的形式,转换为 关于Z求和{对数}的形式,则针对每一种可能的Z求偏导便可以避免上述求解的麻烦,这是EM的关键所在。EM算法最大的特色不在于它可以对含有隐变量的问题进行估计,而在于:提供了一种近似$L( heta)$的准则函数$Q$,实现了求和与对数的转化,并证明了准则函数$Q$的有效性。
给出求解步骤:
正规版EM算法——
步骤1:选择参数的初值${ heta ^{left( 0 ight)}}$,开始迭代;
步骤2:E步(求$Qleft( heta , heta ^left( i ight) ight)$):记${ heta ^{left( i ight)}}$为第i次迭代参数$ heta$的估值,在第i+1次迭代的E步,计算:
其中,${Pleft( {Z|Y,{ heta ^{left( i ight)}}} ight)}$是给定观测数据Y和当前参数估计$ heta ^left( i ight)$下隐变量Z的条件概率分布。
事实上,E步主要求解隐变量条件概率密度$Pleft( {Z|Y,{ heta ^{left( i ight)}}} ight)$,这一步实现了缺失数据—>完全数据的转化,进而构造准则函数$Q$,为MLE求解参数(即M步)作准备;
步骤3:M步(在隐变量条件概率密度给定的前提下,利用MLE实现参数估计)求使$Qleft( { heta ,{ heta ^{left( i ight)}}} ight)$最大化的$ heta$,确定第$i+1$次迭代的参数的估计值${{ heta ^{left( {i + 1} ight)}}}$:
步骤4:重复步骤2、3,直到满足收敛条件。
EM算法的精华在于Q函数的给出,关于Q的来龙去脉,将在本文后半部分给出。
B-遗留问题求解
再回过头来看看MLE感到沮丧的问题——硬币第三抛。有了EM算法,我们来一步步分解这个问题。
记:观测数据为$Y$={$Y_1,Y_2,...Y_N$},对应隐变量为$Z$={$Z_1,Z_2,...Z_N$}。
- E-Step:
1)将缺失数据,转化为完全数据
假设已经得到第$i$次迭代的参数$ heta ^{left( i ight)}$,$ heta$ = {$pi,p,s$}.
E步的核心就是缺失数据到完全数据的转化,即计算条件概率$Pleft( {Z|Y,{ heta ^{left( i ight)}}} ight)$。
对于任意$Z_j$以及对应的$Y_j$,条件概率$Pleft( {Z_j|Y_j,{ heta ^{left( i ight)}}} ight)$有两种取值:
$Pleft( {{Z_j} = 1|{Y_j},{ heta ^{left( i ight)}}} ight)$
$Pleft( {{Z_j} = 0|{Y_j},{ heta ^{left( i ight)}}} ight)$
二者概率之和为1,故只计算其中一个即可,假设计算$Pleft( {{Z_j} = 1|{Y_j},{ heta ^{left( i ight)}}} ight)$。利用条件概率公式:
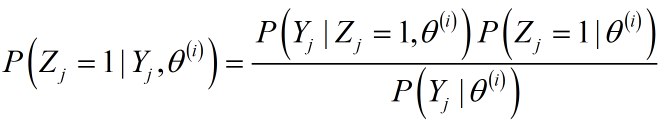
其中:
${Pleft( {{Z_j} = 1|{ heta ^{left( i ight)}}} ight)}$表示硬币Z第$j$次抛正面的概率,对应概率值为$pi^{(i)}$;
${Pleft( {{Y_j}|{Z_j} = 1,{ heta ^{left( i ight)}}} ight)}$表示硬币$Z$第$j$次抛正面时对应的$Y$的概率。Z抛正面对应选择硬币$A$,此时概率有两种可能:
| $Y_j = 0$ | $Y_j = 1$ |
| $p^{(i)}$ | $1-p^{(i)}$ |
${Pleft( {{Y_j}|{Z_j} = 1,{ heta ^{left( i ight)}}} ight)}$即为表格中的概率分布,简化成一个表达式:
![]()
分母为分子所有组合的求和。
硬币有两面,如果是3/4/..更多可能呢?事实上,每一个观测点可以表示为$Pleft( {{Z_j} in {Upsilon _k}|{Y_j},{ heta ^{left( i ight)}}} ight)$,${{Z_j} in {Upsilon _k}}$表示第$j$个观测点来自概率模型$k$,对应到这里就是:${Upsilon _1}$对应硬币正面,${Upsilon _2}$对应硬币反面,至于正面/反面记作0还是1或其他值,则无影响。
至此,完成了条件概率的求解,缺失数据变为完全数据。按照前文的分析,得到完全数据,对原始准则函数$L$求偏导亦可解。
但EM的精髓在于:将 $log[求和f(或积分)]$的形式转化为$求和(或积分)log(f)$的形式,简化求解。为此,我们需要写出新的准则函数Q。需要知道:L也好,Q也好,都是基于完全数据的求解,所以说条件概率的求解是E-step的核心。
2)构造准则函数Q
给出准则函数Q的固定形式:
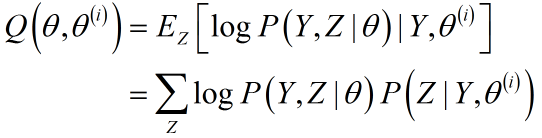
展开为具体形式:
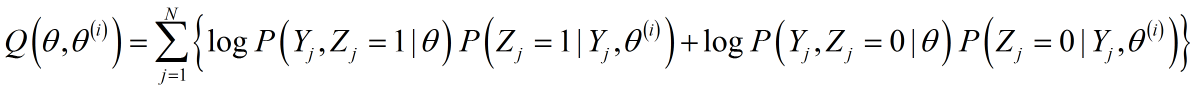
条件概率已经求出,又${log Pleft( {{Y_j},{Z_j} = 0| heta } ight)}$同${log Pleft( {{Y_j},{Z_j} = 1| heta } ight)}$一样,在求解条件概率的中间过程已经求出(上文有对应公式,不过注意$log(.)$的参数是$ heta$,而不是$ heta^{(i)}$),再次印证一点:E-Step重要的是条件概率的求解,一旦求解得出,就会有两件事发生:1)缺失数据变为完全数据;2)Q函数可直接给出;
硬币第三抛对应的Q函数:
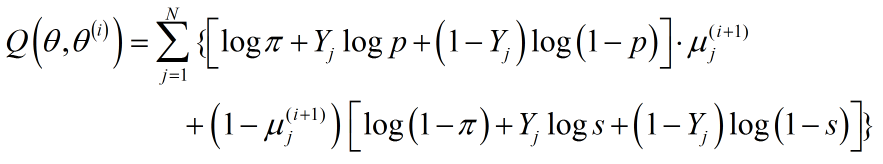
其中$mu _j^{(i + 1)}$:
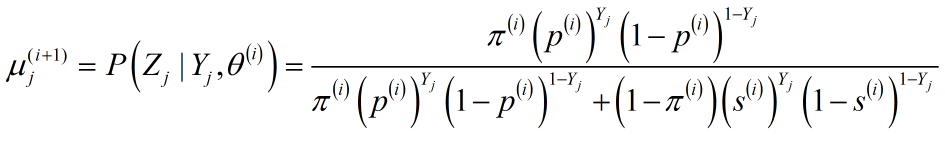
- M-Step:
1)利用MLE求解参数
有了Q函数,利用MLE分别求偏导:

至此,EM算法完成求解,MLE笑从双脸生。
C-算法推导
1)凸函数

粗略翻译:
$f$是定义域为实数的函数,如果$x$是实数,满足$f^{''} ge 0$;如果$x$为向量,满足Hessian矩阵$H ge 0$;这两种情况下$f$为凸函数,当不取等号时,$f$为严格凸函数。
2)Jensen不等式

粗略翻译:
$f$是凸函数,且$X$为随机变量,则:
$Eleft( {fleft( X ight)} ight) ge fleft( {Eleft( X ight)} ight)$
若$f$是严格凸函数,当且仅当$P(X = E(X)) = 1$时上式等号成立(此时,$X$为一常数)。
示意图:
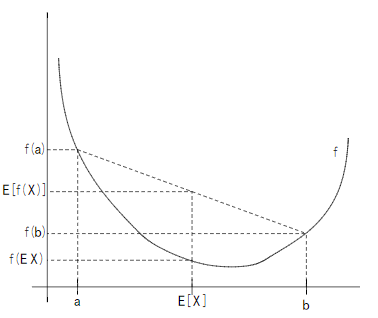
下面我们证明一下Jensen不等式:
假设$f$为凸函数,且区间为$I$,有${x_1},{x_2},...,{x_n} in I$,对应概率密度为${p_1},{p_2},...,{p_n}$,且$sumlimits_{i = 1}^n {{p_i}} = 1$。利用数学归纳法加以证明。
$n=1$没有讨论的意义;当$n=2$,对应凸函数定义,故结论显然成立;
假设不等式对$n=K$有效,当$n=K+1$时,
至此,Jensen不等式得证。
另外,当$f$为凹函数时,$-f$为凸函数。
3)Q函数推导
再次给出准则函数L:
![]()
考虑到:1)构造均值形式,需添加概率密度;2)构造完全数据,需要得出在给定$ heta^{(i)},Y$下的$Z$估计,针对L利用Jensen不等式:
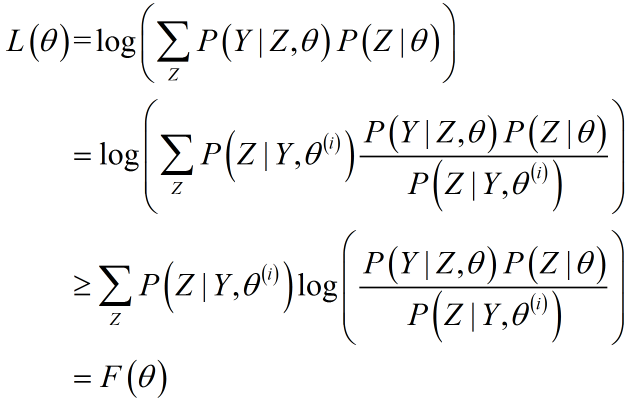
$log$是严格凸函数,故在$ heta = heta^{(i)}$处,$F( heta) = L( heta)$.即$F( heta)$是$L( heta)$的下界,给出示意图(B就是F,严格意义上$F( heta)$记作$F( heta, heta^{(i)})$):
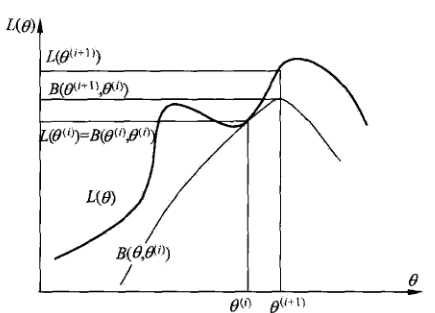
借助$F( heta)$的性质,有了EM的思路:
- (E-Step)通过给定的$ heta^{(i)}$,求出隐变量条件概率,形成完全数据;
- (M-Step)利用完全数据,对$F( heta, heta^{(i)})$进行MLE求参;
对$F( heta)$利用MLE求参时:
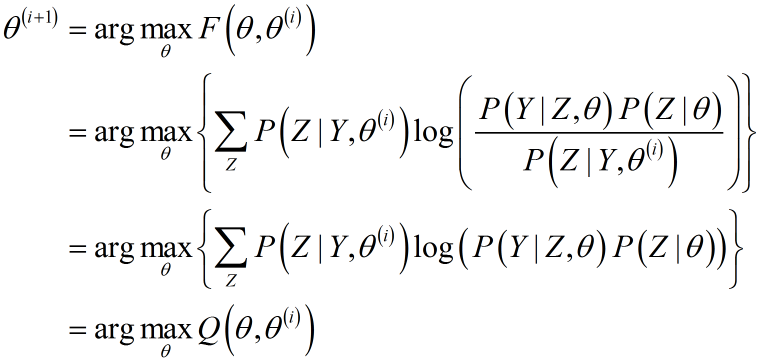
这就是Q函数的由来。
关于收敛性证明,可以参考李航博士《统计学习方法》P160~162.
三、应用举例
限于篇幅,拟单独写几篇文章并配合代码理理EM算法,内容包括:
参考:
李航《统计学习方法》;
Andrew Ng:CS229 Lecture notes.