一篇文章帮你搞懂二叉堆的那些事

【系列文章推荐阅读】

• 【数据结构之顺序表】用图和代码让你搞懂顺序结构线性表
• 【数据结构之链表】看完这篇文章我终于搞懂链表了
• 【数据结构之栈】用详细图文把「栈」搞明白（原理篇）
• 【数据结构之队列】详细图解！在学习队列？看这一篇就够了！
• 【数据结构之链表】详细图文教你花样玩链表
• 【数据结构之二叉树】一文看懂二叉树的概念和原理
• 【数据结构之二叉树】二叉树的创建及遍历实现
• 【数据结构之线索二叉树】线索二叉树的原理及创建

1. 什么是二叉堆？

“二叉”自不必多说，本章主要介绍的树都是二叉树。那么啥是“堆”呢？

我们在日常生活中，通常会说“一堆东西”或者“堆东西”，这里的“堆”，通常指重叠放置的许多东西。

我们在堆东西的时候，肯定都有一个经验，即：为了使这堆东西更稳定，会将比较重的、大的东西放在下面，比较轻的、小的东西放在上面。

这个经验放在数据结构——二叉树中，同样适用。只不过“重”“大”是根据结点值的大小来判断的，并且是在双亲结点和孩子结点之间进行比较的。

比如，结点值大的，作为孩子结点；结点值小的，作为双亲结点。

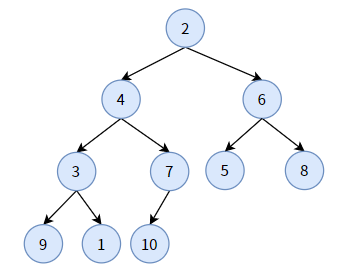
下面举一个例子，先看下面一颗普通二叉树，也是一颗完全二叉树：

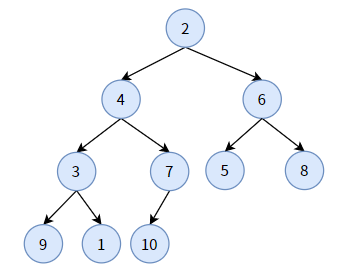
再看下面一颗二叉堆：

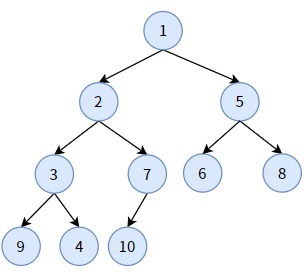
这个二叉堆的特点是：

• 它是一颗完全二叉树。事实上，该二叉堆就是由上图的完全二叉树经过调整转化而来；
• 任何一个双亲结点的值，均小于或等于左孩子和右孩子的值；
• 每条分支从根结点开始都是升序排序（如分支 1-2-3-4）。

这样的二叉堆被称为最小堆，它的堆顶，即根结点 A，是整棵树的最小值。

与最小堆相对应的是最大堆：

• 最大堆是一颗完全二叉树；
• 它的任何一个双亲结点的值，均大于或等于左孩子和右孩子的值；
• 每条分支从根结点开始都是降序排序。

最大堆的堆顶，是整棵树的最大值。

我们将上图中的普通二叉树转化为最大堆，如下图：

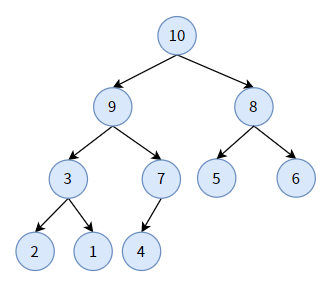
2. 二叉堆的操作

2.1. 构造二叉堆

给你一颗完全二叉树，如何调整结点，构造出一个二叉堆？下面是一颗无序的完全二叉树：

现在我们想要构造出一个最小堆，首先找到这颗完全二叉树中所有的非叶子结点（绿色标记）：

我们要做的事是：对每个非叶子结点，做最小堆的“下沉”调整。

何谓最小堆的“下沉”调整？

对某个非叶子结点，如果该结点大于其孩子结点中最小的那个，则交换二者位置，否则不用交换。在图上则表现出非叶子结点（即大值结点）“下沉”一个层次。运动是相对的，大值结点“下沉”，就相当于小值结点“上浮”。

需要注意的是，有时下沉一次是不够的，我们需要下沉多次，确保该结点下沉到底（即它不再大于其孩子）。

所有非叶子结点，从最后一个开始，按照从右到左，从下到上的顺序进行多次最小堆的下沉调整，即可构造成最小堆。

比如对于值为 4 的非叶子结点而言，它下沉到第 3 层次后，仍然大于其孩子，这不算“下沉到底”，还需要继续下沉到第 4 层次。至此，在分支 2-4-3-1 上，“大值”结点 4 算是下沉到底了。

下面进行分步解释：

1. 对非叶子结点 7，它小于其孩子结点 10， 不用“下沉”；

   

2. 对非叶子结点 3，它大于其孩子结点中较大的结点 1，结点 3 要“下沉”，和结点 1 交换。显然，结点 3 沉到底了。

   

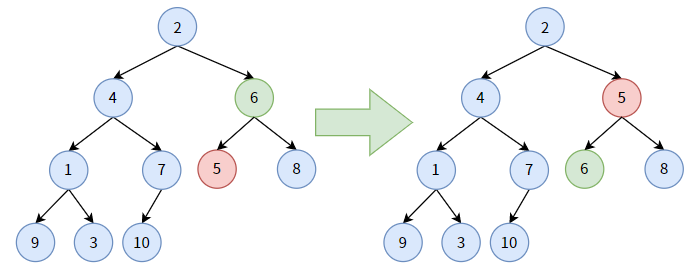
3. 对非叶子结点 6，它大于其孩子结点中较小的结点 5，结点 6 要“下沉”， 和结点 5 交换位置。显然，结点 6 沉到底了。

   

4. 对非叶子结点 4，它大于其孩子结点中最小的结点 1，结点 4 要 “下沉”，和结点 1 交换位置。显然，结点 4 并未沉到底。

   

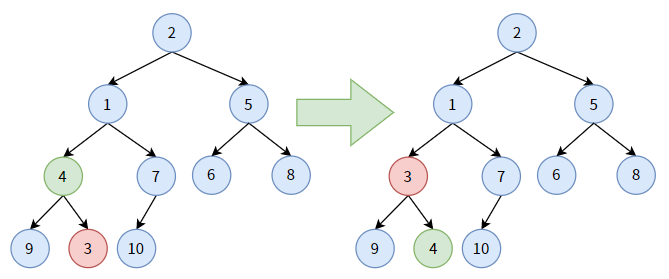
5. 仍对结点 4，它大于其孩子结点中最小的结点 3，结点 4 要“下沉”， 和结点 3 交换位置。此时，结点 4 算是沉底了。

   

6. 对非叶子结点 2，它大于其孩子结点中最小的结点 1，结点 2 要“下沉”，和结点 1 交换位置。显然，结点 2 算是沉到底了。

   

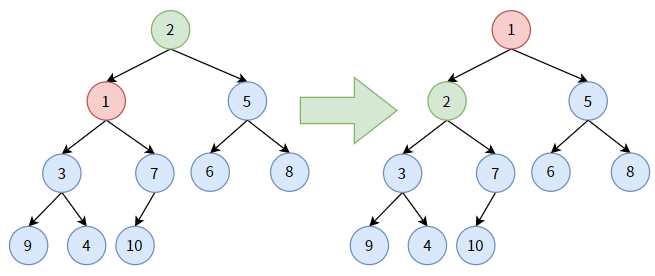
至此，我们将一颗无序的完全二叉树调整改造成了最小二叉堆，你可以检查一下，最小堆中的所有结点皆满足双亲的值小于孩子的值。并且，5 条分支上都是有序的。

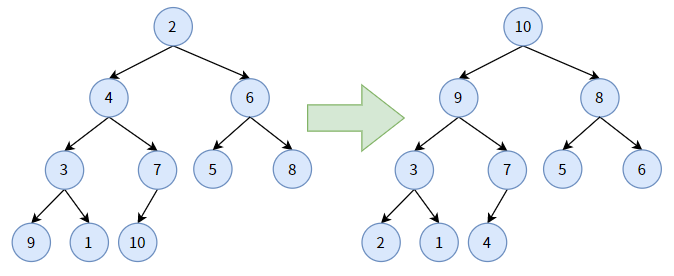
构造最大堆的步骤类似，不过最大堆的下沉调整是：如果某结点小于其孩子结点中最大的那个，则交换二者位置，在图上表现为非叶子结点（即小值结点）“下沉”一个层次。通过多次下沉调整，使该结点不再小于其孩子。

下图把一个无序完全二叉树调成为最大堆：

2.2. 插入结点

二叉堆是一个完全二叉树，要向其中插入结点，插入到完全二叉树的最后一个结点的下一个位置即可。

比如向下面的一个最大堆中插入结点 11，要插到最后一个结点 4 的下一个位置。当最大堆新插入一个结点 11 时，它就不再是最大堆了，因为结点 11 破坏了原堆的结构。所以，我们应当将其看作一个新的完全二叉树，然后调整新完全二叉树再次构造出最大堆。（调整过程见上）

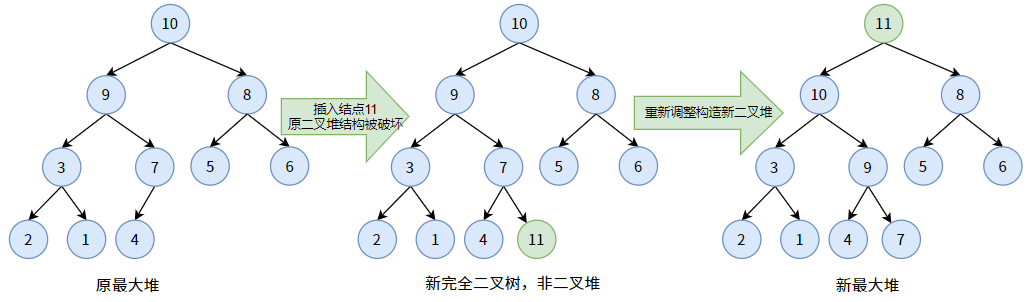
2.3. 删除结点

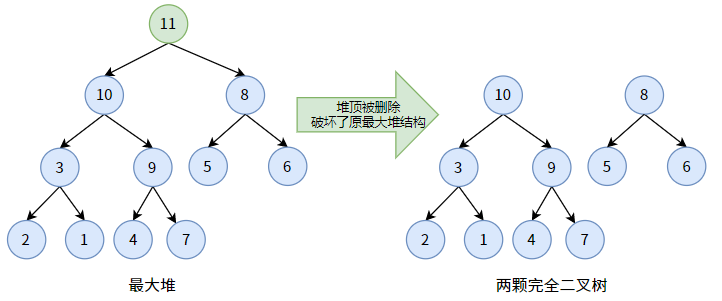
删除操作与插入操作相反，是删除第一个位置的元素，即删除堆顶。

我们以删除上图最大堆的堆顶 11 为例。

当删除堆顶 11 后，二叉堆原结构被破坏，甚至不是一颗二叉树了（变成两颗）：

为了保持完全二叉树的形态，我们把最后一个结点 7 补到根结点去，顶替被删除的根结点 11。如此一来，我们又得到了一个新完全二叉树（不是二叉堆），然后我们根据这颗新完全二叉树再次构造出最大堆即可。

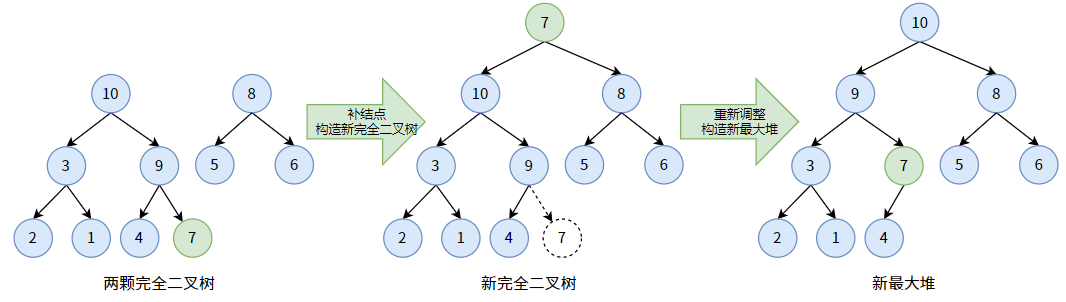
3. 二叉堆的存储结构

二叉堆的存储结构是顺序存储，因为二叉堆是一颗完全二叉树，在文章【二叉树的存储】中我们说过：完全二叉树适合使用顺序存储结构来实现。

下图是一个最大堆，红色方框是对结点的编号，和数组下标一一对应。

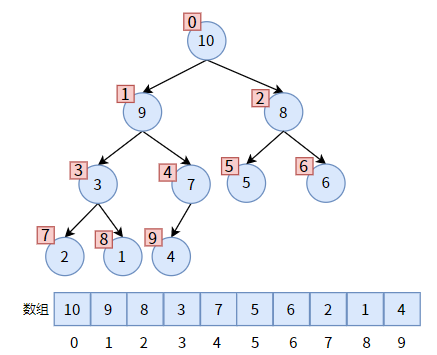
链式存储结构能够清晰而形象地为我们展现出二叉堆中双亲结点和左右孩子的关系。但是数组中没有指针，只有数组下标，怎么表示双亲和孩子的关系呢？

其实对于完全二叉树来说，数组下标足矣！

现假设二叉堆中双亲结点的数组下标为 parent_index，左孩子的数组下标为 left_child_index，右孩子的数组下标为 right_child_index，那么它们之间有如下关系：

（一）left_child_index = 2 × parent_index + 1

（二）right_child_index = 2 × parent_index + 2

（三）parent_index = (left_child_index - 1) ÷ 2

（四）parent_index = (right_child_index - 2) ÷ 2

（五）right_child_index = left_child_index + 1

比如：结点 3 的下标为 3 ，则其左孩子 2 的下标为 2 × 3 + 1 = 7、右孩子 1 的下标为 2 × 3 + 2 = 8；

结点 3 的下标为 3，作为左孩子，其双亲下标为 (3 - 1) ÷ 2 = 1；结点 7 的下标为 4，作为右孩子，其双亲下标为 (4 - 2) ÷ 2 = 1；

假设某结点的数组下标为 child_index，你不知道该结点是左孩子还是右孩子，要求其双亲的下标，有

（六）parent_index = (child_index - 1) ÷ 2

比如：你不知道结点 5（下标为 5）、结点 6（下标为 6）是左孩子还是右孩子，则结点 5 和结点 6 的双亲下标分别为 (5 - 1) ÷ 2 = 2 、(6 - 1) ÷ 2 = 2。（注意，编程语言中的整型运算，所以结果不是小数）

这里，我们使用结构体实现二叉堆：

#define MAXSIZE 20 // 数组的最大存储空间

typedef struct {
    int array[MAXSIZE]; // 存储数组
    int length; // 当前堆长度（结点数）
} BinaryHeap;

在进行实际操作之前，需要初始化二叉堆，即对数组及堆长度赋值：

/**
 * @description: 初始化二叉堆
 * @param {BinaryHeap} *heap 二叉堆
 * @param {int} *array 数组首地址，该数组是一个无序完全二叉树
 * @param {int} arr_length 数组长度
 * @return {*} 无
 */
void init_heap(BinaryHeap *heap, int *array, int arr_length)
{
    // array 拷贝到 heap 中
    memcpy(heap->array, array, arr_length * sizeof(int));
    // 设置堆长度
    heap->length = arr_length;
}

4. 二叉堆的具体实现

4.1. 调整和构造

这里以构造最小堆为例。

要构造一个最小堆，就得调整所有的非叶子结点。而调整的依据就是比较非叶子结点和其孩子的大小。

我们约定 parent 为非叶子结点， parent_index 为其下标。child 为其孩子中较小的那个，child_index为其下标。

child 开始默认标识左孩子，那么右孩子的下标即为 child_index + 1。当左孩子小于等于右孩子时，child 不需要改变；当左孩子大于右孩子时，就得更新 child_index ，使child 标识右孩子。

下面结合下图中值为 4 的非叶子结点为例，讲述代码如何实现。

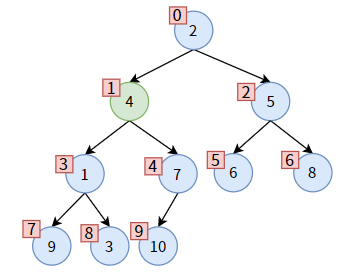
先比较 parent 的左右孩子，左孩子较小，则 child 为左孩子，不需要更新 child_index。

parent 和 child 各就各位，发现 parent 大于 child，可以交换位置。在交换之前，先保存一下 parent 的值，即 parent_value = 4：

交换位置：先把 child的值赋给 parent，从而达到 值1 上浮的效果：

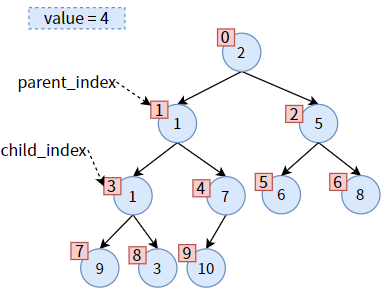
然后更新 parent_index 和 child_index，二者都往下走一层次：

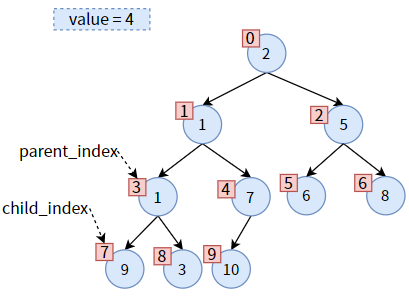
然后将之前保存的 value 赋给现在的 parent，从而达到 值4 下沉的效果：

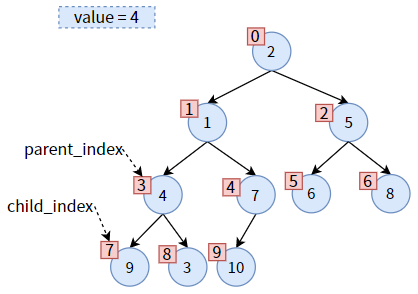
一次调整完成，但对于 值4 来说，并没有结束，因为 值4 还没有沉到底。

比较此时 parent 的左右孩子，发现右孩子较小，则 child 为右子树，需要更新 child_index，使 child 标识右孩子：

现在可以交换位置了，把 child 的值赋给 parent，达到 值3 的上浮：

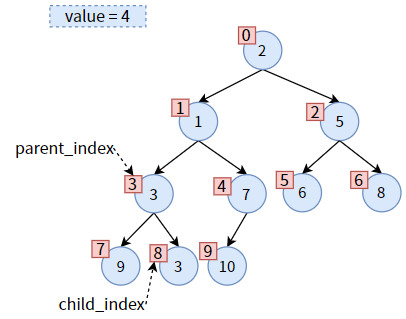
然后，更新 parent_index 和 child_index 的值，二者向下走一个层次：

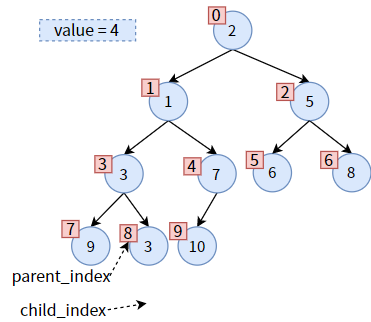
把 value 赋给 parent，达到 值4 的下沉：

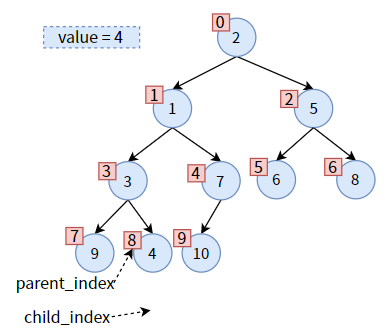
此时，child_index 已超过了二叉堆的长度，即 值4 已经到底了。

调整代码如下：

/**
 * @description: 针对某个非叶子结点进行到底的下沉调整
 * @param {BinaryHeap} *heap 二叉堆（无序）
 * @param {int} parent_index 某个非叶子结点
 * @return {*} 无
 */
void adjust_for_min_heap(BinaryHeap *heap, int parent_index)
{
    // value 保存非叶子结点的值
    int value = heap->array[parent_index];
    // child_index 标识左孩子
    int child_index = parent_index * 2 + 1;
    // 最后一个结点的下标
    int last_child_index = heap->length - 1;

    // 双亲结点 parent 至少有一个孩子
    while (child_index <= last_child_index) {
        // 如果双亲结点 parent 有左孩子和右孩子
        if (child_index < last_child_index) {
            // 比较左孩子和右孩子谁小，如果右孩子小，
            if (heap->array[child_index] > heap->array[child_index + 1]) {
                // 则 child_index 标识右孩子
                child_index = child_index + 1;
            }
        }
        // 如果双亲的值大于 child 的值
        if (value > heap->array[child_index]) {
            heap->array[parent_index] = heap->array[child_index]; // 小节点上浮
            parent_index = child_index; // 更新双亲下标
            child_index = parent_index * 2 + 1; // 更新孩子下标
        } else { // 不做操作，跳出循环
            break;
        }
        // 大节点下沉
        heap->array[parent_index] = value;
    }
}

构造代码如下：

/**
 * @description: 构造最小堆
 * @param {BinaryHeap} *heap 二叉堆（无序）
 * @return {*} 无
 */
void create_min_heap(BinaryHeap *heap)
{
    // 每个非叶子结点都调整
    for (int i = (heap->length - 2) / 2; i >= 0; i--) {
        adjust_for_min_heap(heap, i);
    }
}

4.2. 插入结点

只需将新结点插入二叉堆最后一个结点的下一个位置，然后重新构造二叉堆。

以最小堆为例，代码如下：

/**
 * @description: 向最小堆中插入一个元素
 * @param {BinaryHeap} *heap 最小堆指针
 * @param {int} elem 新元素
 * @return {*} 无
 */
void insert_into_min_heap(BinaryHeap *heap, int elem)
{
    if (heap->length == MAXSIZE) {
        printf("二叉堆已满，无法插入。
");
        return;
    }
    heap->array[heap->length] = elem; // 插入
    heap->length++; // 更新长度
    create_min_heap(heap); // 重新构造
}

4.3. 删除结点

将最后一个结点移动（赋值）到堆顶，然后重新构造二叉堆。

以最小堆为例，代码如下：

/**
 * @description: 删除最小堆的堆顶
 * @param {BinaryHeap} *heap 最小堆指针
 * @param {int} *elem 保存变量指针
 * @return {*} 无
 */
void delete_from_min_heap(BinaryHeap *heap, int *elem)
{
    if (heap->length == 0) {
        printf("二叉堆空，无元素可删。
");
        return;
    }
    *elem = heap->array[0];
    heap->array[0] = heap->array[heap->length - 1]; // 移动到堆顶
    heap->length--; // 更新长度
    create_min_heap(heap); //重新构造
}

5. 总结

构造最大堆的本质是：将每颗子树的“大”结点上浮作为双亲，“小”结点下沉作为孩子。

构造最小堆的本质是：将每颗子树的“小”结点上浮作为双亲，“大”结点下沉作为孩子。

插入结点的本质是：插入新结点至二叉堆末尾，破坏了原二叉堆的结构，然后调整新得到的完全二叉树，重新构造二叉堆。

删除结点的本质是：删除堆顶，破坏了原完全二叉树的结构，然后使用最后一个结点，重新构造完全二叉树，再调整新得到的完全二叉树，重新构造二叉堆。

用四个字概括就是——破而后立。

至于代码实现，关键在于结点的调整，把这个搞明白，剩下的就简单了。

以上就是二叉堆的原理和相关操作。

完整代码请移步至 GitHub | Gitee 获取。

如有错误，还请指正。

如果觉得写的不错，可以点个赞和关注。后续会有更多数据结构和算法相关文章。