1.平稳的时间序列
级数的平均值不应是时间的函数,而应是常数;
系列的方差不应该是时间的函数,该特性被称为同调;
第i项和第(i + m)项的协方差不应该是时间的函数。
除非时间序列稳定,否则将无法建立时间序列模型。在违反固定标准的情况下,首要条件是使时间序列平稳,然后尝试使用随机模型预测该时间序列。带来这种平稳性的方法有多种。其中一些是趋势消除,差异化等。
2.随机漫步(小女孩走象棋)
X(t)= X(0)+ Sum(Er(1),Er(2),Er(3)..... Er(t))
Er(t)是时间点t的误差。这是女孩在每个时间点带来的随机性。
随机游走不是平稳过程,因为它具有时变方差。另外,如果我们检查协方差,我们会发现它也取决于时间。
平均数是常数。方差取决于时间。协方差也取决于时间。
随机游走不是平稳过程。
3.加入Rho
X(t)= Rho * X(t-1)+ Er(t)
rho = 1成为在固定测试中表现不佳的特殊情况
4.Dickey Fuller平稳性测试
X(t)-X(t-1)=(Rho-1)X(t-1)+ Er(t)
测试Rho – 1是否显着不同于零。如果原假设被拒绝,我们将得到一个平稳的时间序列。
5.在ARMA模型中,AR代表自回归,MA代表移动平均,AR或MA不适用于非平稳序列。
如果您得到一个非平稳序列,则首先需要使序列平稳(通过进行差分/变换),然后从可用的时间序列模型中进行选择。
AR
国家GDP x(t)= alpha * x(t – 1)+误差(t)
数字(1)表示下一个实例仅取决于前一个实例。alpha是我们寻求的,以使误差函数最小化的系数。注意,x(t-1)确实以相同的方式链接到x(t-2)。因此,对x(t)的任何冲击在将来都会逐渐消失。
MA
商品袋子 x(t)= beta *错误(t-1)+错误(t)
在MA模型中,噪音/冲击会随着时间迅速消失。AR模型具有震荡的持久效果。
6.AR和MA模型之间的主要区别是基于不同时间点的时间序列对象之间的相关性。
对于n> MA的阶数,x(t)和x(tn)之间的相关性始终为零。这直接源自以下事实:对于MA模型,x(t)和x(tn)之间的协方差为零
。但是,在AR模型中,随着n变大,x(t)和x(tn)的相关性逐渐下降。无论具有AR模型还是MA模型,都可以利用此差异。
相关图可以给我们MA模型的顺序。
7.
获得平稳的时间序列后,我们必须回答两个主要问题:
Q1。是AR还是MA流程?
Q2。我们需要使用什么顺序的AR或MA流程?
第一个问题可以使用总相关图(也称为自动相关函数/ ACF)来回答。ACF是不同滞后函数之间的总相关性图。例如,在GDP问题中,时间点t的GDP为x(t)。我们对x(t)与x(t-1),x(t-2)的相关性感兴趣。现在,让我们来反思一下我们上面学到的东西。
在滞后n的移动平均值序列中,我们将不会获得x(t)和x(t – n -1)之间的任何相关性。因此,总相关图在第n个滞后处截止。因此,找到MA系列的滞后变得简单。对于AR系列,此相关性将逐渐下降而没有任何截止值。那么,如果它是AR系列,我们该怎么办?
这是第二招。如果我们发现每个滞后的偏相关性,它将在AR级数之后被截断。例如,如果我们有一个AR(1)系列,如果排除第一滞后(x(t-1))的影响,那么第二滞后(x(t-2))与x(t)无关。因此,部分相关函数(PACF)将在第一个滞后后急剧下降。
PACF曲线截止,这意味着这主要是一个AR(2)过程。
ACF曲线截止,这意味着这主要是一个MA(2)过程。
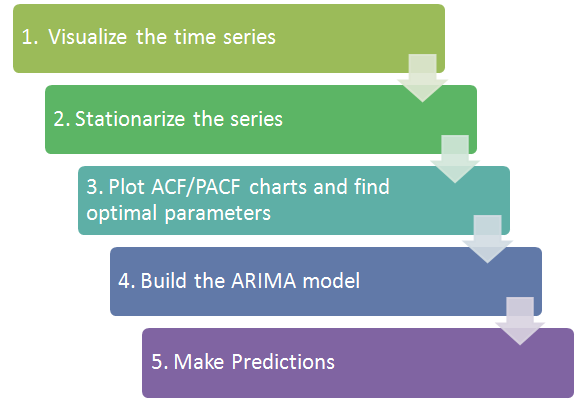
步骤1:可视化时间序列
在建立任何类型的时间序列模型之前,必须分析趋势。我们感兴趣的细节与该系列中的任何趋势,季节性或随机行为有关。
步骤2:平稳化系列
一旦知道了模式,趋势,周期和季节性,就可以检查序列是否稳定。迪基-富勒(Dickey-Fuller)是一项流行的测试之一。如果发现该系列不平稳怎么办?
有三种常用的技术可以使时间序列平稳:
1.去 趋势:在这里,我们只是从时间序列中删除趋势成分。例如,我的时间序列的等式是:
x(t)=(平均值+趋势* t)+误差
我们将简单地删除括号中的部分,并为其余部分构建模型。
2. 差异:这是消除不稳定性的常用技术。在这里,我们尝试对术语而非实际术语的差异进行建模。例如,
x(t)– x(t-1)= ARMA(p,q)
这种差异称为AR(I)MA中的集成部分。现在,我们有三个参数
p:AR
d:我
q:马
3. 季节性:季节性可以轻松地直接合并到ARIMA模型中。
步骤3:找出最佳参数
可以使用ACF和PACF图找到参数p,d,q 。如果ACF和PACF都逐渐减小,则可以添加此方法,这表明我们需要使时间序列平稳并将值引入“ d”。
步骤4:建立ARIMA模型
有了参数,我们现在可以尝试构建ARIMA模型。上一节中找到的值可能是一个近似估计值,我们需要探索更多(p,d,q)组合。BIC和AIC最低的那个应该是我们的选择。我们也可以尝试一些具有季节性成分的模型。为了以防万一,我们注意到ACF / PACF图中有任何季节性。
步骤5:做出预测
一旦有了最终的ARIMA模型,我们现在就可以对未来的时间点进行预测了。如果模型运行良好,我们还可以可视化趋势进行交叉验证。
学习小结:
时间序列必须平稳,这个可以通过做图扽方式查看,检验是否平稳(Dickey-Fuller测试),如果不是则需要平稳化,比如去趋势、差异(也就是差分选p d q这些)、季节性
利用ACF和PACF图分别寻找参数(也就是看两个图中什么时候截断,换句话说就是什么时候平稳下来)再建立p d q下的a ri ma模型,然后就可以预测了。
在接下来的一章节中,再去结合https://blog.csdn.net/orDream/article/details/100013682,我们才会发现 :时间序列真香!
具体内容请参照文末链接自行学习,如有不解之处欢迎在下方评论区讨论
参考https://www.analyticsvidhya.com/blog/2015/12/complete-tutorial-time-series-modeling/